Springe zum Inhalt oder Footer
SerloDie freie Lernplattform

Pyramide

Eine Pyramide ist ein Körper, der durch Verbinden aller Ecken eines beliebigen Vielecks mit einem Punkt außerhalb der Ebene, in der das Vieleck liegt, entsteht.

Cheops-Pyramide

Cheops-Pyramide

Volumen

VPyramide=13⋅G⋅hV_\text{Pyramide} = \frac{1}{3}\cdot G \cdot h

G: Grundfläche

h: Höhe

Pyramide mit Bezeichnungen

Oberflächeninhalt

OPyramide\displaystyle O_{\text{Pyramide}}==G+M\displaystyle G + M
==a2+4⋅a⋅ha2\displaystyle a^2+4\cdot\dfrac{a\cdot h_a}{2}
==a2+2⋅a⋅ha\displaystyle a^2+2\cdot a\cdot h_a
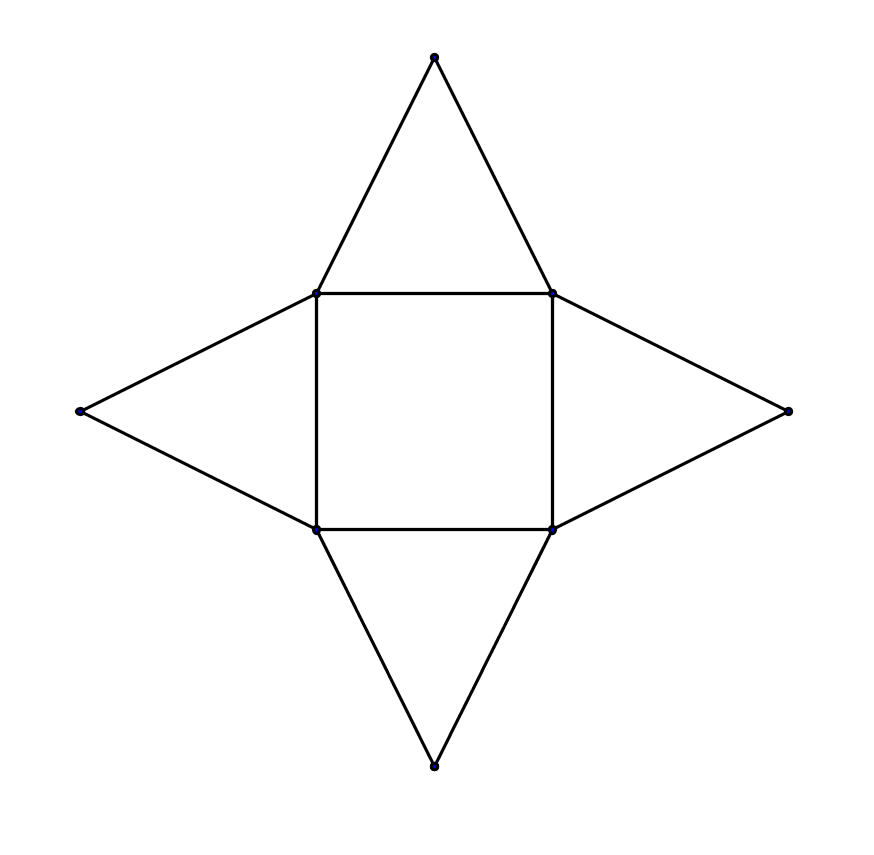
Netz vierseitige Pyramide

Die Grundfläche GG ist ein Vieleck, hier ein Quadrat.

Die Mantelfläche MM besteht aus den Seitenflächen, hier aus vier Dreiecken.

Weitere Formeln für Berechnungen an einer geraden, regelmäßigen Pyramide mit quadratischer Grundfläche

Grundfläche

Diagonale d:

Pythagoras im rechtwinkligen Dreieck:

d2\displaystyle d^2==a2+a2\displaystyle a^2+a^2
==2⋅a2\displaystyle 2\cdot a^2
↓

Wurzel auf beiden Seiten ziehen

d\displaystyle d==2⋅a\displaystyle \sqrt{2}\cdot a
Grundfläche mit Diagonale

Seitenfläche

Höhe eines Dreiecks hah_a:

Betrachte einen Ausschnitt aus dem obigen Pyramidenbild, der die Dreieckshöhe hah_a enthält.

Pythagoras im rechtwinkligen Dreieck:

ha2\displaystyle h_a^2==(a2)2+h2\displaystyle (\frac{a}{2})^2+h^2
↓

Wurzel auf beiden Seiten ziehen

ha\displaystyle h_a==(a2)2+h2\displaystyle \sqrt{(\frac{a}{2})^2+h^2}
Dreieck mit Seitenhöhe h_a

Seitenfläche

Seitenkante s:

(Möglichkeit 1 für die Berechnung)

Betrachte einen Ausschnitt aus dem obigen Pyramidenbild, der die Seitenkante ss und die Dreieckshöhe hah_a enthält.

Pythagoras im rechtwinkligen Dreieck:

s2\displaystyle s^2==(a2)2+ha2\displaystyle (\frac{a}{2})^2+h_a^2
↓

Wurzel auf beiden Seiten ziehen

s\displaystyle s==(a2)2+ha2\displaystyle \sqrt{(\frac{a}{2})^2+h_a^2}
Dreieck mit Seitenkante und Höhe

Seitenfläche

Seitenkante s:

(Möglichkeit 2 für die Berechnung)

Betrachte einen Ausschnitt aus dem obigen Pyramidenbild, der die Seitenkante ss und die Pyramidenhöhe hh enthält.

Pythagoras im rechtwinkligen Dreieck:

s2\displaystyle s^2==(d2)2+h2\displaystyle (\frac{d}{2})^2+h^2\displaystyle
↓

Wurzel auf beiden Seiten ziehen

s\displaystyle s==(d2)2+h2\displaystyle \sqrt{(\frac{d}{2})^2+h^2}
Dreieck mit Seitenkante und Höhe h

Video zum Thema Oberfläche und Volumen der Pyramide

Sonderformen der Pyramide

Bezeichnungen

Eigenschaften

Beispiele

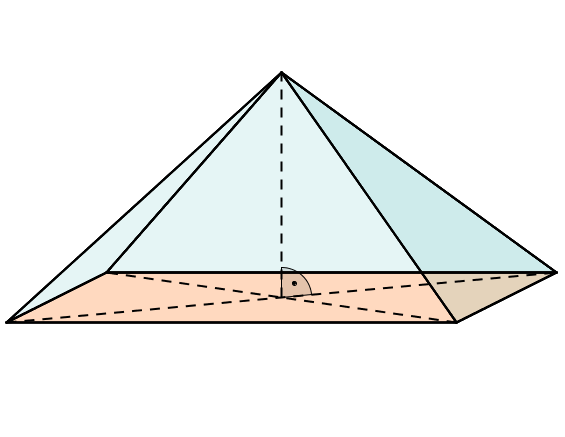
gerade Pyramide

  • alle Kanten der Mantelflächen sind gleich lang

  • die Spitze der Pyramide liegt senkkrecht über den Mittelpunkt der Grundfläche

Bild

regelmäßige/reguläre Pyramide

  • gerade Pyramide mit regelmäßigem Vieleck als Grundfläche

Bild

Bild

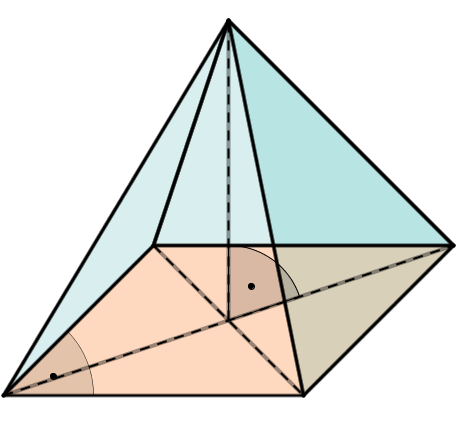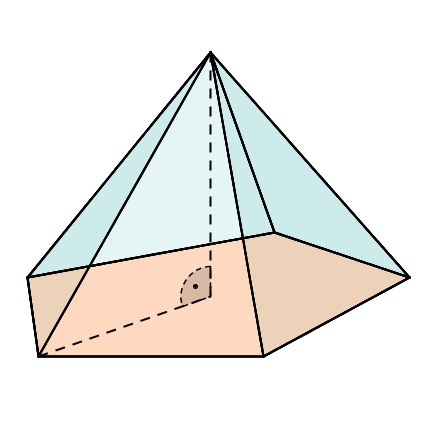schiefe Pyramide

  • Die Spitze liegt nicht genau über dem Mittelpunkt der Grundfläche.

  • Sie hat das gleiche Volumen wie die gerade Pyramide mit gleicher Höhe

Bild

regulärer Tetraeder

Pyramide, die

  • vier kongruente gleichseitige Dreicke als Fläche hat

  • sechs gleich lange Kanten hat

Bild
Merke

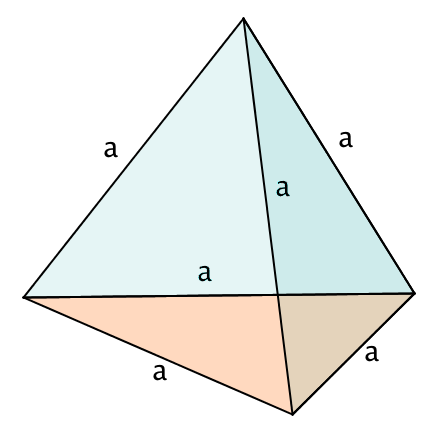Jede regelmäßige Pyramide ist eine gerade Pyramide. Die Umkehrung dieser Aussage ist nicht in jedem Fall richtig. Es gibt also gerade Pyramiden, die nicht regelmäßig sind (z.B. eine vierseitige Pyramide mit rechteckiger Grundfläche).

Berechnen des Volumens anderer Körper   

Im Artikel Volumenberechnung in der analytischen Geometrie findet man eine fortgeschrittenere Variante für die Berechnung des Volumens einer Pyramide. Auch das Volumen anderer Körper wird dort berechnet.

Übungsaufgaben: Pyramide

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel


Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?