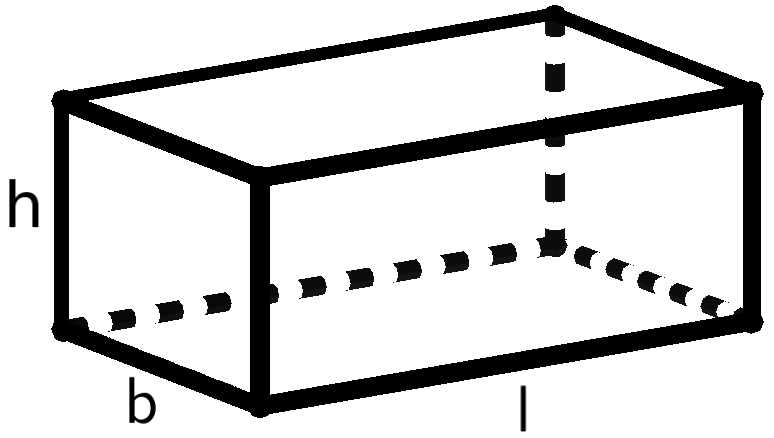
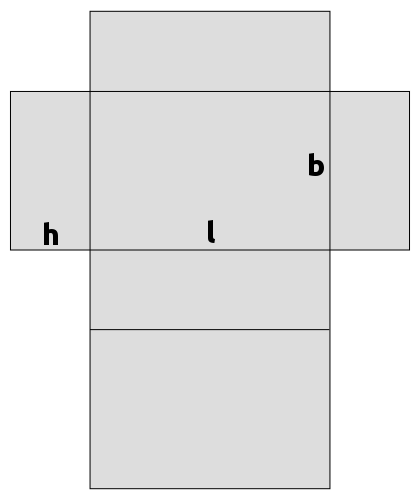
Alle Flächen eines Körpers zusammen bezeichnet man als die Oberfläche. Bei manchen Körpern (zum Beispiel bei Kegeln oder Zylindern) unterteilt man sie noch in Grundfläche und Mantelfläche.
Quader
Prisma
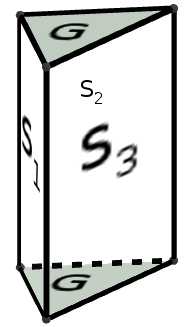
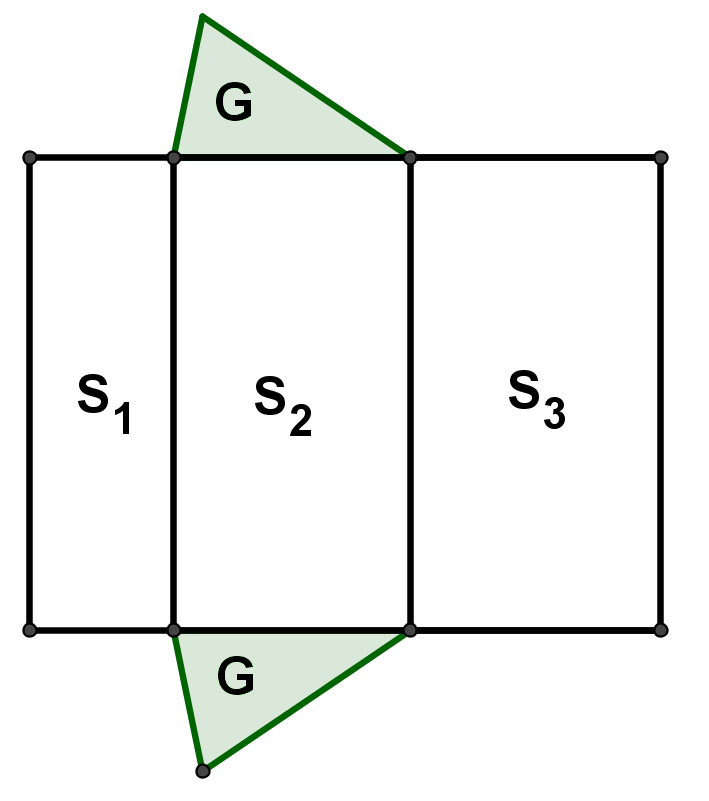
Netz des Prismas:
Zylinder
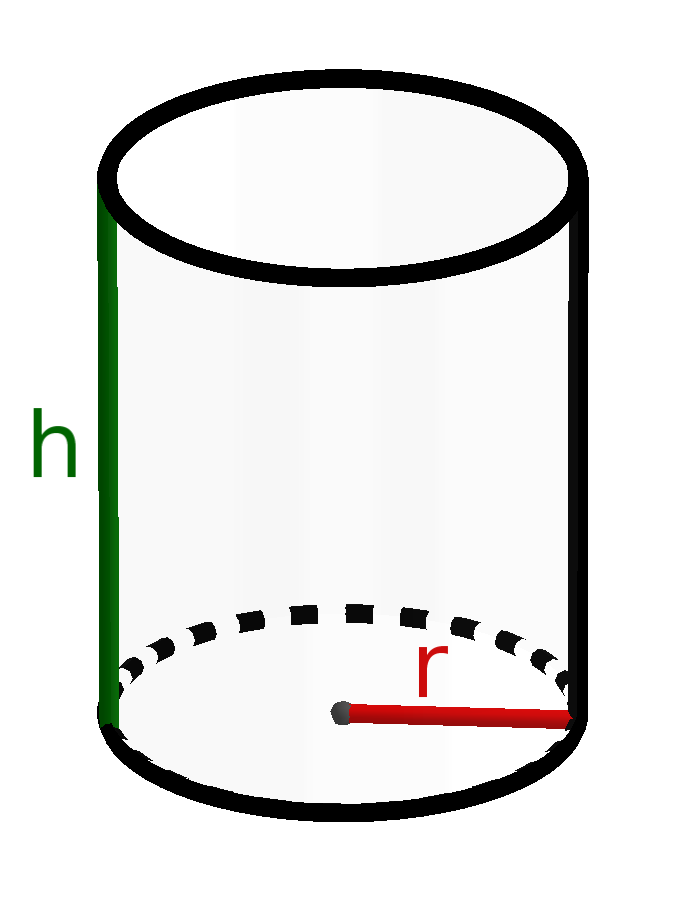
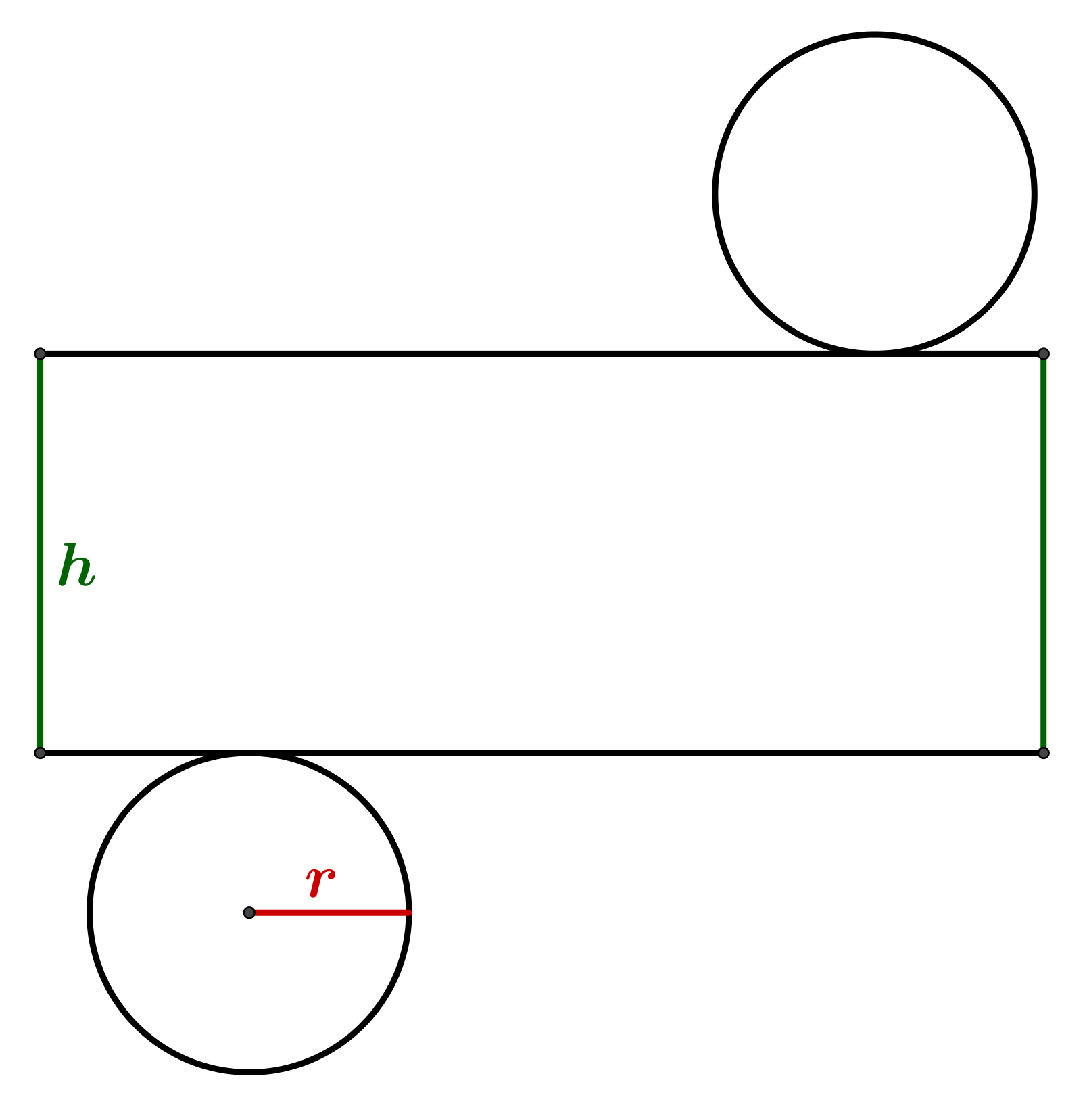
Netz des Zylinders:
Kugel

Es gibt kein Netz für eine Kugel.
Pyramide
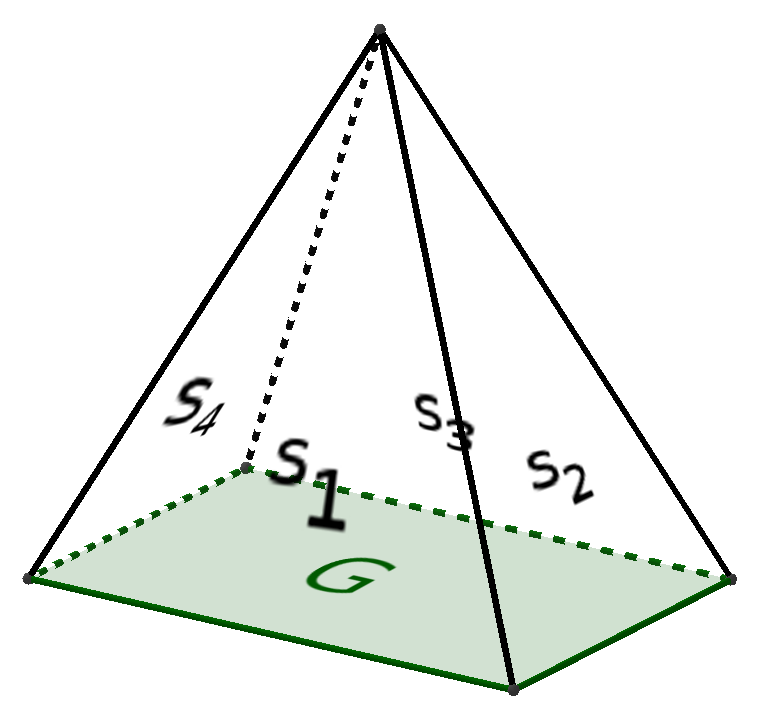
Netz der Pyramide:

Kegel
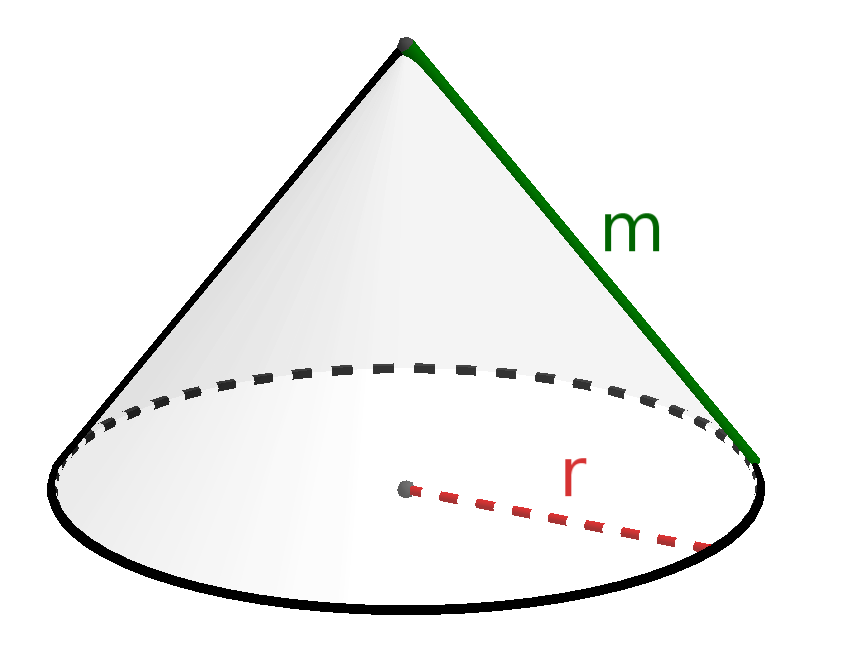
Netz des Kegels: