Volumenformeln

Von inyono 20.11.2018, 11:56:45

Titel

Inhalt 🟠

Bei vielen Körpern kann man das Volumen mit Formeln berechnen. Hier ist eine Übersicht über die wichtigsten Formeln.

Standardkörper

$V = l \cdot b \cdot h$

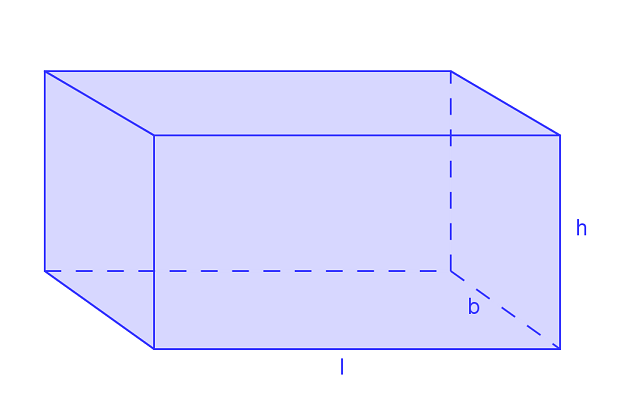
Alt: QuaderLink: (kein Link)

Zum Artikel Quader

$V = G \cdot h$

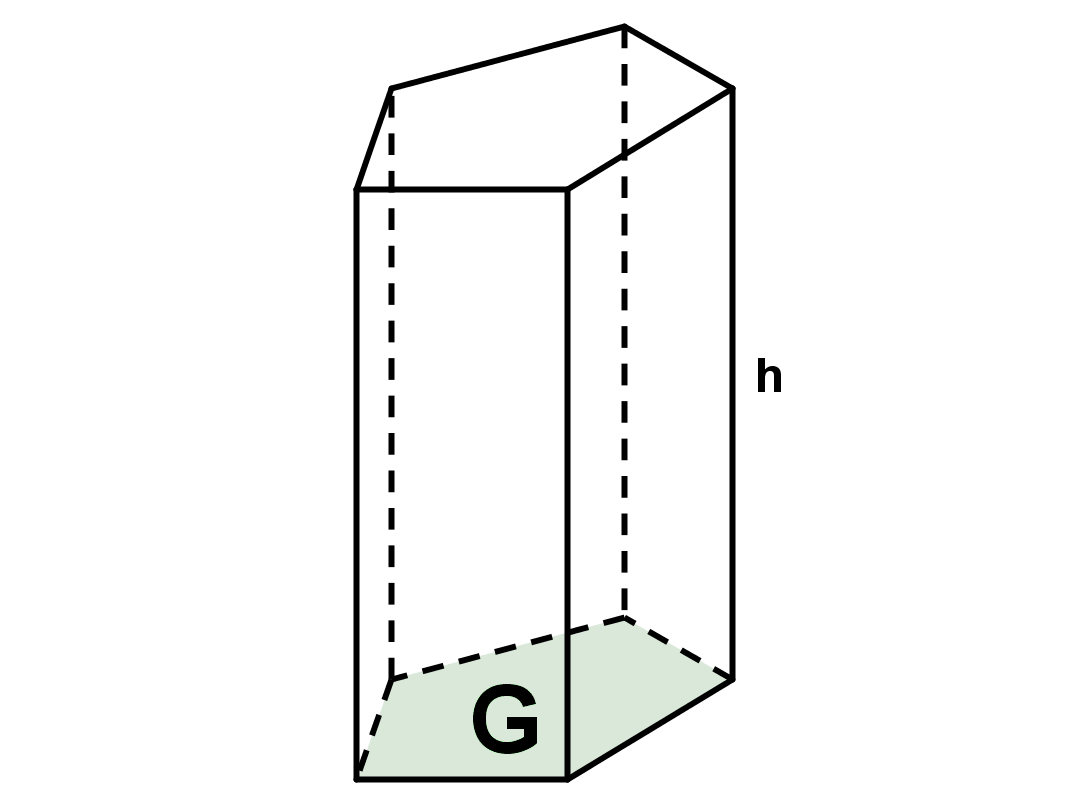
Alt: Bild eines PrismasLink: (kein Link)

Zum Artikel Prisma

$V = G \cdot h = r^{2} \cdot π \cdot h$

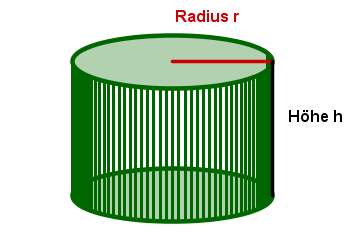
Alt: Rotation von einem RechteckLink: (kein Link)

Zum Artikel Zylinder

$V = \frac{4}{3} \cdot r^{3} \cdot π$

Alt: Rotation von einem KreisLink: (kein Link)

Zum Artikel Kugel

$V = \frac{1}{3} \cdot G \cdot h$

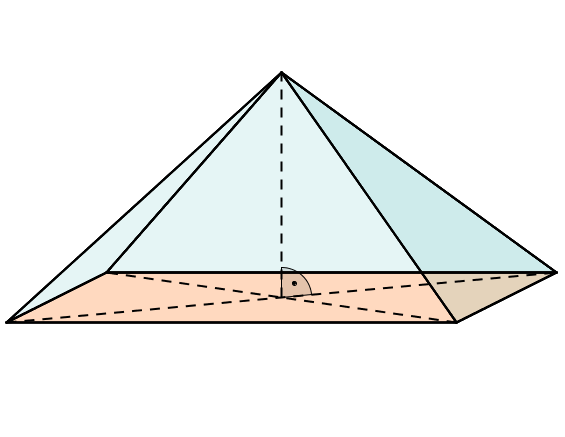
Alt: Geogebra File: https://assets.serlo.org/legacy/9980_jvY2SeSE2r.xmlLink: (kein Link)

Zum Artikel Pyramide

$\begin{array}{l} V = \frac{1}{3} \cdot G \cdot h \\ = \frac{1}{3} \cdot r^{2} \cdot π \cdot h \end{array}$

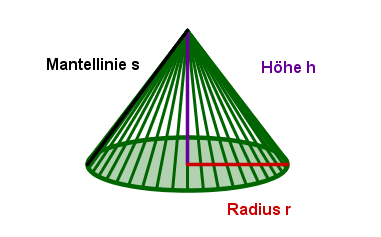
Alt: Rotation von einem rechtwinkligen DreieckLink: (kein Link)

Zum Artikel Kegel

$V = a \cdot a \cdot a = a^{3}$

Alt: WürfelLink: (kein Link)

Zum Artikel Würfel

$V = \frac{a^{3}}{12} \cdot \sqrt{2}$

Alt: TetraederLink: (kein Link)

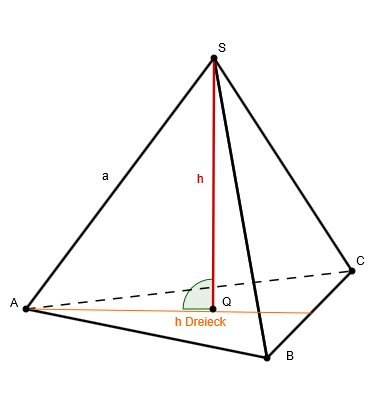
Zum Artikel Tetraeder

Applet

url:

Meta-Beschreibung

In diesem Artikel lernst du, wie du das Volumen von einigen Körpern berechnest. Ebenso zeigen wir dir die Ausnahmefälle auf.