Ein Kegel ist
ein dreidimensionaler Körper,
der entsteht, wenn man
alle Punkte eines Kreises
mit einem Punkt außerhalb der Kreisebene
verbindet.
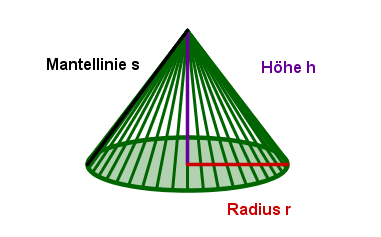
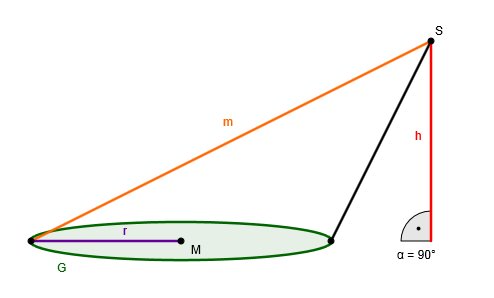
Skizze eines Kegels
Begriff Kegel
Der richtige Ausdruck für diesen Körper ist eigentlich Kreiskegel. In der höheren Mathematik werden nämlich manchmal auch Kegel betrachtet, deren Grundfläche kein Kreis ist.
In der Schule geht es in der Regel um gerade Kreiskegel. Bei geraden Kreiskegeln liegt die Spitze des Kegels senkrecht über dem Mittelpunkt der Grundfläche.
Bemerkung:
Ein gerader Kreiskegel entsteht, wenn sich ein rechtwinkliges Dreieck um eine seiner Katheten dreht.
Der entstehende Rotationskörper ist ein gerader Kreiskegel, dessen Höhe die Länge der Kathete ist, um die rotiert wurde. Der Grundkreisradius ist die Länge der anderen Kathete.
Beispiele für Kegel in der realen Welt
Manche Alltagsgegenstände haben annähernd die Gestalt eines Kegels. Hier ein paar Beispiele:

Ein kegelförmiger Partyhut

Auch dieser Markierungshut hat, wenn man ihn sich "richtig" spitz denkt, ungefähr Kegelform.

Die Eistüte hat die Form eines Kegels, und in diesem Fall annähernd sogar auch das Eis.
Volumen eines Kegels
: Grundfläche des Kegels
: Höhe des Kegels
: Radius der Grundfläche
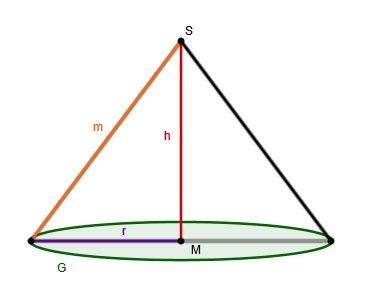
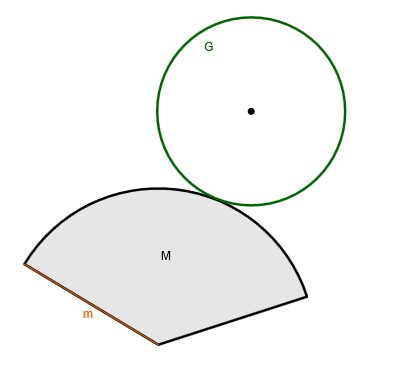
Oberflächeninhalt eines Kegels
Schiefer Kegel
Die Spitze eines Kegels muss nicht senkrecht über dem Mittelpunkt der Grundfläche liegen. Liegt er nicht genau darüber, spricht man von einem schiefen Kegel.
Das Volumen verändert sich bei gleicher Höhe nicht, der Oberflächeninhalt jedoch schon.
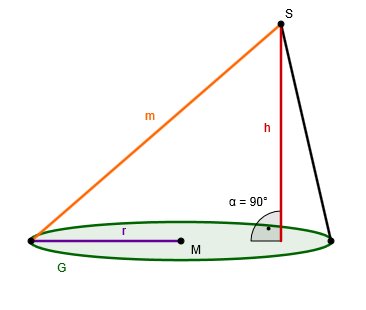
Übungsaufgaben
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zum Kegel
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
