Aufgaben zum Kegel

Hier findest du Übungsaufgaben rund um den Kegel. Bearbeite Sach- und Rechenaufgaben, finde Kegelnetze, berechne Volumen, Oberflächeninhalte und vieles mehr.

1
Der Kegel: Ziehe die Wörter in die passenden Lücken.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kegel
1. Ein Kegel ist ein dreidimensionaler Körper.
2. Er entsteht, wenn man alle Punkte eines Kreises mit einem Punkt außerhalb der Kreisebene verbindet.
3. Der richtige Ausdruck für diesen Körper ist eigentlich Kreiskegel.
4. Beim geraden Kreiskegel liegt die Spitze des Kegels senkrecht über dem Mittelpunkt der Grundfläche.
5. Manche Alltagsgegenstände haben die Form eines Kegels, z.B. eine Eiswaffel oder ein Markierungshütchen.
2
Das Glas ist (ohne Stiel) 7 cm hoch und hat oben den Umfang 26,7 cm.
Wie groß ist das Volumen des Glases?
cm³
Für diese Aufgabe benötigst Du folgendes Grundwissen: Kegel
Berechnung des Grundkreisradius r
Um das Volumen des kegelförmigen Glases zu berechnen, musst du zuerst den Grundkreisradius r berechnen, indem du die Formel für die Berechnung des Umfangs eines Kreises nach r umformst. Du musst dazu auf beiden Seiten der Gleichung durch 2π teilen.
$\begin{array}{rcll} U & = & 2 \cdot π \cdot r & | : (2 \cdot π) \\ r & = & \frac{U}{2 \cdot π} \end{array}$
Jetzt kannst du U in die Gleichung einsetzen.
$r = \frac{26,7 cm}{2 \cdot π} \approx 4,25 cm$
Berechnung des Volumens V von dem kegelförmigen Glas
Du kannst nun den Radius und die Höhe in die Formel zur Berechnung des Volumens eines Kegels einsetzen.
$\begin{array}{rcl} V & = & \frac{1}{3} \cdot π \cdot r^{2} \cdot h \\ = & \frac{1}{3} \cdot π \cdot (4,25 cm)^{2} \cdot 7 c m \\ = & \frac{1}{3} \cdot π \cdot 18.0625 {cm}^{2} \cdot 7 cm \\ \approx & 132,41 {cm}^{3} \end{array}$
Antwort:
Das Volumen V des kegelförmigen Glases beträgt ca. $132 {cm}^{3}$ .
Gegeben:
Höhe des Kegelglases h=7 cm
Umfang des Grundkreises U=26,7 cm
Gesucht:
Volumen des Kegelglases V
Um das Volumen zu berechnen, kannst du folgendermaßen vorgehen:
Berechne zuerst den Grundkreisradius des Kegels.
Berechne damit das Volumen
3
Betrachte den geraden Kegel. Der Radius der Grundfläche ist $r = 3$ und der Winkel $φ$ ist $60 °$ .
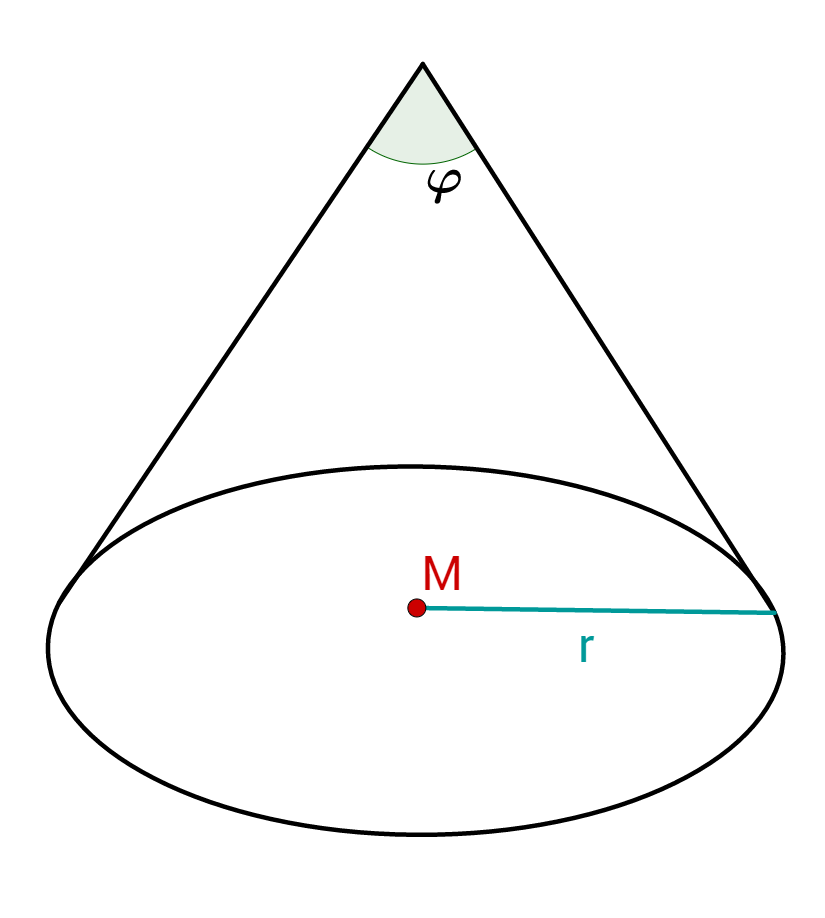
1. Berechne das Volumen des Kegels.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Kegel
  Die gesuchte Formel lautet:
  $V = \frac{1}{3} \cdot G \cdot h = \frac{1}{3} π r^{2} \cdot h$
  Überleg dir nun, welche der Variablen in der Aufgabe gegeben sind und welche du noch suchst.
  gegeben:
  $r = 3$
  $φ = 60 °$
  gesucht:
  $V$ , $h$
  Das Volumen V kannst du erst ausrechnen, wenn du die Höhe h gefunden hast.
  Berechnen der Höhe h
  Die Höhe des Kegels erhältst du durch einen Querschnitt durch den Mittelpunkt $M$ und die Spitze $S$ . Dieser sieht folgendermaßen aus:
  Dieses Dreieck kannst du nun halbieren, so dass du ein rechtwinkliges Dreieck erhältst.
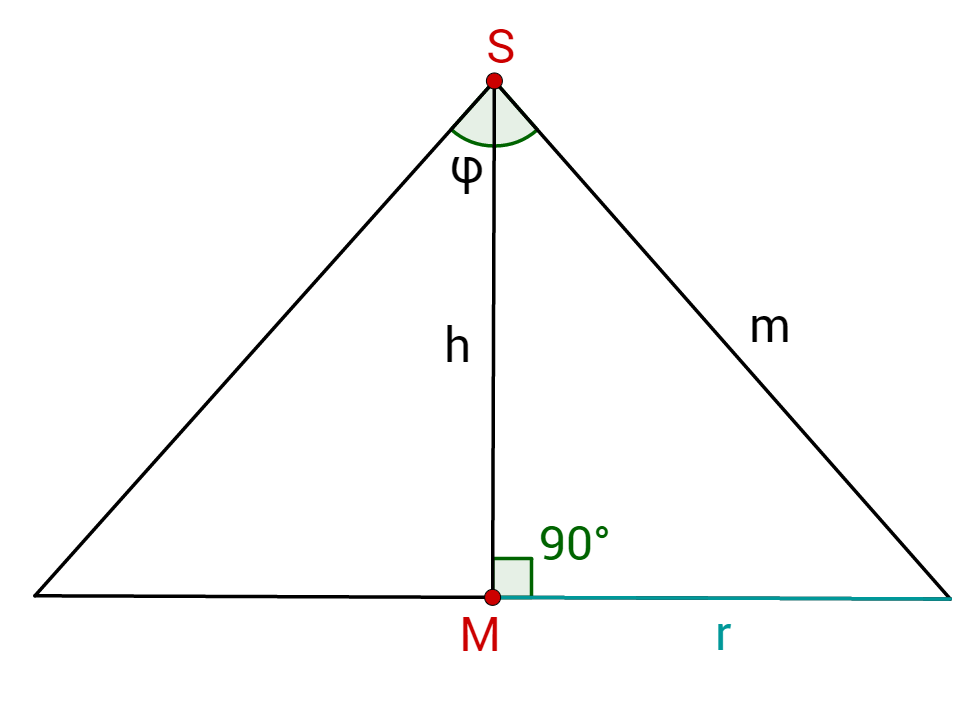
  In diesem Dreieck kennst du die Strecke $r$ (Gegenkathete von $\frac{φ}{2}$ ).
  Die gesuchte Größe ist die Höhe $h$ . Diese ist die Ankathete von $\frac{φ}{2}$ .
  Du kannst $h$ mithilfe einer trigonomischen Funktion (Sinus, Kosinus oder Tangens) ausrechnen.
  $t a n (\frac{φ}{2}) = \frac{G e g e n k a t h e t e}{A n k a t h e t e} = \frac{r}{h}$
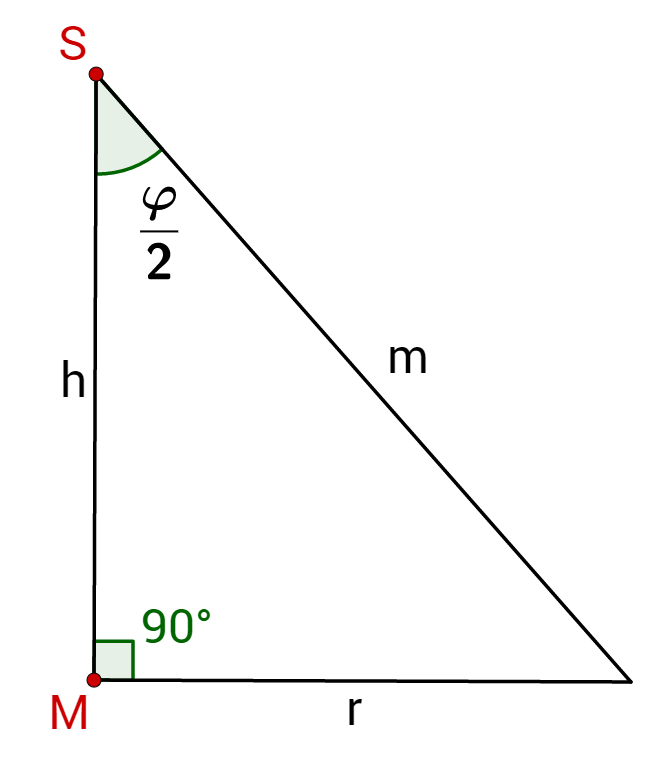
  Du kannst den Tangens von $\frac{φ}{2}$ benutzen um auf $h$ zu kommen. Anschließend musst du die Formel nach $h$ umstellen.
  $\begin{array}{rcll} \tan (\frac{φ}{2}) & = & \frac{r}{h} & | \cdot h \\ \tan (\frac{φ}{2}) \cdot h & = & r & | : \tan (\frac{φ}{2}) \\ h & = & \frac{r}{t a n (\frac{φ}{2})} \end{array}$
  (Beachte: Diese Umformungen sind nur gültig, wenn $t a n (\frac{φ}{2}) ≠ 0$ ist. Das ist in unserem Fall mit $φ = 60 °$ der Fall.)
  Setze die Werte ein und berechne die Höhe des Kegels!
  $h = \frac{r}{t a n (\frac{φ}{2})} = \frac{3}{t a n (\frac{60 °}{2})} = \frac{3}{\frac{1}{\sqrt{3}}} = 3 \sqrt{3} \approx 5,20$
  
  Die Höhe des Kegels beträgt $3 \sqrt{3} \approx 5,20$ .
  Berechnung des Volumens
  Das Volumen können wir nun mit der bekannten Formel berechnen. Setze dazu die bekannten Werte in die Formel ein und berechne das Volumen!
  $V = \frac{1}{3} \cdot G \cdot h = \frac{1}{3} \cdot π r^{2} \cdot h$
  $V = \frac{1}{3} \cdot π \cdot (3)^{2} \cdot 3 \sqrt{3} \approx 49,0$
  Das Volumen des Kegels beträgt ca. $49,0$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Schau dir den Artikel zum Kegel an und suche die passende Formel für das Volumen heraus.
2. Berechne den Oberflächeninhalt des Kegels.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Kegel
  $O = M + G = r \cdot m \cdot π + r^{2} π$
  In der Formel haben wir alle Werte gegeben außer die Mantellinie $m$ .
  Berechnung der Mantellinie
  Die Mantellinie $m$ erhältst du ähnlich wie die Höhe in der Teilaufgabe $a)$ über das rechtwinklige Dreieck.
  Benutze wieder eine trigonometrische Funktion, um die Mantellinie $m$ zu berechnen!
  $s i n (\frac{φ}{2}) = \frac{G e g e n k a t h e t e}{H y p o t e n u s e} = \frac{r}{m}$
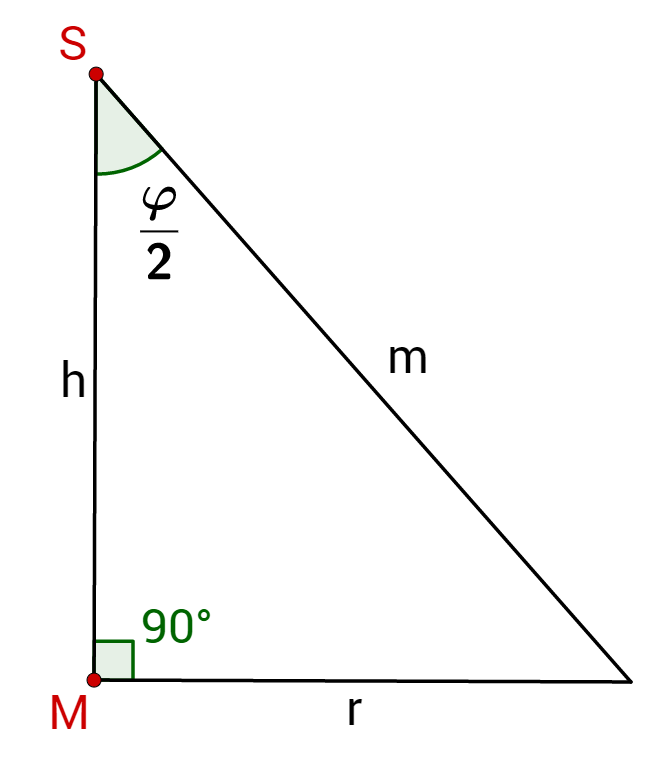
  Nutze den Sinus um $m$ mithilfe von $\frac{φ}{r}$ und $r$ zu berechnen. Und stelle die Gleichung entsprechend um!
  $s i n (\frac{φ}{2}) = \frac{r}{m} | \cdot m$
  $m \cdot s i n (\frac{φ}{2}) = r | : s i n (\frac{φ}{2})$
  $m = \frac{r}{s i n (\frac{φ}{2})}$
  Setze die Werte für $r$ und $φ$ ein und berechne die Mantellinie $m$ .
  $m = \frac{r}{s i n (\frac{φ}{2})} = \frac{3}{s i n (\frac{60 °}{2})}$
  $m = \frac{3}{s i n (30 °)} = \frac{3}{\frac{1}{2}} = 2 \cdot 3 = 6$
  Die Mantelfläche $m$ ist $6$ lang.
  Berechnung des Oberflächeninhalts
  Nutze die Formel für den Oberflächeninhalt des Kegels und setze die Werte ein.
  $O = M + G = r \cdot m \cdot π + r^{2} π$
  $O = 3 \cdot 6 \cdot π + (3)^{2} \cdot π = 27 π \approx 84,8$
  Die Oberfläche des Kegels beträgt ca. $84,8$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Den Oberflächeninhalt des Kegels erhältst du mithilfe einer Formel, die du im Artikel zum Kegel findest.
3. Zeichne ein sauberes Bild des Netzes von diesem Kegel.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Kegel
  Vorüberlegungen
  Beginne mit einer Skizze, in die du alle wichtigen Werte einzeichnest, die du kennen musst bevor du starten kannst.
  Skizze:
  In der nebenstehenden Skizze kennst du die Werte für $r$ und $m$ , dir fehlt aber der Wert für $α$ .
  Die Mantelfläche um $α$ ist ein Kreissektor. Schau dir dazu nochmals die Formeln an und versuche den Wert für den Mittelpunktswinkel $α$ zu berechnen.
  Der Mittelpunktswinkel berechnet sich folgendermaßen in einem Kreissektor:
  $\frac{α}{360 °} = \frac{A_{S e k t o r}}{A_{K r e i s}}$
  Mit $A_{K r e i s}$ ist die Fläche gemeint, die ein Kreis mit dem Radius $m$ hätte.
  Stelle jetzt die Flächen $A_{S e k t o r}$ und $A_{K r e i s}$ auf und setze sie in die Formel ein.
  Tipp: $A_{S e k t o r}$ entspricht der Mantelfläche des Kegels.
  $A_{S e k t o r} = M = r \cdot m \cdot π$
  $A_{K r e i s} = m^{2} \cdot π$
  $\frac{α}{360 °} = \frac{A_{S e k t o r}}{A_{K r e i s}}$
  $\frac{α}{360 °} = \frac{r \cdot m \cdot π}{m^{2} \cdot π}$
  Kürzen ergibt:
  $\frac{α}{360 °} = \frac{r}{m}$
  Stelle die Gleichung nach $α$ um!Und setze die Werte ein.
  $\frac{α}{360 °} = \frac{r}{m} | \cdot 360 °$
  $α = \frac{r}{m} \cdot 360 ° = \frac{3}{6} \cdot 360 ° = \frac{1}{2} \cdot 360 °$
  $α = 180 °$
  Dieser Kegel hat einen Mittelpunktswinkel seiner Mantelfläche von $180 °$ .
  Konstruktion des Kegel - Netzes
  Beginne mit der Mantelfläche und zeichne dazu den Mittelpunktswinkel $α$ an den Punkt der Spitze $S$ .
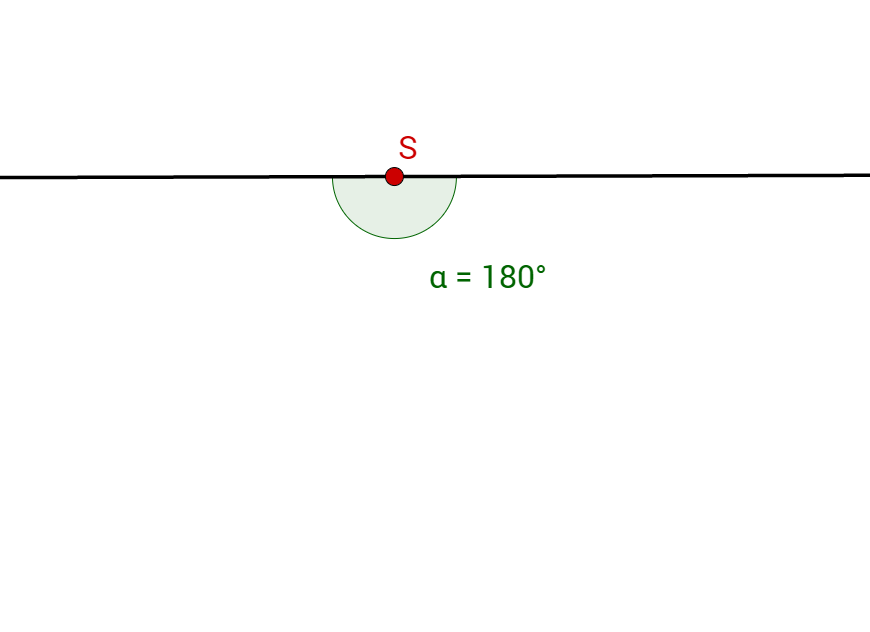
  Zeichne einen Halbkreis mit dem Radius $m = 6 c m$ um den Punkt $S$ .
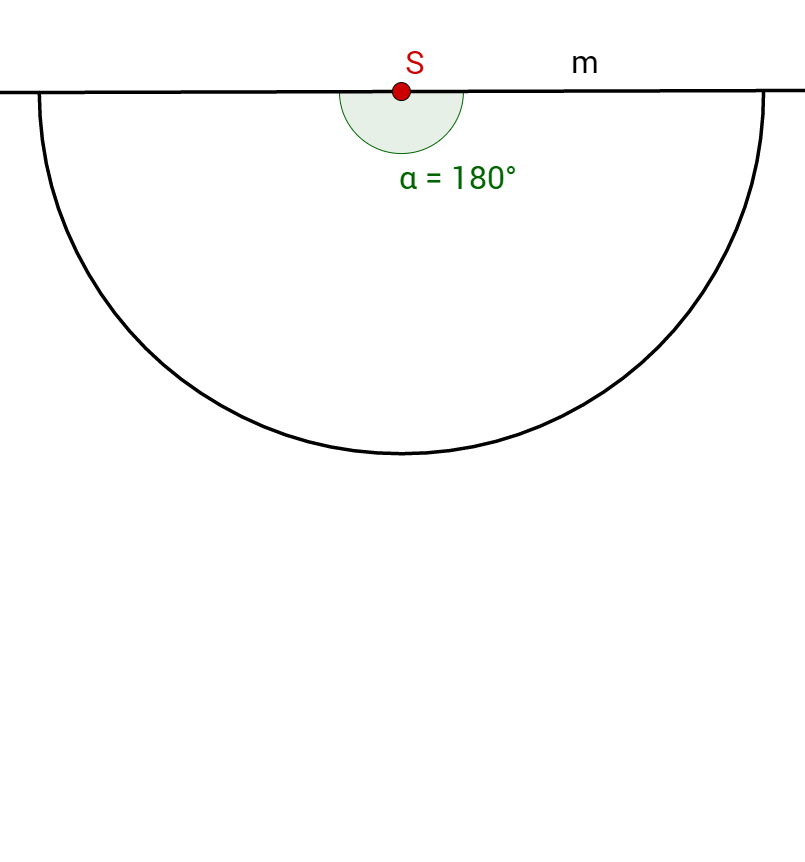
  Suche dir einen beliebigen Punkt am Halbkreis, an dem die Grundfläche $G$ des Kegels die Mantelfläche berührt. Benenne ihn! Zum Beispiel mit $A$ .
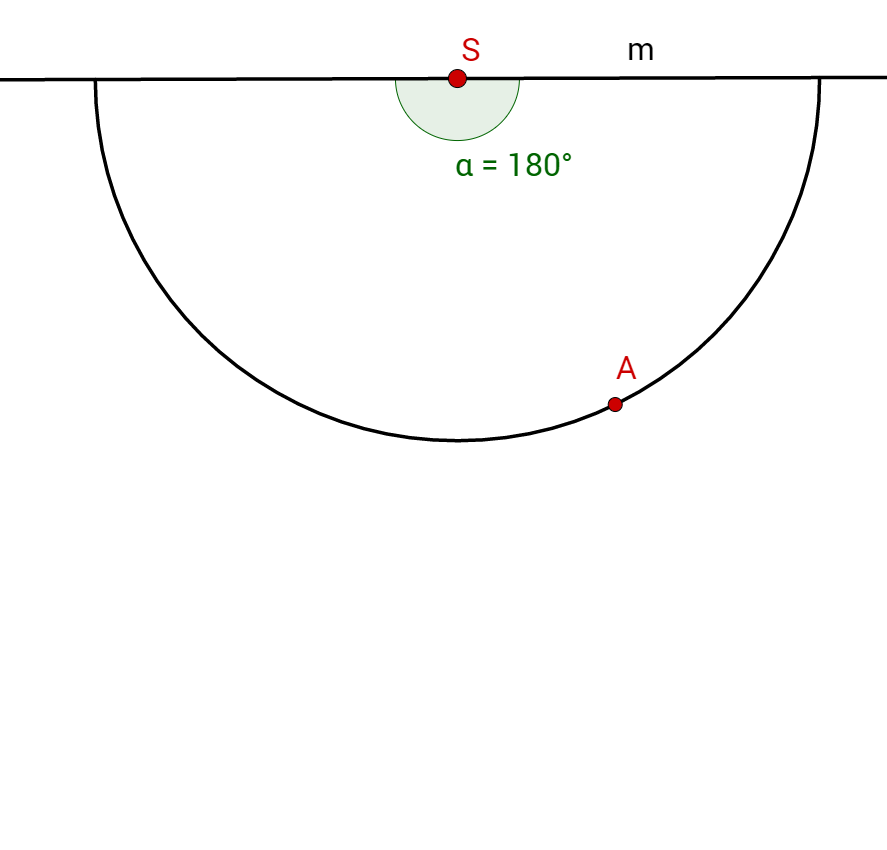
  Verbinde den Punkt $S$ mit dem Punkt $A$ durch eine Halbgerade!
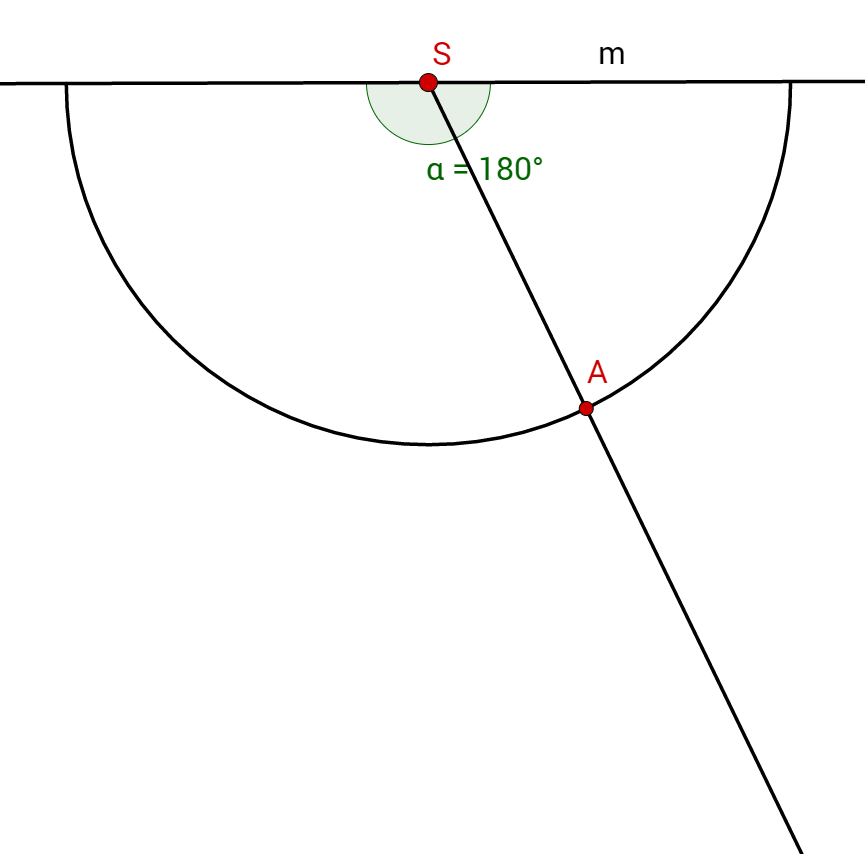
  Am Punkt $A$ trägst du nun den Radius $r = 3 c m$ ab und erhältst einen Schnittpunkt mit der Halbgerade.
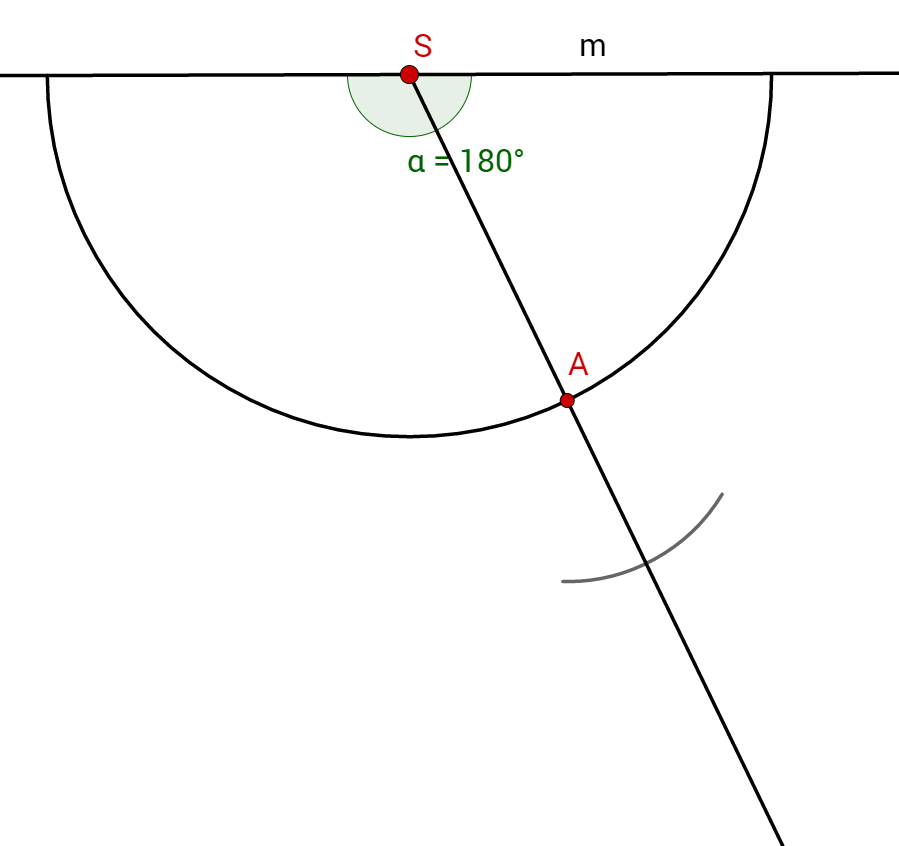
  Dieser Schnittpunkt ist $M$ (Mittelpunkt der Grundfläche).
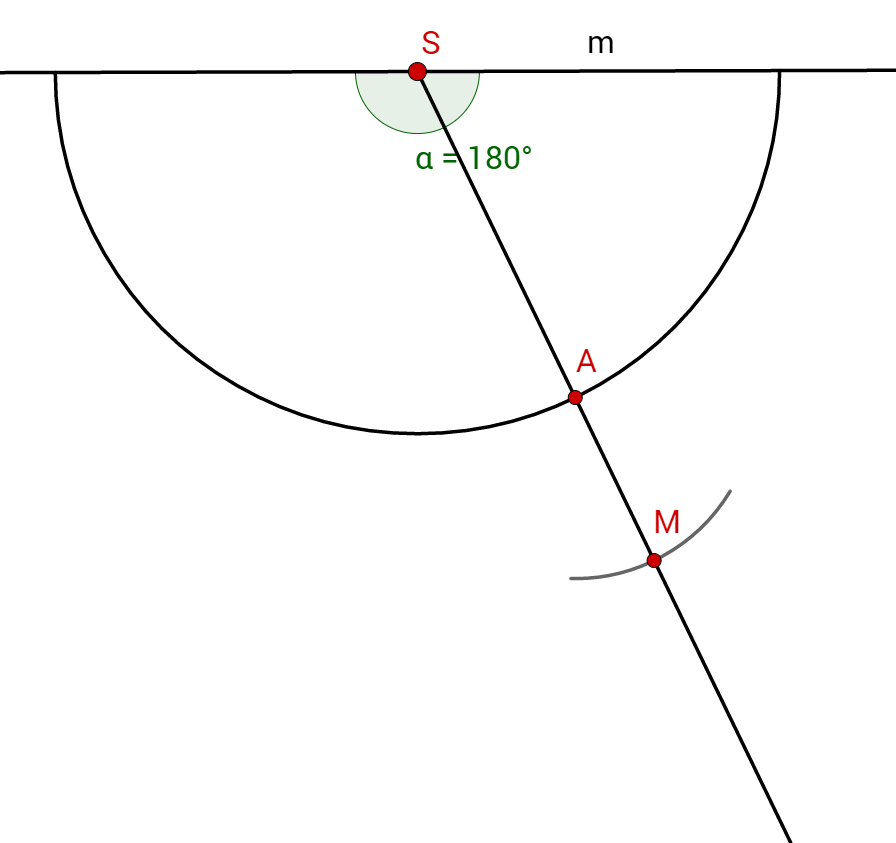
  Wenn du um $M$ den Kreis mit $r = 3 c m$ zeichnest hast du die Grundfläche.
  Die türkis eingefärbte Fläche ist das Netz des Kegels.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Tipp: Im Artikel zum Kegel ist ein Bild des Netzes vom Kegel zu sehen. Überlege dir, wie es für deinen Kegel aussehen muss!
  Benutze für die $3$ aus der Angabe $3 c m$ in deinem Heft.
4
Berechne das Volumen eines Kegelstumpfs mit Höhe $h = 2 c m$ , Grundflächenradius $r_{2} = 3 c m$ und Deckelradius $r_{1} = 5 c m$ .

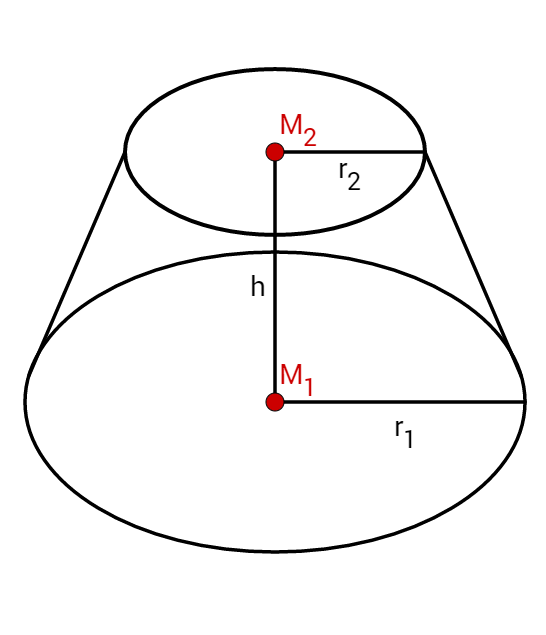
Für diese Aufgabe benötigst Du folgendes Grundwissen: Volumen eines Kegels
Volumen eines Kegelstumpfes berechnen
Um das Volumen eines solchen Kegelstumpfes zu berechnen, musst du dir vorstellen, dass der Kegel nicht "abgeschnitten" ist, sondern noch seine charakteristische Spitze hat. Dann kann man das gesamte Volumen dieses Kegels berechnen und die Spitze wieder abziehen. Zeichne dazu zuerst eine Skizze des gesamten Kegels!
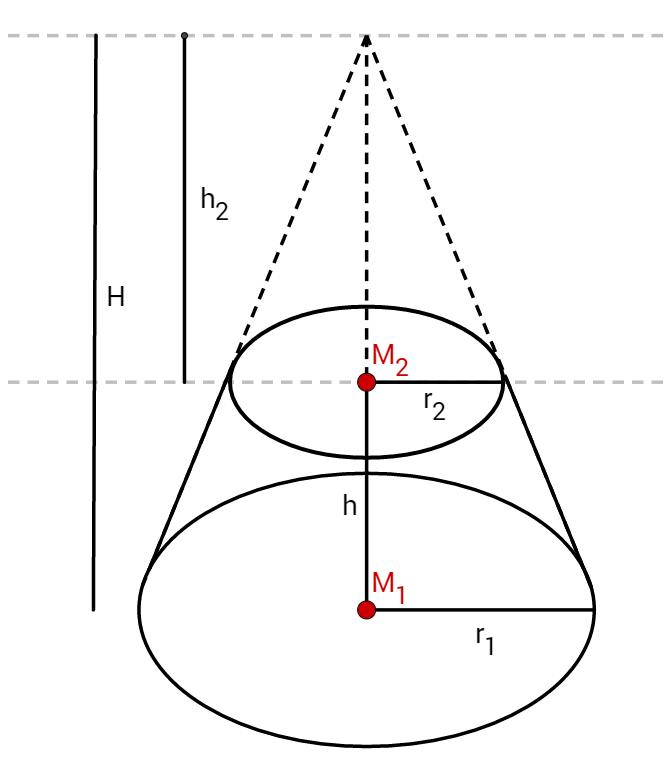
Deine Skizze sollte ungefähr so aussehen. Wichtig sind die Höhen.
$H = h + h_{2}$ ist die Höhe des gesamten Kegels, $h_{2}$ ist die Höhe der "imaginären" Spitze.
Jetzt musst du zuerst auf die Höhe $h_{2}$ kommen, dafür machst du am besten einen Querschnitt des Kegels.
Berechnung der Höhen $h_{2}$ und $H$
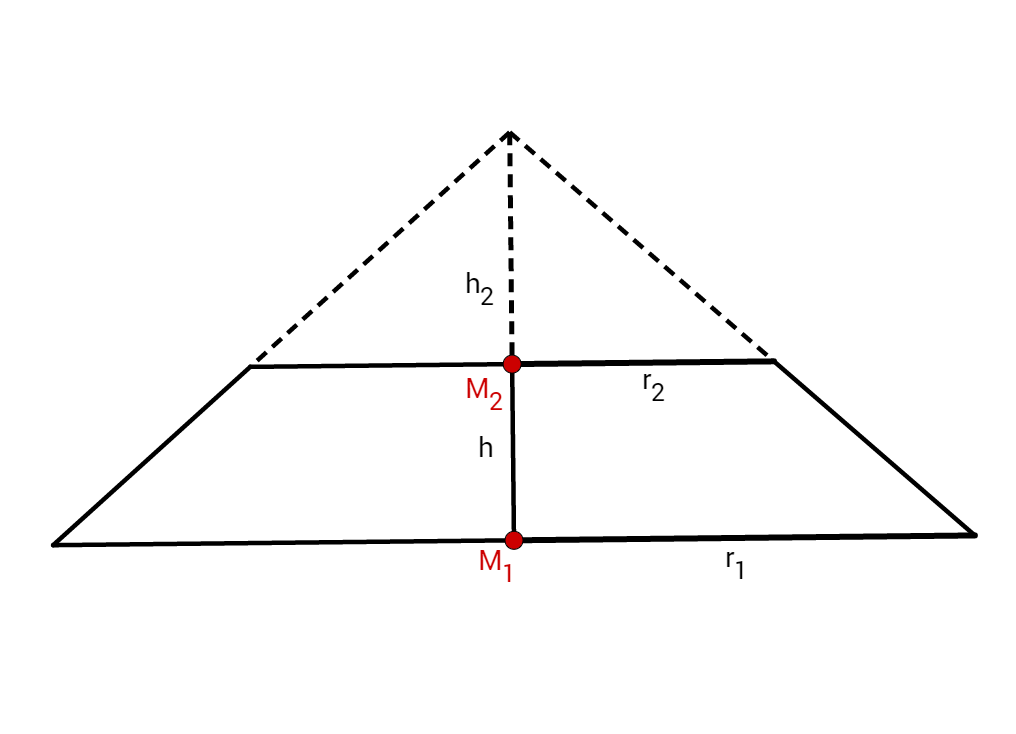
Bei dieser Skizze siehst du, dass es ausreichend ist, nur die rechte Seite des Dreiecks zu betrachten. Außerdem kannst du eine senkrechte Linie auf $r_{1}$ einzeichnen, die genau auf den Endpunkt von $r_{2}$ trifft.
Die rechte Seite deines Querschnitts sollte ungefähr so aussehen.
Du hast nun die Verbindungslinie von $r_{1}$ und $r_{2}$ eingezeichnet (gestrichelt) und erhältst dadurch einen Abschnitt $d$ von $r_{1}$ mit $d = r_{1} - r_{2}$ .
Außerdem kannst du zwei ähnliche Dreiecke erkennen. Einmal das Dreieck rechts unten mit $d$ , $h$ und $φ$ und dann noch das Dreieck oben mit $r_{2}$ , $h_{2}$ und $φ$ .
Versuche nun die bekannten Strecken einzuzeichnen und den Winkel $φ$ zu bestimmen!
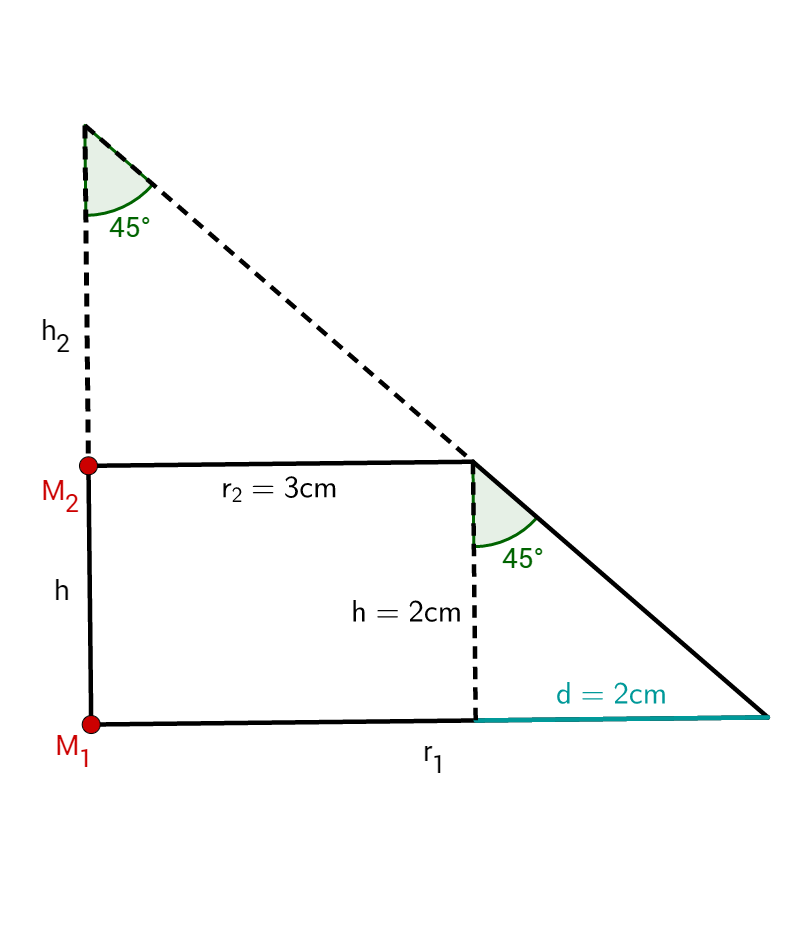
Das rechte untere Dreieck hat die Längen $h = 2 c m$ und
$d = r_{1} - r_{2} = 5 c m - 3 c m = 2 c m$ .
Damit hast du ein gleichschenkliges und rechtwinkliges Dreieck. Bei einem gleichschenkligen Dreieck hast du immer zwei gleiche Winkel und du hast zusätzlich noch einen $90 °$ Winkel.
Dadurch kommst du auf:
$180 ° = 90 ° + 2 \cdot φ$
Und erhältst: $φ = 45 °$ .
Durch eine Ähnlichkeitsbetrachtung kannst du nun auch $h_{2}$ berechnen.
Da du zwei ähnliche Dreiecke hast, muss das obere Dreieck auch gleichschenklig sein. Dadurch erhältst du:
$h_{2} = r_{2} = 3 c m$
Berechne nun die gesamte Höhe des Kegels $H$ und das Volumen $V_{g e s}$ des ganzen Kegels mit dem Radius $r_{1}$ und der Höhe $H$ .
Berechnung des gesuchten Volumens
$H = h + h_{2} = 2 c m + 3 c m = 5 c m$
$V_{g e s} = \frac{1}{3} \cdot r_{1}^{2} \cdot π \cdot H$
$V_{g e s} = \frac{1}{3} \cdot (5 c m)^{2} \cdot π \cdot 5 c m \approx 131 c m^{3}$
Von dem Gesamtvolumen $V_{g e s}$ ziehst du nun das Volumen des "imaginären" Kegels $V_{s p i t z e}$ mit der Höhe $h_{2}$ und dem Radius $r_{2}$ ab und erhältst so das Volumen des Kegelstumpfs $V_{s t u m p f}$ .
$V_{s t u m p f} = V_{g e s} - V_{s p i t z e}$
$V_{s p i t z e} = \frac{1}{3} \cdot r_{2}^{2} \cdot π \cdot h_{2}$
$V_{s p i t z e} = \frac{1}{3} \cdot (3 c m)^{2} \cdot π \cdot 3 c m \approx 28,3 c m^{3}$
$V_{s t u m p f} = 131 c m^{3} - 28,3 c m^{3} \approx 102,7 c m^{3}$
Das Volumen des Kegelstumpfs beträgt $V_{s t u m p f} \approx 102,7 c m^{3}$ .
Ergänze den Kegelstumpf, so dass ein vollständiger Kegel entsteht dessen Volumen du berechnen kannst. Ziehe anschließend das Volumen der "imaginären" Kegelspitze wieder ab!
5
An einem Stück gehärtetem Stahl mit $d = 12$ mm und $l = 120$ mm soll eine Körnerspitze geschliffen werden. Der Spitzwinkel $β$ soll 90 Grad betragen.
Das Stahlstück ist vor der Bearbeitung ein Zylinder.
Dann wird eine Spitze angeschliffen, so dass der Winkel an der Spitze $90^{\circ}$ ist.
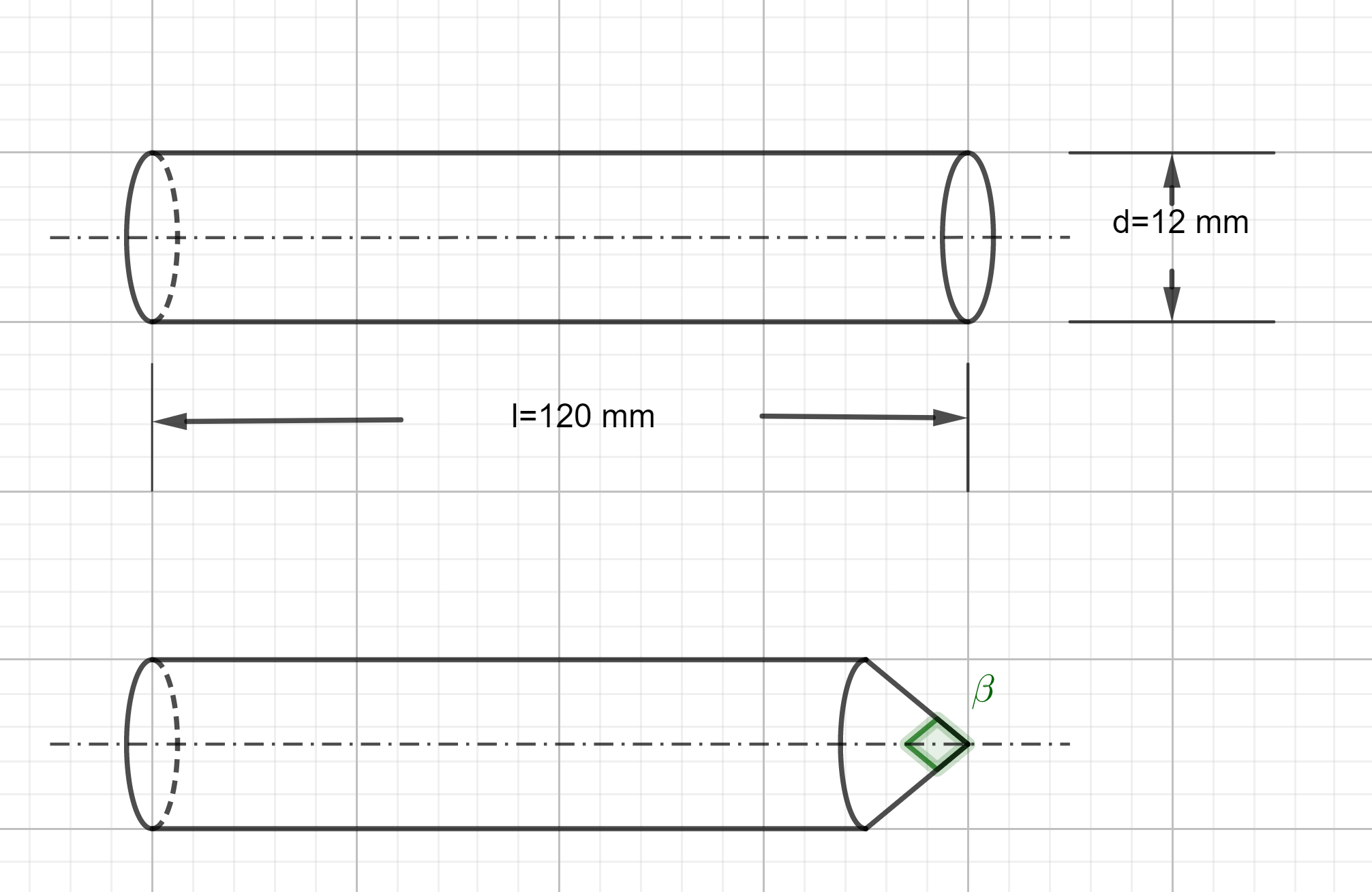
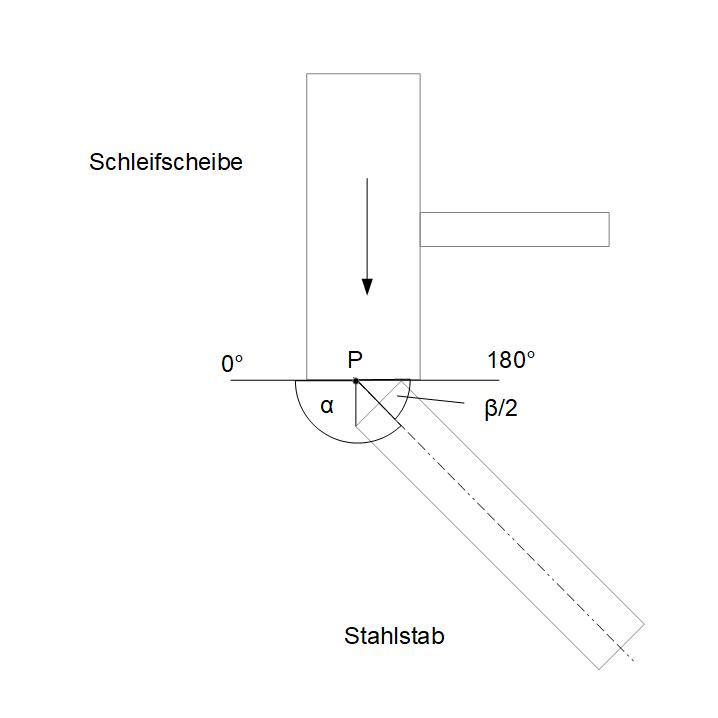
1. In welchem stumpfen Winkel $α$ muss der Stahl an die Schleifscheibe angelegt werden?
  
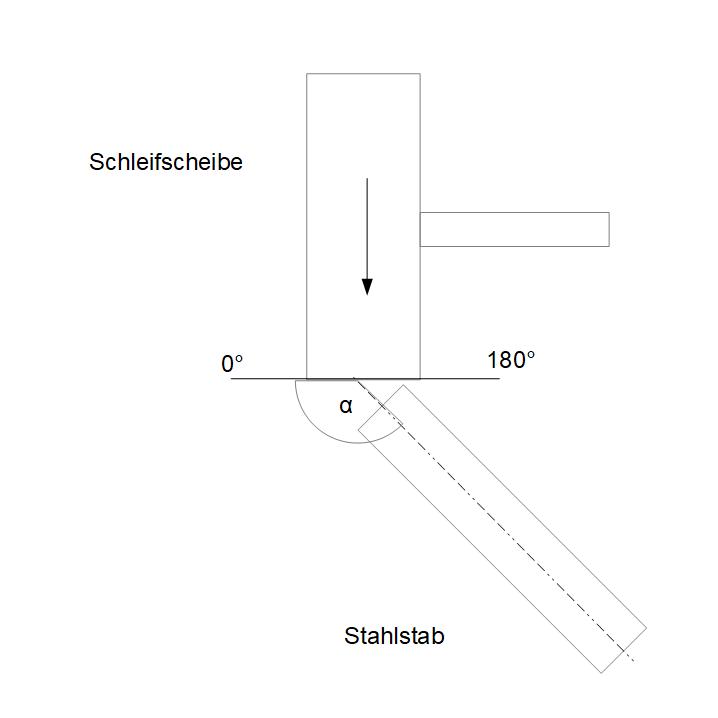
  Nun sieht man, dass die Körnerspitze in Punkt P mit der Stirnseite der Schleifscheibe einen gestreckten Winkel von 180° bildet. Subtrahiert man von diesem nun $\frac{β}{2}$ erhält man $α$
  $α$ $=$ $180^{\circ} - \frac{β}{2}$
  $=$ $180^{\circ} - \frac{90^{\circ}}{2}$
  $=$ $135^{\circ}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Fertige eine Skizze mit Schleifscheibe und Körnerspitze an. Eine Seite des Körnekegels muss dabei an der Stirnseite der Schleifscheibe anliegen.
2. Wie viel Stahl muss abgeschliffen werden? Angabe in ${mm}^{3}$ .
  
  Es genügt hier die Körnerspitze aufzuzeichnen mit Durchmesser, Radien, Höhe und halbem Spitzwinkel. Das Volumen des abzuschleifenden Stahls ist das Zylindervolumen mit d und h abzüglich des Kegelvolumens mit d und h.
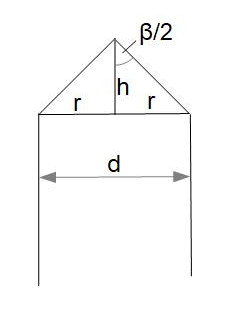
  Schritt 1: Bestimmung der Höhe $h$
  Der Winkel $\frac{β}{2} = 45 °$ liegt in einem rechtwinkligen Dreieck. Da jedes Dreieck eine Innenwinkelsumme von 180° hat und mit $90^{\circ}$ und $45^{\circ}$ zwei Winkel bekannt sind, muss auch der andere Winkel $45^{\circ}$ sein (denn es ist $180^{\circ} - 90^{\circ} - 45^{\circ} = 45^{\circ}$ ). Damit ist das Dreieck gleichschenklig. Die Höhe $h$ ist damit gleich $r$ und wir können sie damit folgendermaßen berechnen:
  $h = r = \frac{d}{2}$
  $h = \frac{12 m m}{2} = 6 mm$
  Schritt 2: Berechnung des abzuschleifenden Volumens
  $V$ $=$ $V_{Zylinder} - V_{Kegel}$
  $=$ $\frac{π \cdot d^{2} \cdot h}{4} - \frac{π \cdot d^{2} \cdot h}{12}$
  ↓
  Hauptnenner suchen und kürzen
  $=$ $\frac{π \cdot d^{2} \cdot h}{6}$
  ↓
  Werte einsetzen
  $=$ $\frac{π \cdot 12^{2} \cdot 6 {mm}^{3}}{6}$
  $=$ $452,39 {mm}^{3}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Um wie viel Gramm ist der Stab nach den Schleifen leichter?
  Hinweis: das spezifische Gewicht von Stahl beträgt $7,85 g / c m^{3}$
  
  Das abzuschleifende Volumen beträgt $452,39 m m^{3}$
  Zur Umwandlung in $c m^{3}$ das Volumen durch tausend teilen:
  $V = 0,45239 c m^{3}$
  Nun kann die Masse berechnet werden:
  $m = 7,85 \frac{g}{c m^{3}} \cdot 0,45239 c m^{3}$
  $= 3,55 g$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Die Masse eines Körpers berechnet sich aus dessen spezifischem Gewicht multipliziert mit dem Volumen:
  $m = ρ \cdot V$
4. Der Spitzwinkel soll nun um 10 Grad verringert werden. In welchen Winkeln kann der Stahl an der Schleifscheibe geschliffen werden?
  
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Neuer Spitzwinkel:
  $β_{2} = β - 10 °$
  $= 90 ° - 10 °$
  $= 80 °$
  Für den stumpfen Schleifwinkel gilt:
  $α = 180 ° - \frac{β_{2}}{2}$
  $= 180 ° - \frac{80 °}{2}$
  $= 140 °$
  Für einen spitzen Schleifwinkel gilt auch:
  $α = \frac{β_{2}}{2}$
  $= \frac{80 °}{2}$
  $= 40 °$
6
strobl-f.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Franz Strobl
Ein Kegel, dessen Höhe $h$ so groß ist wie der Grundkreis-Durchmesser, habe das Volumen $1 L i t e r$ .
1. Berechne $h$ .
  
  Lösung zur 1. Frage der Aufgabe:
  gegeben:
  Grundkreisdurchmesser des Kreiskegels $d=h$
  Volumen $V = 1 l$
  gesucht:
  Höhe des Kreiskegels $h$
  Darstellen des Grundkreisradius mit $h$
  Um die Höhe $h$ zu berechnen, kannst du zuerst den Radius $r$ als $h$ geteilt durch zwei darstellen, denn $d$ gleicht $h$ und ist außerdem doppelt so lang wie $r$ .
  $r= \frac{d}{2}$
  $r = \frac{h}{2}$
  Aufstellen eines Gleichungssystemes:
  $r = \frac{h}{2}$ ein Gleichungssystem mit zwei Gleichungen auf.
  Gleichung (I) ist die Darstellung von $r$ mit $h$ .
  Gleichung (II) ist die Formel für die Berechnung des Volumens von einem Kreiskegel mit den eingesetzten Wert von $r= \frac{h}{2}$
  (I): $r= \frac{h}{2}$
  (II): $\frac{1}{3} \cdot r^{2} \cdot π \cdot h = 1 l$
  Nun löst du das Gleichungssystem mit dem Einsetzungsverfahren, wobei du die Gleichung (I) ind (II) einsetzst.
  (I) in (II):
  $\frac{1}{3} \cdot \frac{h^{2}}{2^{2}} \cdot π \cdot h = 1 l$
  $\frac{1 \cdot h^{2} \cdot h \cdot π}{3 \cdot 4}$ $=$ $1 l$
  $\frac{1 \cdot h^{2} \cdot h \cdot π}{3 \cdot 4}$ $=$ $1 l$ $\cdot 12$
  $h^{3} \cdot π$ $=$ $12 \cdot 1 l$
  $h^{3} \cdot π$ $=$ $12 l$ $: π$
  $h^{3}$ $=$ $\frac{12 l}{π}$ $\sqrt[3]{}$
  $h$ $=$ $\sqrt[3]{\frac{12 l}{π}}$
  $=$ $\sqrt[3]{\frac{12 {dm}^{3}}{π}}$
  $=$ $1,563185283593544 dm$
  $\approx$ $1,56 dm$
  Du kannst $r$ ausrechnen, indem du $h$ in Gleichung (I) einsetzst. Du benötigst den Radius $r$ , um die 2 Frage der Aufgabenstellung zu beantworten.
  $h$ in (I):
  $r = \frac{1,56 dm}{2} = 0,78 dm$
  Antwort zur 1. Frage der Aufgabe:
  Der Kreiskegel ist etwa $1,56 d m$ hoch.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Berechne nun den Mittelpunktswinkel $α$ des Sektors, aus dem dieser Kegel gefertigt werden kann
  
  Lösung zur 2. Frage der Aufgabe:
  Berechnung der Mantellinie s:
  Um den Mittelpunktswinkel α des Kreissektors, aus dem der Kegel gefertigt werden kann, zu bestimmen, musst du zuerst die Mantellinie $s$ des Kegels ausrechnen. Du musst dazu dir ein rechtwinkliges Dreieck vorstellen, welches den Grundkreismittelpunkt, irgendeinen Punkt auf der Kreislinie der Höhe und die Spitze des Kreiskegels verbindet. Der Grundkreismittelpunkt und der Punkt auf der Kreislinie verbinden sich zu einer Kathete und dem Grundkreisradius r. Der Punkt auf der Kreislinie verbindet sich mit der Kegelspitze zur Hypotenuse und der Mantellinie s. Die Kegelspitze verbindet sich mit dem Grundkreismittelpunkt zu der zweiten Kathete und der Höhe h. Da h und r bereits bekannt sind, kannst du s mit dem Satz des Pythagoras berechnen.
  $s^{2}$ $=$ $h^{2} + r^{2}$
  $=$ ${1,56}^{2} {dm}^{2} + {0,78}^{2} {dm}^{2}$
  $=$ $3,042 {dm}^{2}$ $\sqrt{}$
  $s$ $=$ $\sqrt{3,042 {dm}^{2}}$
  $\approx$ $1,74 dm$
  Anmerkung:
  Die Lösungen der Gleichung wären:
  $s_{1 / 2} = \pm \sqrt{3,042 {dm}^{2}}$
  Da s eine Länge ist, wäre eine negative Lösung nicht sinnvoll, weshalb du diese nicht weiter beachten musst.
  Berechnung des Mittelpunktswinkels $α$
  Nun kannst du $α$ berechnen, indem du dir bereits bekannte Werte in eine nach $α$ umgeformte Version von dieser Formel
  $\frac{α}{360^{\circ}} = \frac{2 \cdot π \cdot r}{2 \cdot π \cdot s} = \frac{r}{s}$
  einsetzst.
  $\frac{α}{360^{\circ}} = \frac{0,78 dm}{1,74 dm} | \cdot 360^{\circ}$
  Du multiplizierst auf beiden Seiten der Gleichung mit $360 °$ .
  $α = 0,45 \cdot 360^{\circ} = 162^{\circ}$
  Antwort:
  Der Mittelpunktswinkel α des Sektors, aus dem der Kegel gefertigt werden kann, ist $162 °$ groß.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$α$	$=$	$180^{\circ} - \frac{β}{2}$
	$=$	$180^{\circ} - \frac{90^{\circ}}{2}$
	$=$	$135^{\circ}$

$V$	$=$	$V_{Zylinder} - V_{Kegel}$
	$=$	$\frac{π \cdot d^{2} \cdot h}{4} - \frac{π \cdot d^{2} \cdot h}{12}$
	↓	Hauptnenner suchen und kürzen
	$=$	$\frac{π \cdot d^{2} \cdot h}{6}$
	↓	Werte einsetzen
	$=$	$\frac{π \cdot 12^{2} \cdot 6 {mm}^{3}}{6}$
	$=$	$452,39 {mm}^{3}$

$\frac{1 \cdot h^{2} \cdot h \cdot π}{3 \cdot 4}$	$=$	$1 l$
$\frac{1 \cdot h^{2} \cdot h \cdot π}{3 \cdot 4}$	$=$	$1 l$	$\cdot 12$
$h^{3} \cdot π$	$=$	$12 \cdot 1 l$
$h^{3} \cdot π$	$=$	$12 l$	$: π$
$h^{3}$	$=$	$\frac{12 l}{π}$	$\sqrt[3]{}$
$h$	$=$	$\sqrt[3]{\frac{12 l}{π}}$
	$=$	$\sqrt[3]{\frac{12 {dm}^{3}}{π}}$
	$=$	$1,563185283593544 dm$
	$\approx$	$1,56 dm$

$s^{2}$	$=$	$h^{2} + r^{2}$
	$=$	${1,56}^{2} {dm}^{2} + {0,78}^{2} {dm}^{2}$
	$=$	$3,042 {dm}^{2}$	$\sqrt{}$
$s$	$=$	$\sqrt{3,042 {dm}^{2}}$
	$\approx$	$1,74 dm$

Aufgaben zum Kegel

Berechnung des Grundkreisradius r

Berechnung des Volumens V von dem kegelförmigen Glas

Antwort:

Berechnen der Höhe h

Berechnung des Volumens

Hast du eine Frage oder Feedback?

Berechnung der Mantellinie

Berechnung des Oberflächeninhalts

Hast du eine Frage oder Feedback?

Vorüberlegungen

Konstruktion des Kegel - Netzes

Hast du eine Frage oder Feedback?

Volumen eines Kegelstumpfes berechnen

Berechnung der Höhen h2 und H

Berechnung des gesuchten Volumens

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Lösung zur 1. Frage der Aufgabe:

Antwort zur 1. Frage der Aufgabe:

Hast du eine Frage oder Feedback?

Lösung zur 2. Frage der Aufgabe:

Berechnung der Mantellinie s:

Anmerkung:

Berechnung des Mittelpunktswinkels α

Antwort:

Hast du eine Frage oder Feedback?

Berechnung der Höhen $h_{2}$ und $H$

Berechnung des Mittelpunktswinkels $α$