Betrachte den geraden Kegel. Der Radius der Grundfläche ist und der Winkel ist .
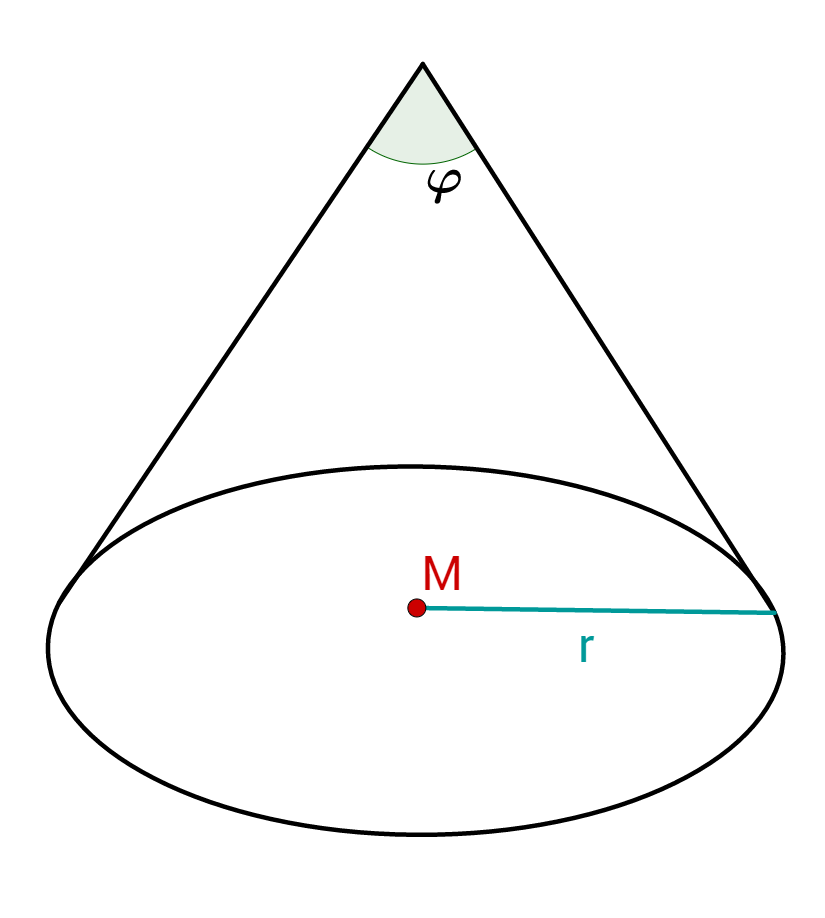
Berechne das Volumen des Kegels.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Kegel
Die gesuchte Formel lautet:
Überleg dir nun, welche der Variablen in der Aufgabe gegeben sind und welche du noch suchst.
gegeben:
gesucht:
,
Das Volumen V kannst du erst ausrechnen, wenn du die Höhe h gefunden hast.
Berechnen der Höhe h
Die Höhe des Kegels erhältst du durch einen Querschnitt durch den Mittelpunkt und die Spitze . Dieser sieht folgendermaßen aus:
Dieses Dreieck kannst du nun halbieren, so dass du ein rechtwinkliges Dreieck erhältst.
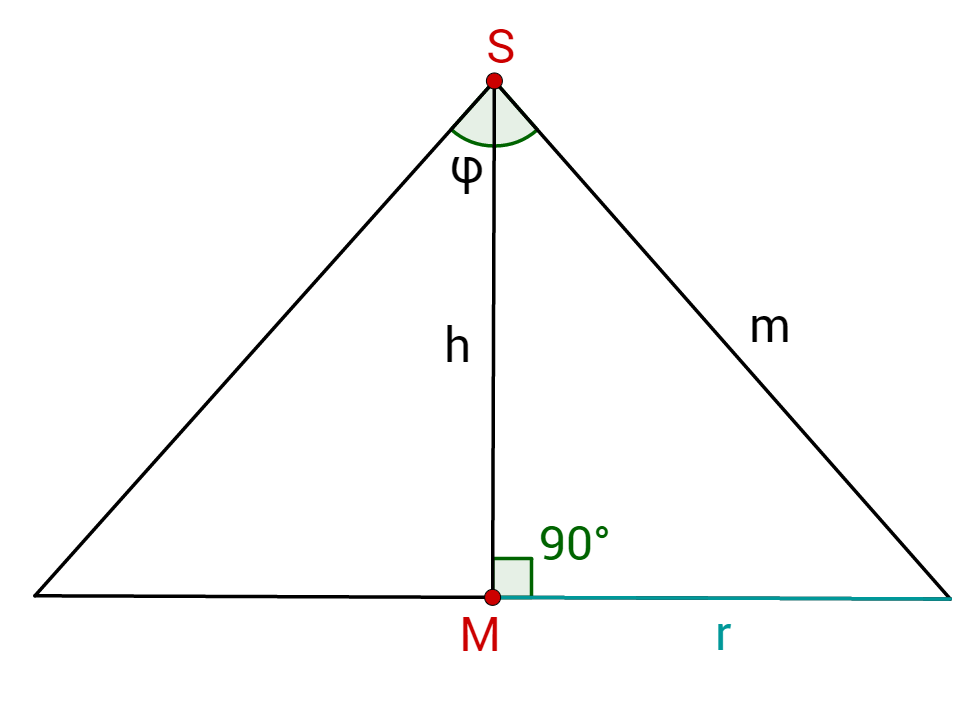
In diesem Dreieck kennst du die Strecke (Gegenkathete von ).
Die gesuchte Größe ist die Höhe . Diese ist die Ankathete von .
Du kannst mithilfe einer trigonomischen Funktion (Sinus, Kosinus oder Tangens) ausrechnen.
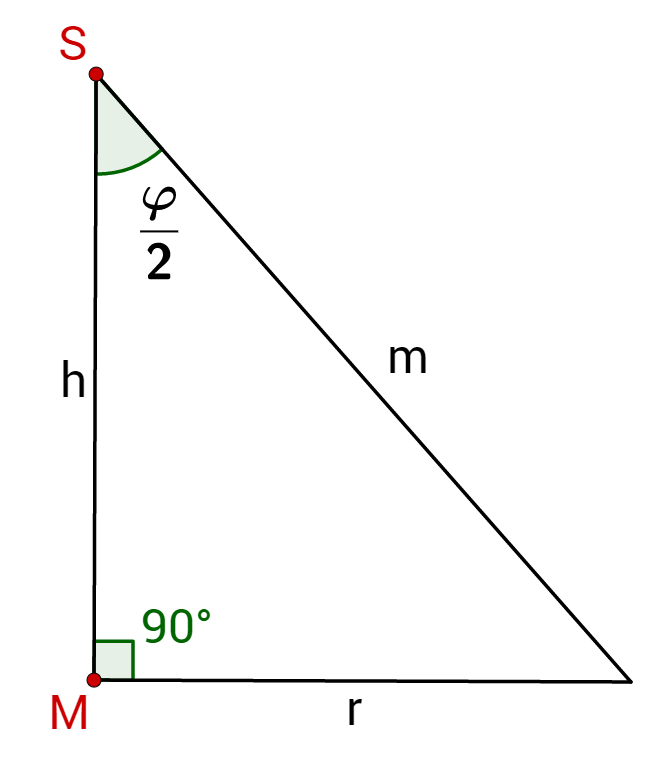
Du kannst den Tangens von benutzen um auf zu kommen. Anschließend musst du die Formel nach umstellen.
(Beachte: Diese Umformungen sind nur gültig, wenn ist. Das ist in unserem Fall mit der Fall.)
Setze die Werte ein und berechne die Höhe des Kegels!
Die Höhe des Kegels beträgt .
Berechnung des Volumens
Das Volumen können wir nun mit der bekannten Formel berechnen. Setze dazu die bekannten Werte in die Formel ein und berechne das Volumen!
Das Volumen des Kegels beträgt ca. .
Hast du eine Frage oder Feedback?
Schau dir den Artikel zum Kegel an und suche die passende Formel für das Volumen heraus.
Berechne den Oberflächeninhalt des Kegels.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Kegel
In der Formel haben wir alle Werte gegeben außer die Mantellinie .
Berechnung der Mantellinie
Die Mantellinie erhältst du ähnlich wie die Höhe in der Teilaufgabe über das rechtwinklige Dreieck.
Benutze wieder eine trigonometrische Funktion, um die Mantellinie zu berechnen!
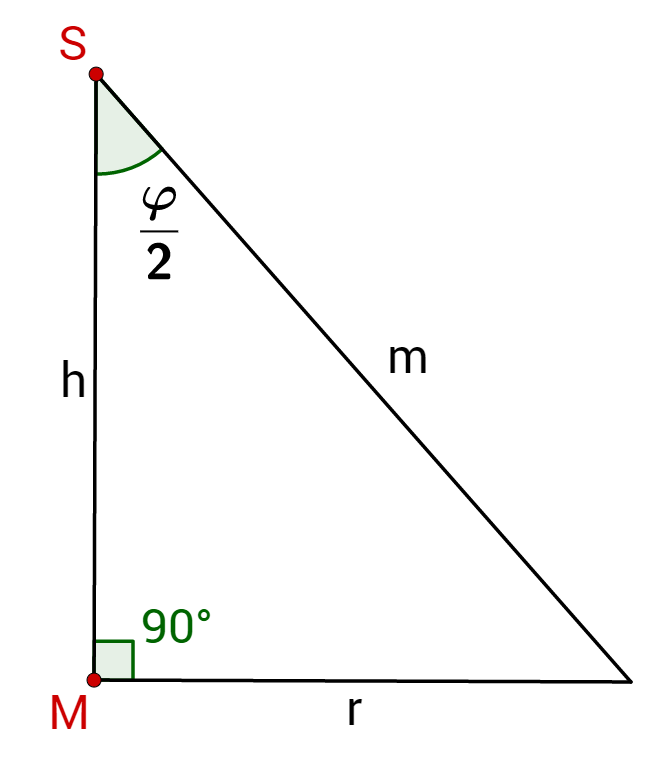
Nutze den Sinus um mithilfe von und zu berechnen. Und stelle die Gleichung entsprechend um!
Setze die Werte für und ein und berechne die Mantellinie .
Die Mantelfläche ist lang.
Berechnung des Oberflächeninhalts
Nutze die Formel für den Oberflächeninhalt des Kegels und setze die Werte ein.
Die Oberfläche des Kegels beträgt ca. .
Hast du eine Frage oder Feedback?
Den Oberflächeninhalt des Kegels erhältst du mithilfe einer Formel, die du im Artikel zum Kegel findest.
Zeichne ein sauberes Bild des Netzes von diesem Kegel.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Kegel
Vorüberlegungen
Beginne mit einer Skizze, in die du alle wichtigen Werte einzeichnest, die du kennen musst bevor du starten kannst.
Skizze:

In der nebenstehenden Skizze kennst du die Werte für und , dir fehlt aber der Wert für .
Die Mantelfläche um ist ein Kreissektor. Schau dir dazu nochmals die Formeln an und versuche den Wert für den Mittelpunktswinkel zu berechnen.
Der Mittelpunktswinkel berechnet sich folgendermaßen in einem Kreissektor:
Mit ist die Fläche gemeint, die ein Kreis mit dem Radius hätte.
Stelle jetzt die Flächen und auf und setze sie in die Formel ein.
Tipp: entspricht der Mantelfläche des Kegels.
Kürzen ergibt:
Stelle die Gleichung nach um!Und setze die Werte ein.
Dieser Kegel hat einen Mittelpunktswinkel seiner Mantelfläche von .
Konstruktion des Kegel - Netzes
Beginne mit der Mantelfläche und zeichne dazu den Mittelpunktswinkel an den Punkt der Spitze .
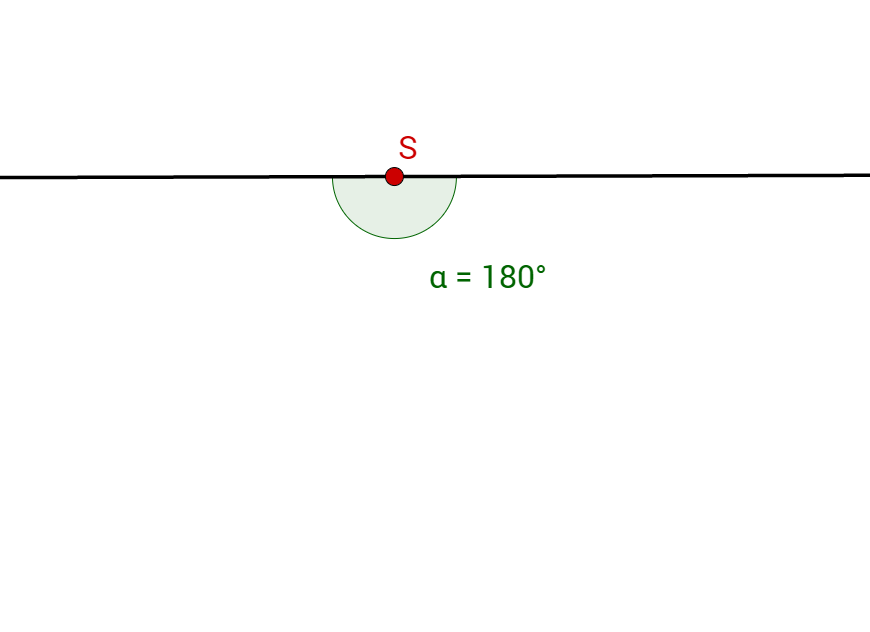
Zeichne einen Halbkreis mit dem Radius um den Punkt .
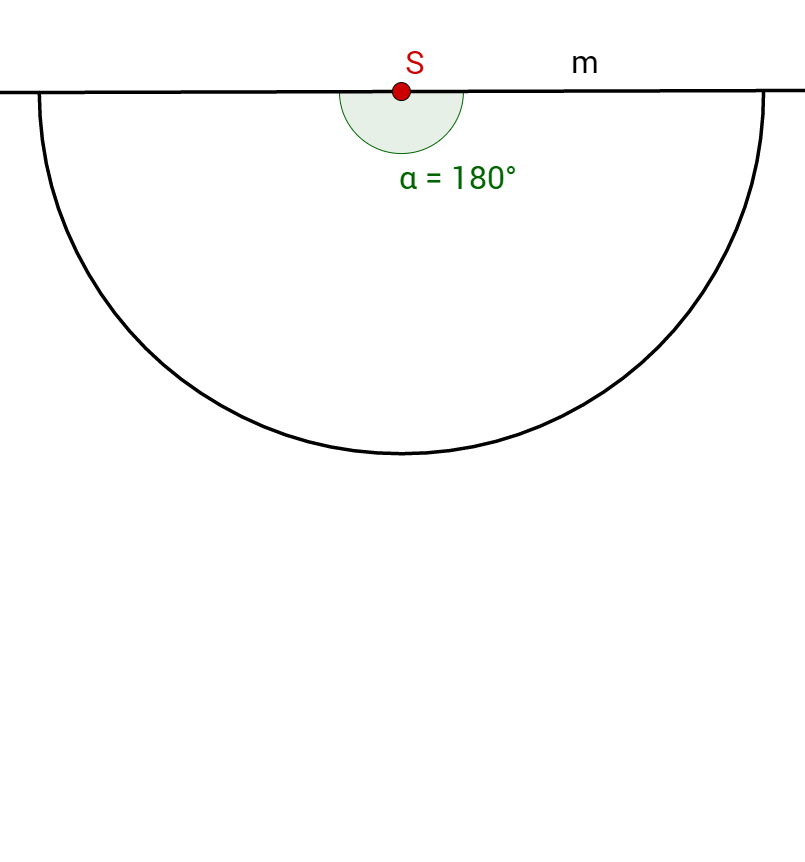
Suche dir einen beliebigen Punkt am Halbkreis, an dem die Grundfläche des Kegels die Mantelfläche berührt. Benenne ihn! Zum Beispiel mit .
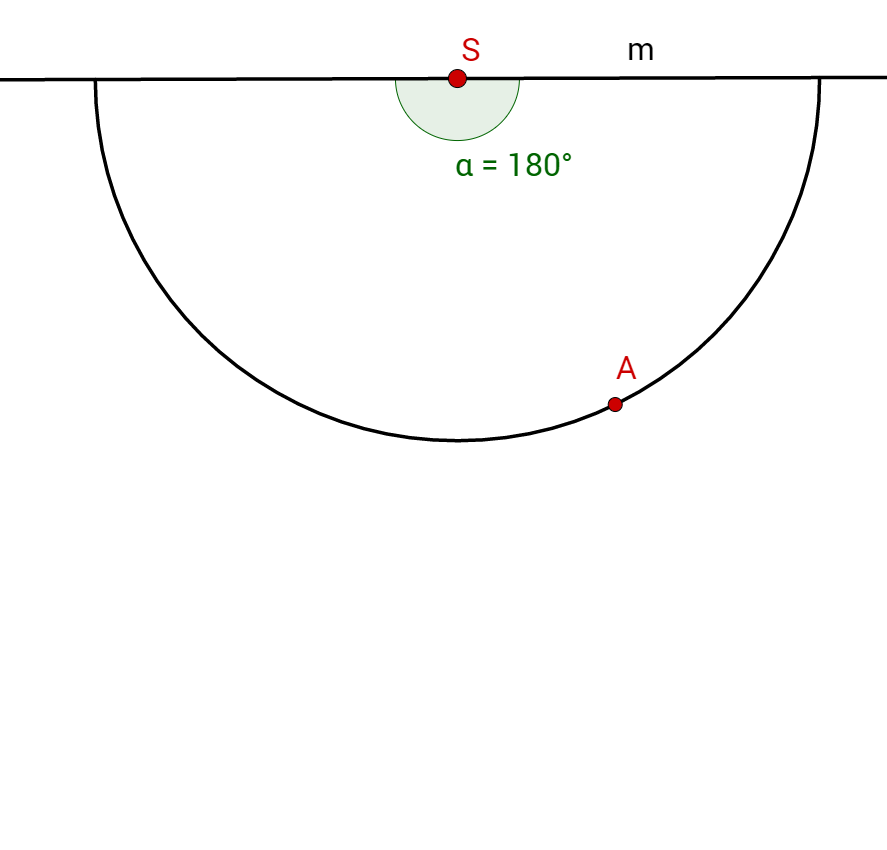
Verbinde den Punkt mit dem Punkt durch eine Halbgerade!
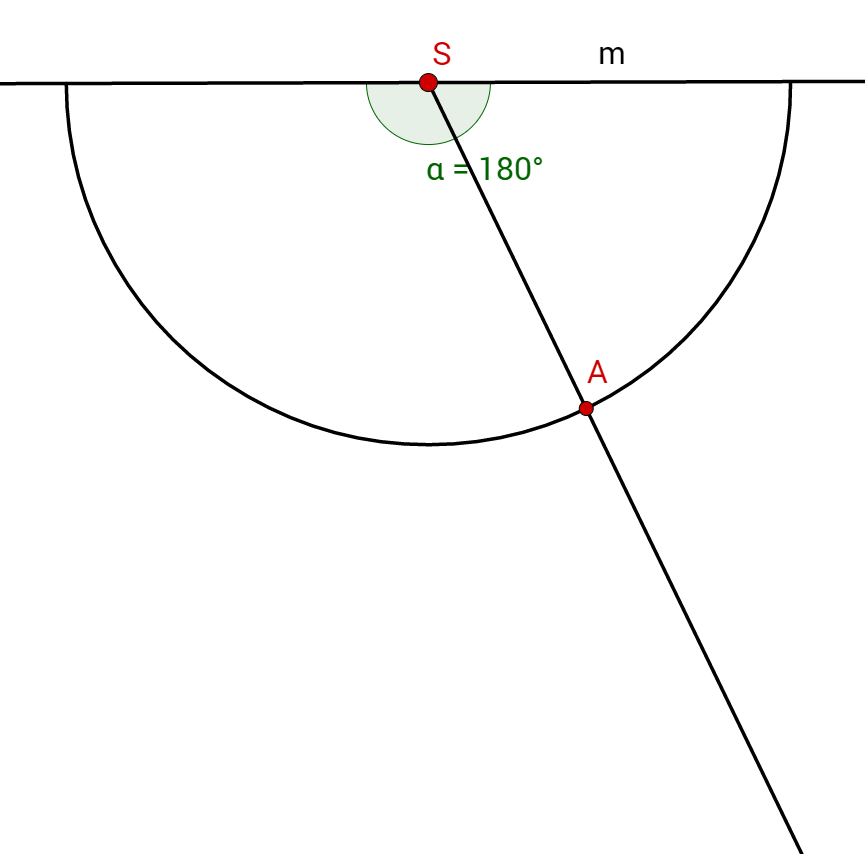
Am Punkt trägst du nun den Radius ab und erhältst einen Schnittpunkt mit der Halbgerade.
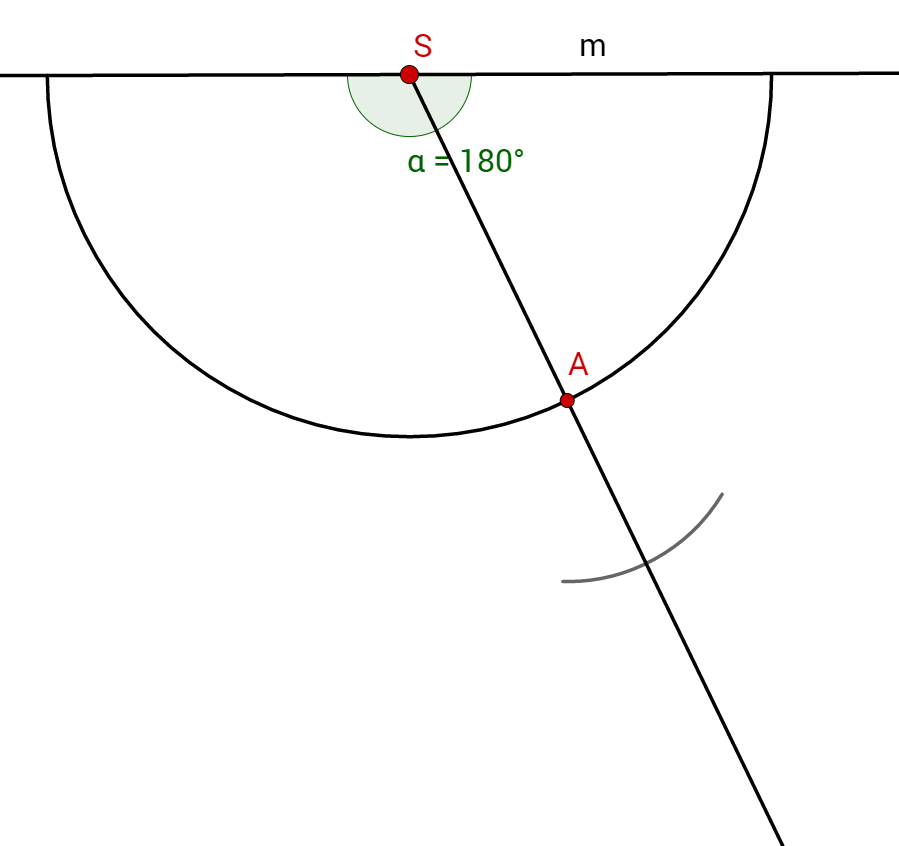
Dieser Schnittpunkt ist (Mittelpunkt der Grundfläche).
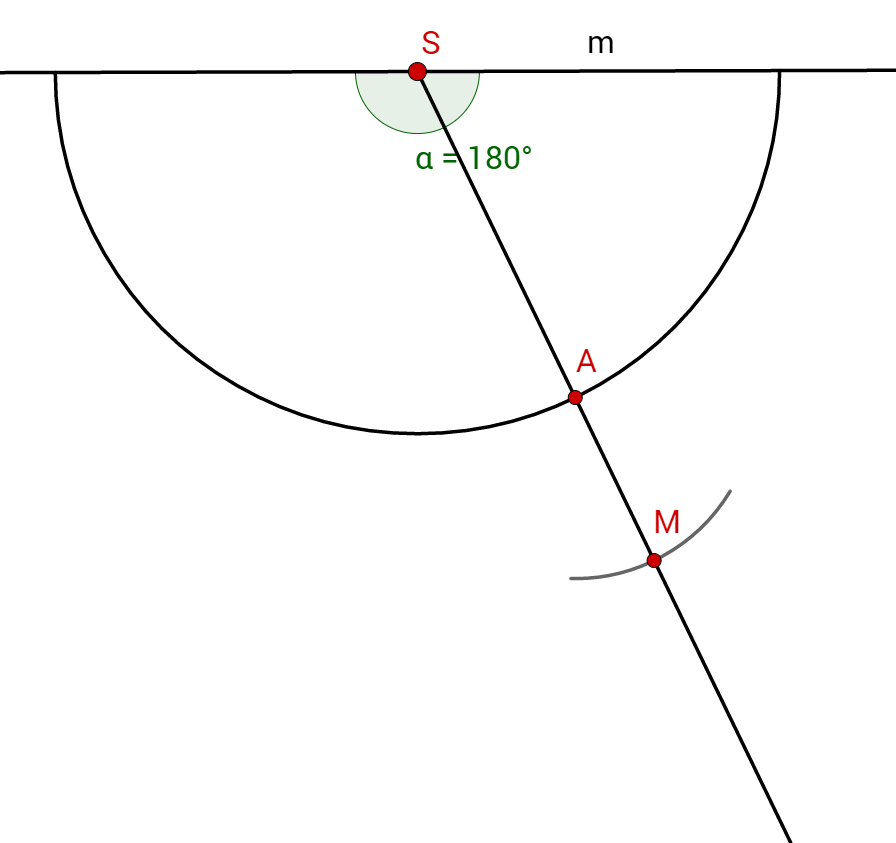
Wenn du um den Kreis mit zeichnest hast du die Grundfläche.

Die türkis eingefärbte Fläche ist das Netz des Kegels.
Hast du eine Frage oder Feedback?
Tipp: Im Artikel zum Kegel ist ein Bild des Netzes vom Kegel zu sehen. Überlege dir, wie es für deinen Kegel aussehen muss!
Benutze für die aus der Angabe in deinem Heft.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
