Die sogenannte Mantellinie gibt es bei Rotationskörpern wie Kegel und Zylinder. Mantellinien sind jene die Linien, die vom höchsten zum tiefsten Punkt an den Außenseiten liegen. In diesem Artikel findest du Formeln zur Berechnung dieser Längen und Grafiken zur Veranschaulichung.
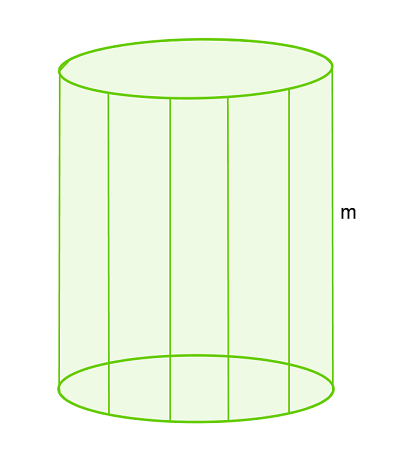
Mantellinien eines Zylinders
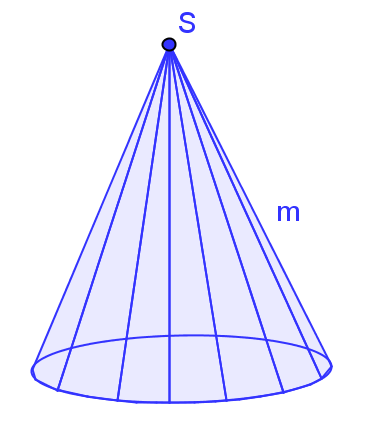
Mantellinie beim Kegel
Die Mantellinie m ist die Strecke von einem Punkt auf der Kreislinie der Grundfläche zur Spitze. Du berechnest die Länge der Linie wie folgt:
r ist Radius der Grundfläche,
h ist der Abstand von s zur Grundfläche
Dies lässt sich aus dem Satz des Pythagoras herleiten.
Mantellinie m beim Zylinder:
Die Mantellinie m des Zylinders ist die senkrechte Strecke von der Grund- zur Deckfläche auf der Manteloberfläche.
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
