Berechne das Volumen eines Kegelstumpfs mit Höhe , Grundflächenradius und Deckelradius .
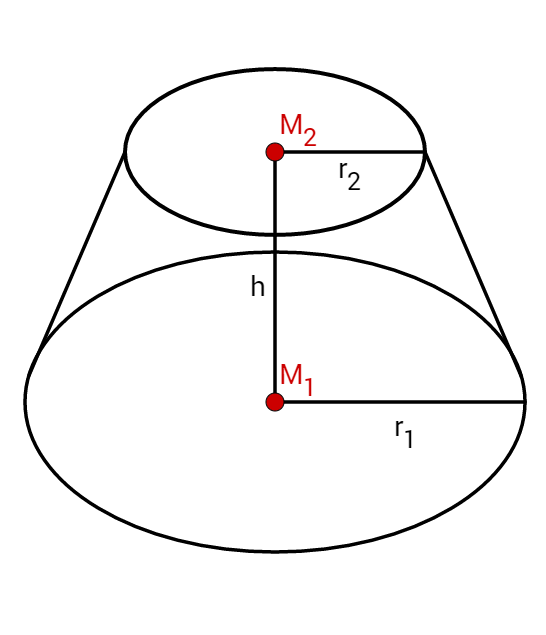
Für diese Aufgabe benötigst Du folgendes Grundwissen: Volumen eines Kegels
Volumen eines Kegelstumpfes berechnen
Um das Volumen eines solchen Kegelstumpfes zu berechnen, musst du dir vorstellen, dass der Kegel nicht "abgeschnitten" ist, sondern noch seine charakteristische Spitze hat. Dann kann man das gesamte Volumen dieses Kegels berechnen und die Spitze wieder abziehen. Zeichne dazu zuerst eine Skizze des gesamten Kegels!
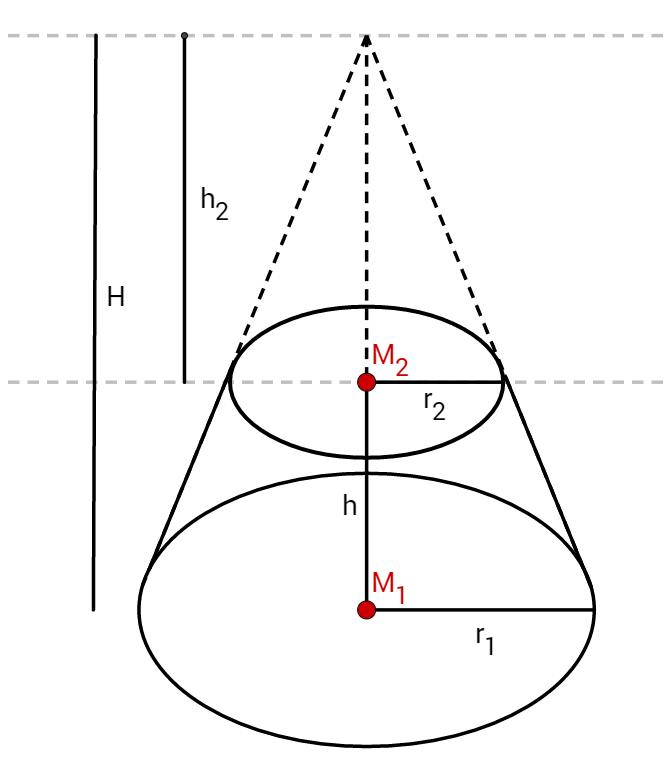
Deine Skizze sollte ungefähr so aussehen. Wichtig sind die Höhen.
ist die Höhe des gesamten Kegels, ist die Höhe der "imaginären" Spitze.
Jetzt musst du zuerst auf die Höhe kommen, dafür machst du am besten einen Querschnitt des Kegels.
Berechnung der Höhen und
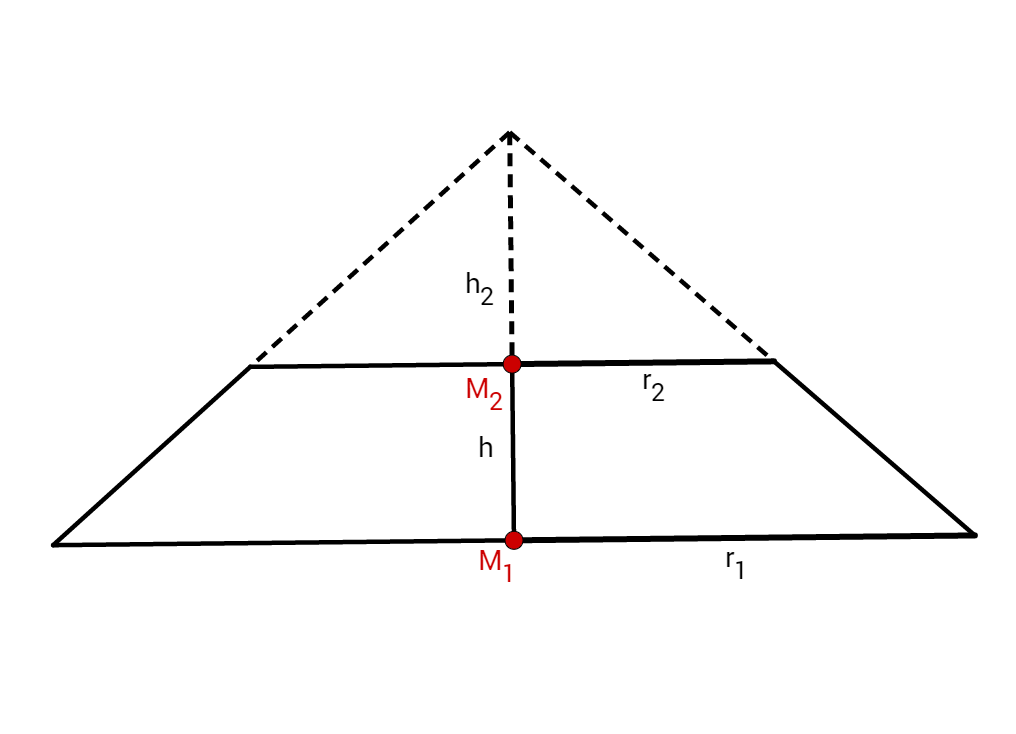
Bei dieser Skizze siehst du, dass es ausreichend ist, nur die rechte Seite des Dreiecks zu betrachten. Außerdem kannst du eine senkrechte Linie auf einzeichnen, die genau auf den Endpunkt von trifft.

Die rechte Seite deines Querschnitts sollte ungefähr so aussehen.
Du hast nun die Verbindungslinie von und eingezeichnet (gestrichelt) und erhältst dadurch einen Abschnitt von mit .
Außerdem kannst du zwei ähnliche Dreiecke erkennen. Einmal das Dreieck rechts unten mit , und und dann noch das Dreieck oben mit , und .
Versuche nun die bekannten Strecken einzuzeichnen und den Winkel zu bestimmen!
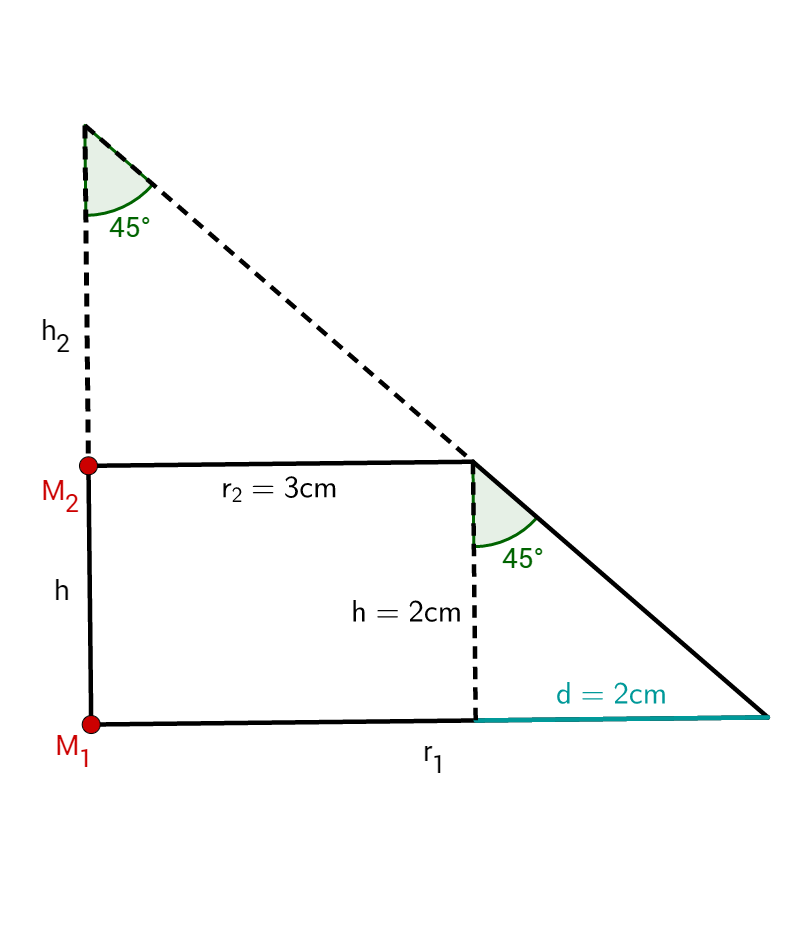
Das rechte untere Dreieck hat die Längen und
.
Damit hast du ein gleichschenkliges und rechtwinkliges Dreieck. Bei einem gleichschenkligen Dreieck hast du immer zwei gleiche Winkel und du hast zusätzlich noch einen Winkel.
Dadurch kommst du auf:
Und erhältst: .
Durch eine Ähnlichkeitsbetrachtung kannst du nun auch berechnen.
Da du zwei ähnliche Dreiecke hast, muss das obere Dreieck auch gleichschenklig sein. Dadurch erhältst du:
Berechne nun die gesamte Höhe des Kegels und das Volumen des ganzen Kegels mit dem Radius und der Höhe .
Berechnung des gesuchten Volumens
Von dem Gesamtvolumen ziehst du nun das Volumen des "imaginären" Kegels mit der Höhe und dem Radius ab und erhältst so das Volumen des Kegelstumpfs .
Das Volumen des Kegelstumpfs beträgt .
Ergänze den Kegelstumpf, so dass ein vollständiger Kegel entsteht dessen Volumen du berechnen kannst. Ziehe anschließend das Volumen der "imaginären" Kegelspitze wieder ab!
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
