Flächeninhalt und bestimmtes Integral

…

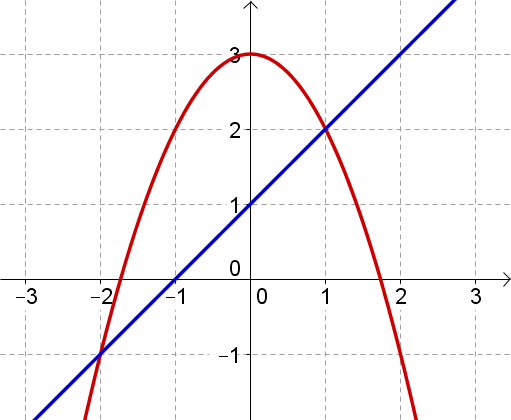
Die abgebildete Parabel $f$ und Gerade $g$ schließen eine Fläche mit dem Inhalt $A$ ein.

Schraffiere diese Fläche.

Bestimme die Funktionsterme von $f$ und $g$ und die beiden Schnittpunkte $S_{1}$ und $S_{2}$ der Graphen.

Gib $A$ als bestimmtes Integral an und berechne dann $A$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen

Berechnung des zur Parabel $f$ gehörenden Funktionsterms:

Der Scheitel der Parabel kann abgelesen werden: $S (0 ∣ 3)$

$f (x) = a (x - 0)^{2} + 3 = a x^{2} + 3$

Weiterhin kann der Punkt $(- 2 | - 1)$ abgelesen werden.

Setze den Punkt $(- 2 | - 1)$ in $f (x) = a x^{2} + 3$ ein:

Die Parabel hat die Funktionsgleichung $f (x) = - x^{2} + 3$

Die Geradengleichung kann direkt abgelesen werden:

(Steigung $m = 1$ und der y-Achsenabschnitt $t = 1$ ):

$g (x) = x + 1$

Setze $f (x) = g (x)$ .

$- x^{2} + 3$	$=$	$x + 1$	$+ x^{2}$
	↓	Bringe alle Terme auf eine Seite.
$3$	$=$	$x^{2} + x + 1$	$- 3$
$0$	$=$	$x^{2} + x - 2$

Die Lösung dieser quadratischen Gleichung erfolgt mit der pq-Formel (oder auch mit der Mitternachtsformel).

Lies $p$ und $q$ ab:

$p = 1$ und $q = - 2$

Damit ist $x_{1} = - 2$ und $x_{2} = 1.$

Setze beide Werte z.B. in $g (x)$ ein, um die Funktionswerte der beiden Schnittpunkte zu erhalten:

$g (- 2) = - 2 + 1 = - 1 \Rightarrow S_{1} (- 2 | - 1)$

$g (1) = 1 + 1 = 2 \Rightarrow S_{2} (1 | 2)$

Die beiden Schnittpunkte $S_{1}$ und $S_{2}$ der Graphen sind $S_{1} (- 2 | - 1)$ und $S_{2} (1 | 2)$ .

$A$	$=$	$\int_{- 2}^{1} (f (x) - g (x)) d x$
	↓	Setze $f (x)$ und $g (x)$ ein.
	$=$	$\int_{- 2}^{1} (- x^{2} + 3 - (x + 1)) d x$
	↓	Löse die Klammer auf und fasse zusammen.
	$=$	$\int_{- 2}^{1} (- x^{2} - x + 2)) d x$
	$=$	${[- \frac{1}{3} x^{3} - \frac{1}{2} x^{2} + 2 x]}_{- 2}^{1}$
	$=$	$(- \frac{1}{3} \cdot 1^{3} - \frac{1}{2} \cdot 1^{2} + 2 \cdot 1) - (- \frac{1}{3} \cdot (- 2)^{3} - \frac{1}{2} \cdot (- 2)^{2} + 2 \cdot (- 2))$
	↓	Löse die Klammern auf
	$=$	$- \frac{1}{3} - \frac{1}{2} + 2 - \frac{8}{3} + 2 + 4$
	↓	Fasse zusammen.
	$=$	$8 - \frac{9}{3} - 0,5$
	$=$	$8 - 3 - 0,5$
	$=$	$4,5$

Die beiden Graphen schließen eine Fläche mit dem Inhalt $A = 4,5 FE$ ein.