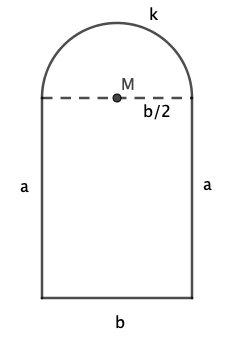
Eine romanische Fensterform ist zusammengesetzt aus einem Rechteck und einem oben anschließenden Halbkreis.
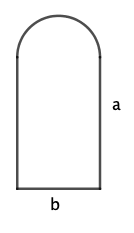
Das nebenstehende romanische Fenster habe den Umfang und die Rechtecksseiten und .
Bei welchen Werten für und hat das Fenster den größtmöglichen Flächeninhalt?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 mit Namensnennung von Herrn Günther Rasch → Was bedeutet das?