Aufgaben zu Extremwertproblemen aus der Geometrie

Hier findest du Aufgaben zu Extremwertproblemen aus der Geometrie. Schaffst du sie alle?

1
raschweb.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Günther Rasch
Auf einem Bauernhof möchte der Bauer eine rechteckige Koppel für seine Pferde anlegen.
Die Koppel liegt an einem Fluss und soll deshalb nur an drei Seiten eingezäunt werden.
Der zur Verfügung stehende Zaun ist 120m lang.
Wie muss der Bauer die Koppel anlegen, damit sie eine möglichst große Weidefläche hat?
Wie groß ist die Weidefläche dieser Koppel?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgabe zur Berechnung einer maximalen Weidefläche
Gegeben: kombinierte Länge von drei Seiten
Gesucht: ideale Seitenlänge für maximale Fläche
$A=l\cdot b$
Bestimme die Zielfunktion, nämlich die Fläche eines Rechtecks mit den Seitenlängen $a$ und $b$
$2\cdot b+l=120$
Stelle die Nebenbedingung auf. Da man für eine Seite (z. B. l) keinen Zaun benötigt, verändert sich die Nebenbedingung im Vergleich zur normalen Umfangsformel $U=2\left(l+b\right)$ etwas.
$A(b)=(120-2b)\cdot b=120b-2b^2$
mit $b > 0$
Setze die Nebenbedingung in die Zielfunktion ein und erhalte die Extremalfunktion. Beachte dabei, dass b sinnvollerweise nur positive Werte annehmen kann.
$A^{'} (b) = 120 - 4 b$
$A^{''} (b) = - 4$
Leite die Extremalfunktion zweimal ab, um im nächsten Schritt den Extremwert und die Art des Extremwertes bestimmen zu können.
$A^{'} = 120 - 4 b = 0$
$120 = 4 b$
$b = 30$
Setze die erste Ableitung gleich Null und setze die Lösung dieser Gleichung in die zweite Ableitung ein. Du erkennst dann, dass der Extremwert tatsächlich wie gewünscht ein Maximum ist.
$l=120-2\cdot30=60$
$A=60\cdot30=1800$
Berechne nun noch $l$ durch Einsetzen der Breite $b$ in die Nebenbedingung und die Fläche der Weidekoppel.
Für die maximale Weidefläche muss der Bauer die Koppel also 60 m lang und 30 m breit wählen. Damit erreicht er eine Weidefläche von 1800 m².

Die Gemeinde Haar weist neues Bauland aus.

Herr Meier hat die dreieckige Fläche gekauft, muss aber nun (wie vorgeschrieben) ein rechteckiges Baugrundstück festlegen.

Wie sollte sich Herr Meier entscheiden, wenn er ein möglichst großes Baugrundstück haben will?

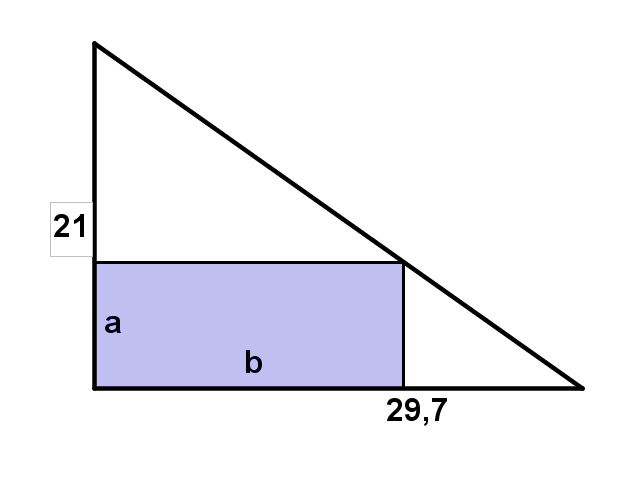
Aus einem diagonal halbierten DIN A4 Blatt soll entsprechend der Zeichnung ein möglichst großflächiges Rechteck geschnitten werden.

Finde die Breite a, für die der Flächeninhalt des Rechtecks maximal ist.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgabe

Stelle die allgemeine Flächenformel eines Rechtecks auf.

$\mathrm A=\mathrm a\cdot\mathrm b$

Bestimme b. Benutze dazu, dass das ganze Dreieck ähnlich zu dem schraffierten Dreieck ist und berechne mit dem SWS-Satz (oder: Strahlensatz V-Figur) die Seite b.

$\displaystyle \frac{\mathrm{b}}{\left(21-\mathrm{a}\right)}$	$=$	$\displaystyle \frac{29{,}7}{21}$
	↓	Löse nach b auf.
$\displaystyle b$	$=$	$\displaystyle \frac{29{,}7}{21}\cdot\left(21-\mathrm{a}\right)$
	↓	Setze b in die allgemeine Form für den Flächeninhalt des Rechtecks ein.
$\displaystyle A$	$=$	$\displaystyle \mathrm{a}\cdot\frac{29{,}7}{21}\cdot\left(21-\mathrm{a}\right)$
	$=$	$\displaystyle \mathrm{a}\left(29{,}7-\frac{29{,}7}{21}\mathrm{a}\right)$
	$=$	$\displaystyle 29{,}7\mathrm{a}-\frac{29{,}7}{21}\mathrm{a}^2$

Dies ist nun die Formel für den Flächeninhalt des Rechtecks in Abhängigkeit von a.

Bestimme nun den maximalen Flächeninhalt.

Da es sich um eine nach unten geöffnete Parabel handelt, liegt das Maximum der Funktion bei ihrem Scheitelpunkt .

Dieser liegt genau in der Mitte zwischen den beiden Nullstellen.

Bestimme die Nullstellen der Funktion.

$\displaystyle -\frac{29{,}7}{21}\mathrm{a}^2+29{,}7\mathrm{a}$	$=$	$\displaystyle 0$
$\displaystyle \mathrm{a}\left(29{,}7-\frac{29{,}7}{21}\mathrm{a}\right)$	$=$	$\displaystyle 0$

Betrachte die beiden Faktoren getrennt. Betrachte zuerst den 1. Faktor:

$\Rightarrow\;\;{\mathrm a}_1=0$

Betrachte den 2. Faktor:

$\displaystyle 29{,}7-\frac{29{,}7}{21}\mathrm{a}$	$=$	$\displaystyle 0$	$\displaystyle +\frac{29{,}7}{21}a$
$\displaystyle 29{,}7$	$=$	$\displaystyle \frac{29{,}7}{21}\mathrm{a}$	$\displaystyle :\frac{29{,}7}{21}$

$\Rightarrow\;\;{\mathrm a}_2=21$

Bestimme die Stelle, an der der Scheitelpunkt liegt (Mitte der Nullstellen).

$\Rightarrow$ Scheitel bei $\mathrm a=10{,}5$

Formuliere einen Antwortsatz.

Für $\mathrm a=10{,}5$ wird der Flächeninhaltdes Rechtecks maximal.

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.

4
raschweb.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Günther Rasch
Aus einem $36\,\mathrm{m}$ langen Draht soll das Kantenmodell einer quadratischen Säule hergestellt werden.
Wie lang sind die Kanten zu wählen, damit die Säule maximales Volumen hat?
ist die Kantenlänge.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgabe
Gegeben: Gesamtkantenlänge einer quadratischen Säule
Gesucht: Kantenlängen für maximales Volumen
$V=a^2\cdot h$
Stelle die Zielfunktion auf, die maximiert werden soll; in diesem Fall ist das das Volumen einer quadratischen Säule mit der Grundseitenlänge $a$ und der Höhe $h$ .
$4\cdot a+4\cdot h+4\cdot a=36$
Bestimme die Nebenbedingung, die durch die Gesamtkantenlänge gegeben ist.
$h = 9 - 2 a$
Stelle die Nebenbedingung nach $h$ um.
$V(a)=a^2\cdot\left(9-2a\right)$ mit $a > 0$
Setze die Nebenbedingung in die Zielfunktion ein, um die Extremalfunktion zu erhalten. Beachte dabei, dass a positiv sein muss. Leite die Extremfunktion zweimal ab.
$\def\arraystretch{1.25} \begin{array}{ccc}V'(a)&=&18a-6a^2\\V''(a)&=&18-12a\end{array}$
Setze die erste Ableitung gleich Null, berechne die Grundseitenlänge und setze ihn in die zweite Ableitung ein, um zu erkennen, dass es sich tatsächlich um ein Maximum handelt.
$V^{'} (a) = 18 a - 6 a^{2} = a (18 - 3 a) = 0$
$a = 0$ oder $a = 3$
$a = 0$ muss nicht weiter untersucht werden, da nur positive Grundseitenlängen betrachtet werden.
$\def\arraystretch{1.25} \begin{array}{l}V''(3)=18-12\cdot3=-18<0\\\end{array}$
Da die zweite Ableitung negativ ist, handelt es sich bei $a = 3$ um das gesuchte Maximum.
Gib nun endgültig $a$ und $h$ an und berechne das Volumen (nicht verlangt).
$a=3\;\Rightarrow h=3\Rightarrow V=27$
5
raschweb.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Günther Rasch
Aus einem 120cm langen Draht ist das Kantenmodell eines Quaders herzustellen, so dass eine Kante dreimal so lang wie eine andere und der Rauminhalt maximal ist.
Wie lang sind die Kanten zu wählen?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgabe
Gegeben: Gesamtkantenlänge, eine Kante dreimal so lang wie eine andere Kante
Gesucht: Kantenlänge so, dass Volumen maximal
Stelle die Volumenfunktion des Quaders mit den Kanten $a$ , $b$ und $c$ auf; das ist die Zielfunktion, die es zu maximieren gilt.
$V=a\cdot b\cdot c$
Bestimme die Nebenbedingung, welche durch die Gesamtkantenlänge und die Tatsache, dass eine Kante dreimal so lang wie eine andere Kante sein soll, gegeben ist. Wähle dabei z. B. b=3a.
$4\cdot a+4\cdot3\cdot a+4\cdot c=120$
Stelle die Nebenbedingung um.
$c = 30 - 4 a$
Setze die Nebenbedingung in die Zielfunktion ein und erhalte die Extremalfunktion. Beachte dabei, dass negative Längen keinen Sinn machen.
$V(a)=3\cdot a^2\cdot(30-4a)$ mit $a > 0$
Leite die Extremalfunktion zweimal ab, um im nächsten Schritt den Extremwert und die Art des Extremwertes bestimmen zu können.
$\def\arraystretch{1.25} \begin{array}{ccc}V'(a)&=&180a-36a^2\\V''(a)&=&180-72a\end{array}$
Setze die erste Ableitung gleich Null und setze die Lösung dieser Gleichung in die zweite Ableitung ein. Du erkennst dann, dass der Extremwert tatsächlich wie gewünscht ein Maximum ist.
$V^{'} (a) = 0$
$a = 5$
$V^{''} (5) = - 180 < 0$
Berechne nun noch die Kantenlängen $b$ und $c$ .
$\def\arraystretch{1.25} \begin{array}{l}\;\;\;\;\;\;a=5\\\Rightarrow b\;=3\cdot5=15\\\Rightarrow c\;=30-4\cdot5=10\end{array}$
Kante $a$ ist $5 c m$ , Kante $b$ $15 c m$ und Kante $c$ $10 c m$ zu wählen.
6
Eine oben offene zylinderförmige Dose mit dem Volumen V soll aus Blech hergestellt werden. Dabei soll der Blechverbrauch möglichst gering sein. Bestimme die Höhe und den Durchmesser der Dose, sowie den minimalen Blechverbrauch.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung
Wir suchen aus allen Konservendosen mit Volumen V diejenige mit minimalem Oberflächeninhalt.
Volumenformel: $\mathrm V=\mathrm G\cdot\mathrm h$ (Grundseite mal Höhe) wobei die Grundseite eines Zylinders ein Kreis ist, d.h. ${\mathrm G}_\mathrm{Kreis}=\mathrm r^2\cdot\mathrm\pi$ .
Oberflächeninhalt eines Zylinders ist gegeben durch ${\mathrm A}_\mathrm{Zylinder}=A_{Mantel}+A_{Kreis}=2\cdot\mathrm r\cdot\mathrm\pi\cdot\mathrm h+\mathrm r^2\cdot\mathrm\pi$ .
Zielfunktion bestimmen: Der Oberflächeninhalt des Zylinders ist zu minimieren. Unsere Funktion ist von r und h abhängig. ${\mathrm A}_\mathrm{Zylinder}=2\cdot\mathrm r\cdot\mathrm\pi\cdot\mathrm h+\mathrm r^2\cdot\mathrm\pi$ .
Nebenbedingungen formulieren und einsetzen: Der Oberflächeninhalt des Zylinders ist zu minimieren unter der Bedingung, dass das Volumen erhalten bleibt. Wir können nun also die Höhe in Abhängkeit vom Radius ermitteln, indem wir die Formel $\mathrm V={\mathrm G}_\mathrm{Kreis}\cdot\mathrm h=\mathrm r^2\cdot\mathrm\pi\cdot\mathrm h$ nach h auflösen. Es ergibt sich die Nebenbedingung $h=\frac V{r^2\cdot\mathrm\pi}$ . Einsetzen in die Zielfunktion ergibt: $\mathrm A=2\cdot\mathrm r\cdot\mathrm\pi\cdot{\textstyle\left({\displaystyle\frac{\mathrm V}{\mathrm r^2\cdot\mathrm\pi}}\right)}+r^2\cdot\mathrm\pi=2\cdot\frac Vr+r^2\cdot\mathrm\pi=2V\cdot\frac1r+\mathrm\pi\cdot\mathrm r^2$ . Unsere Zielfunktion hängt jetzt nur noch von r ab, also können wir auch schreiben $\mathrm A(\mathrm r)=2\mathrm V\cdot\frac1{\mathrm r}+\mathrm\pi\cdot\mathrm r^2$ .
Für die Extremalfunktion $\mathrm A(\mathrm r)$ den Definitionsbereich $\mathbb{D}_\mathrm A$ bestimmen: $\mathbb {D}_A=\mathbb{R}\backslash\{0\}$ . Allerdings muss r > 0 sein.
Wir suchen das Minimum von $\mathrm A(\mathrm r)$ mit Hilfe der ersten und zweiten Ableitung.
Erste Ableitung
$(\frac1r)'=-\frac1{\mathrm r^2}$
$\left(\mathrm r^2\right)'=2\mathrm r$
$\Rightarrow A'(r)=2V\cdot\left(-\frac{1}{r^2}\right)+\mathrm{\pi}\cdot2r$
Zweite Ableitung
$(\frac1r)''=\frac2{r^3}$
$\left(\mathrm r^2\right)''=\left(2\mathrm r\right)`=2$
$\Rightarrow A''(r)=2V\cdot\left(2\cdot\frac1{r^3}\right)+\mathrm\pi\cdot2$
Für ein mögliches Minimum muss die erste Ableitung gleich Null werden. Setze also $A'\left(r\right)=2V\cdot\left(-\frac{1}{r^2}\right)+\pi\cdot2r$ gleich $0$ .
$\def\arraystretch{1.25} \begin{array}{rcll}A'(r)&=&0\\2V\cdot\left(-\frac{1}{r^2}\right)+\mathrm{\pi}\cdot2r&=&0\\-\frac{2V}{r^2}+\mathrm{\pi}\cdot2r&=&0&|+\frac{2V}{r^2}\\2\pi r&=&\frac{2V}{r^2}&|\cdot r^2\\2\pi r^3&=&2V&|:2\pi\\r^3&=&\frac V\pi&|\sqrt[3]{}\\r&=&\sqrt[3]{\frac V \pi}\end{array}$
Einsetzen in die 2. Ableitung ergibt:
$A''(\sqrt[3]{\frac V{\mathrm\pi}})=2V\cdot\left(2\cdot\frac1{\left(\sqrt[3]{\displaystyle\frac V{\mathrm\pi}}\right)^3}\right)+\mathrm\pi\cdot2=\underbrace{4V\cdot\frac{\mathrm\pi}V}_{=4\cdot\mathrm\pi}+2\cdot\mathrm\pi=6\cdot\mathrm\pi>0$
Also liegt tatsächlich ein Minimum vor an dieser Stelle.
Lösung
Den minimale Oberflächeninhalt erhält man für die Dose mit dem Radius $\mathrm{r}_{\min}=\sqrt[3]{\frac{\mathrm{V}}{\mathrm{\pi}}}$ . Also ist der Durchmesser $\mathrm d=2\mathrm r=2\sqrt[3]{\frac{\mathrm V}{\mathrm\pi}}$ . Die Höhe h erhält man aus der Nebenbedingung $h=\frac V{r^2\cdot\mathrm\pi}$ durch einsetzen von $\mathrm{r}_{\min}$ , also
$h=\frac V{\sqrt[3]{\left({\displaystyle\frac{\mathrm V}{\mathrm\pi}}\right)^2}\cdot\mathrm\pi}=\frac{\sqrt[3]{V^3}}{\sqrt[3]{\displaystyle\frac{V^2}{\mathrm\pi^2}}\cdot\sqrt[3]{\mathrm\pi^3}}=\sqrt[3]{\frac{V^3}{V^2\cdot\mathrm\pi}}=\left(\sqrt[3]{\frac V{\mathrm\pi}}\right)$
Der minimale Oberflächeninhalt ist $3\mathrm\pi\cdot\left(\sqrt[3]{\frac{\mathrm V}{\mathrm\pi}}\right)^2$ (Einsetzen in die Zielfunktion.)

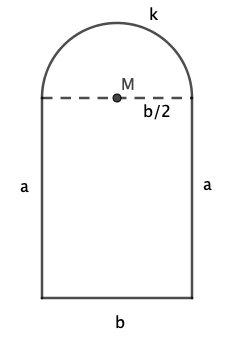
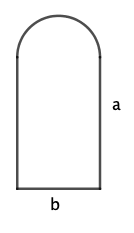
Eine romanische Fensterform ist zusammengesetzt aus einem Rechteck und einem oben anschließenden Halbkreis.

Das nebenstehende romanische Fenster habe den Umfang $u\,=\,5\,LE$ und die Rechtecksseiten $a\,LE$ und $b\,LE$ .

Bei welchen Werten für $a$ und $b$ hat das Fenster den größtmöglichen Flächeninhalt?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgaben

Für die Form eines romanischen Fensters (Rechteck mit oben angefügtem Halbkreis) soll bei gegebenem Umfang die größtmögliche Fläche berechnet werden.

Die Zielfunktion, deren Maximum zu berechnen ist, ergibt sich als Summe der Rechtecksfläche mit den Seitenlängen $a\,LE$ und $b\,LE$ und der Fäche des Halbkreises mit Radius $b/2\,LE$ .

Zielfunktion:

\displaystyle A(a;b)=a\cdot b+\frac12\cdot(\frac{b}{2})^2\pi

Der gegebene Umfang $u=5\,LE$ ist für die Zielfunktion die "Nebenbedingung".

Nebenbedingung

$2 a + b + k = 5$

Berechne $k$ als Kreisbogenlänge des Halbkreises.

$\displaystyle k$	$=$	$\displaystyle \frac{1}{2}\cdot2\cdot\left(\frac{b}{2}\right)\cdot\pi$
$\displaystyle k$	$=$	$\displaystyle \frac{1}{2}b\pi$
	↓	Setze $k$ in die Nebenbedingung ein und löse diese nach $a$ (oder auch nach $b$ ) auf.

$\begin {array} {r c l l}2a+b+\dfrac 12 b\pi&=&5&|\,\text{b ausklammern}\\2a+b(1+\dfrac 12 \pi)&=&5&|-\,b( …)\\2a&=&5-b(1+ \dfrac 12\pi)&|\;:2\\a&=&2{,}5-\dfrac 12 b(1+\dfrac 12 \pi)&\text{Setze a in A(a;b) ein.}\end{array}$

$\def\arraystretch{2} \begin{array}{rcl}A(\color{red}{b})&=&\color{red}{(}2{,}5-\dfrac12 b(1+\dfrac 12 \pi)\color{red}{)}\cdot b+ \dfrac 12\cdot (\dfrac {b}{2})^2\pi\\ &=&2{,}5b-\dfrac 12b^2(1+\dfrac12\pi)+\dfrac18b^2\pi&|\,\text{D-Gesetz für}\;\dfrac12b^2(1+\dfrac12\pi)\\ &=&2{,}5b-\dfrac12b^2-\dfrac14b^2\pi+\dfrac18b^2\pi&|\;b^2\,\text{zusammenfassen}\\&=&2{,}5b-b^2(\dfrac12+\dfrac14\pi-\dfrac18\pi)&|\text{zusammenfassen}\\A(b)&=&2{,}5b-(\dfrac12+\dfrac18\pi)b^2&|\,\text{Berechne A'(b) und A''(b)}.\end{array}$

$\displaystyle A´\left(b\right)$	$=$	$\displaystyle 2{,}5-b\left(1+\dfrac{1}{4}\pi\right)$
	↓	Setze $A^{'} (b)$ gleich Null und löse nach $b$ auf.
$\displaystyle A´´\left(b\right)$	$=$	$\displaystyle -1-\dfrac{1}{4}\pi\$
	↓	Da $A^{''} (b)$ für jedes $b$ negativ ist, ergibt sich ein Maximum.
$\displaystyle A´´\left(b\right)$	$<$	$\displaystyle 0$

$\def\arraystretch{2} \begin{array}{rcll}2{,}5-b(1+\dfrac14\pi)&=&0\\\displaystyle b\cdot\dfrac{4+\pi}{4}&=&2{,}5&|\;:\displaystyle \dfrac{4+\pi}{4}\\ b_{max}&=&\displaystyle \dfrac{10}{4+\pi}&\Rightarrow\end{array}$

$\def\arraystretch{2} \begin{array}{rcll}a_{max}&=&\displaystyle 2{,}5-\dfrac12\color{red}{(\dfrac{10}{4+\pi})}(1+\dfrac12\pi)\\&=&\displaystyle 2{,}5-\dfrac{5}{4+\pi}\cdot\dfrac{2+\pi}{2}\\&=&\displaystyle 2{,}5-2{,}5\cdot \dfrac{2+\pi}{4+\pi}\\&=&\displaystyle \dfrac{2{,}5\cdot (4+\pi)-2{,}5\cdot (2+\pi)}{4+\pi}\\a_{max}&=&\displaystyle \dfrac{5}{4+\pi}\end{array}$

Setze $b_{max}$ und $a_{max}$ in $A (a; b)$ ein, um die maximale Fläche des romanischen Fensters mit dem Umfang $5\,LE$ zu erhalten.

(Du kannst auch $b_{max}$ alleine in $A (b)$ einsetzen.)

$\def\arraystretch{2} \begin{array}{rcll}A_{max}&=&\displaystyle \dfrac{5}{4+\pi}\cdot \dfrac{10}{4+\pi}+\dfrac12 \cdot \left(\dfrac{5}{4+\pi}\right)^2\cdot \pi\\&=&\displaystyle\dfrac{50}{(4+\pi)^2}+\dfrac{25\pi}{2\cdot (4+\pi)^2}\\&=&\displaystyle \dfrac{100+25\pi}{2(4+\pi)^2}\\&=&\displaystyle \dfrac{25(4+\pi)}{2(4+\pi)^2}\\A_{max}&=&\displaystyle \dfrac{12{,}5}{4+\pi}\\A_{max}&\approx&1{,}75\end{array}$

Ergebnis:

Das romanische Fenster mit dem Umfang $5\,LE$ hat seine größte Fläche von rund $1{,}75\,FE$ , wenn die Grundseite gerade doppelt so groß ist wie die Höhe des Rechtecks.

Anhand des beigefügten Applets kannst du durch Verschieben des unteren rechten Eckpunkts das Ergebnis überprüfen.

Mit einem Klick auf Bild oder Button oben stimmst du zu, dass externe Inhalte von GeoGebra geladen werden. Dabei können persönliche Daten zu diesem Service übertragen werden – entsprechend unserer Datenschutzerklärung.

[https://www.geogebra.org/material/iframe/id/k9y5zucc]

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.

8
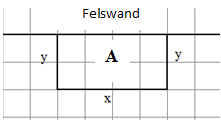
Ein Schäfer möchte für seine Schafe eine rechteckige Weidefläche mit einem Zaun begrenzen.
Die Weidefläche grenzt direkt an eine Felswand.
Der Schäfer hat insgesamt $40$ je $1 m$ lange zusammensteckbare Zaunelemente zur Verfügung.
Ermittle die Abmessungen $x$ und $y$ so, dass die abgesteckte Fläche einen maximalen Flächeninhalt $A$ hat.
Quellen
Abb 1: https://pixabay.com/de/schaf-berg-ranch-japan-zaun-680217/

Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitelpunktsform Extremum
Lösung zu a) mit Scheitelpunktsbestimmung
$A(x) = - 0{,}5 x^2 +20x$
Der Koeffizient vor dem $x^{2}$ ist negativ , somit handelt es sich um eine nach unten geöffnete Parabel. Der Scheitelpunkt ist ein Maximum.
Wir ermitteln die Scheitelpunktsform durch quadratische Ergänzung .
Klammere zuerst $(- 0,5)$ aus: $A(x) = (-0{,}5)\cdot (x^2 - 40x)$
Der gemischte Term in der Klammer ist $- 40 x$ , d.h. die quadratische
Ergänzung ist $(\dfrac{40}{2})^2 = 20^2$ .
Addiere in der Klammer $20^{2}$ und subtrahiere diesen Term gleich wieder:
$A(x) = (-0{,}5)\cdot (x^2 - 40x + 20^2 -20^2)$
Fasse die ersten drei Terme in der Klammer mit Hilfe der 2. binomischen Formel zusammen: $A(x) = (-0{,}5)\cdot ((x - 20)^2 -20^2)$
Löse die Klammer wieder auf:
$A(x) = (-0{,}5)\cdot (x - 20)^2+(-0{,}5)\cdot(-20^2)=(-0{,}5)\cdot (x - 20)^2+200$ Lies den Scheitelpunkt ab: $S(20\vert 200)$
Antwort: Die Länge des waagrechten Zaunstückes beträgt $x= 20\, \mathrm{m}$
und der maximale Flächeninhalt $200\, \mathrm{m^2}$ .
Es fehlt noch die Angabe der Zaunlänge $y$ .
Setze $x = 20$ in $y = 20-0{,}5\cdot x$ ein.
$y = 20-0{,}5\cdot 20 =20-10 = 10$ .
Antwort: Die Länge des senkrechten Zaunstückes beträgt $10\, \mathrm{m}$ .
Lösung zu b) mit der Ableitung
$$
$A(x) = - 0{,}5 x^2 +20x$
Der Definitionsbereich der Variablen $x$ ist das Intervall $0\lt x\lt40$ .
Für $ x = 0$ und für $x = 40$ erhält man ein "entartetes" Rechteck (mit dem Flächeninhalt $0\,\mathrm{m^2}$ ), d.h. eine Strecke der Länge $40\, \mathrm{m}$ .
Bedingung für ein Maximum: $A^{'} (x) = 0$ und $A''(x) \lt 0$
Die beiden Ableitungen lauten:
$A^{'} (x) = - x + 20$
$A^{''} (x) = - 1 < 0$
Setze $A^{'} (x)$ gleich Null: $0 = - x +20 \Rightarrow x=20$
$x = 20$ ist im Definitionsbereich von $A (x)$ enthalten.
Da $A''(x)<0_{ }$ ist, handelt es sich um ein Maximum.
Es fehlt noch die Angabe der zweiten Zaunlänge $y$ .
Setze $x = 20$ in $y = 20-0{,}5\cdot x$ ein: $y=20-0{,}5\cdot 20 = 20-10 = 10$
Nun kann die maximale Fläche berechnet werden: $A = x\cdot y=20\cdot 10 = 200.$
Antwort: Die Länge des waagrechten Zaunstückes beträgt $x= 20\, \mathrm{m}$ , die Länge des senkrechten Zaunstückes $y$ ist $10\, \mathrm{m}$ und der maximale Flächeninhalt beträgt $200\, \mathrm{m}^2$ .
Lösung:
Der Inhalt der Fläche $A$ ist sowohl von $x$ als auch von $y$ abhängig.
Zielfunktion : $A = x\cdot y$
Der Zaun soll eine Länge von $40 m$ haben, deshalb muss die Summe der Zaunteilstücke $40$ betragen.
Nebenbedingung: $x + 2 y = 40$
Die Nebenbedingung nach $y$ aufgelöst ergibt: $y = 20 – 0,5 x .$
Setzt man $y$ in die Zielfunktion ein, so erhält man den Flächeninhalt in Abhängigkeit von $x$ : $A(x) = x\cdot (20 – 0{,}5 x) = 20x – 0{,}5 x^2 = -0{,}5 x^2 +20x$
$A (x)$ ist nun eine quadratische Funktion der Rechtecksbreite $x$ .
Von dieser Funktion soll das Maximum bestimmt werden.
Dies kannst du auf folgende zwei Arten machen:
$a)$ mit Scheitelpunktsbestimmung und mit dem Wissen über quadratische Funktionen
$b)$ mit der Ableitung
9
Schultüten
Jana und Nish basteln zu ihrer Einschulung Schultüten.
Ihre Eltern haben ihnen bereits rundes dickes Papier bereit gelegt, mit einem Radius von $R=50\;\text{cm}$ .
Dieses malen sie bunt an und schneiden einen Kreissektor aus dem Papier aus, um einen Kegel zu formen.
Jana schneidet einen Kreissektor mit dem Mittelpunktswinkel $φ = 120 °$ aus. Nish wählt für seine Schultüte $\varphi=60°$ .
1. Jana ist der Meinung, dass in ihre Tüte doppelt so viel Inhalt passt wie in Nishs Tüte, da sie einen doppelt so großen Winkel gewählt hat. Berechne, ob Jana mit ihrer Annahme richtig liegt.
  Jana hat recht.
  Jana liegt falsch.
  
  Teillösung a)
  Das Volumen eines Kegels ist gegeben durch:
  $V=\frac{1}{3}\pi\cdot r^2\cdot h \;\;\; \mathrm{(I)}$
  Dabei ist $r$ der Radius des Kegelgrundkreises und $h$ die Höhe des Kegels.
  Die Bogenlänge $b$ des Kreissektors ist der Umfang des Kegelgrundkreises mit dem Radius $r$ .
  $\def\arraystretch{2} \begin{array}{rcl}b&=&\dfrac{R \cdot \pi \cdot \varphi}{180^\circ}\\\\ 2 \cdot \pi \cdot r &=&\dfrac{R \cdot \pi \cdot \varphi}{180^\circ}\\\\r&=&\dfrac{R \cdot \pi \cdot \varphi}{180^\circ \cdot 2 \cdot \pi}\\\\r &=&\dfrac{R \cdot \varphi}{360^\circ}\;\;\;\; \mathrm{(II)}\end{array}$
  Volumen von Nishs Schultüte
  Nish hat einen Kreissektor mit dem Mittelpunktswinkel $φ = 60 ^\circ$ ausgeschnitten, d.h. der Radius seiner Schultüte beträgt:
  $\displaystyle r=\dfrac{R \cdot 60^\circ}{360^\circ}= \dfrac {R}{6}$
  Da $R=50 \mathrm{cm}$ ist, beträgt sein Kegelradius: $r = \dfrac {50}{6}\mathrm{cm}$ .
  In der Abbildung des Kegels gilt für das eingezeichnete rechtwinklige Dreieck der Satz des Pythagoras:
  $r^2+h^2=R^2 \;\; \mathrm{(III)}$
  $h= \sqrt{R^2-r^2} \;\;\;\mathrm{(IV)}$
  Mit $R= 50 \mathrm{cm}$ und $r = \dfrac {50}{6}\mathrm{cm}$ erhält man für die Höhe $h$ :
  $h= \sqrt{50^2-(\dfrac{50}{6})^2}$
  $h= \dfrac{50}{6} \cdot \sqrt{35} \mathrm{cm}$
  Setzt man $r$ und $h$ in Gleichung $\mathrm{(I)}$ ein, ergibt sich ein Volumen von:
  $V= \dfrac{1}{3}\pi\cdot (\dfrac{50}{6})^2\cdot \dfrac{50}{6} \cdot \sqrt{35} \approx 3585{,}25 \mathrm{cm^3}$
  Volumen von Janas Schultüte
  Jana hat einen Kreissektor mit dem Mittelpunktswinkel $φ = 120 ^\circ$ ausgeschnitten, d.h. der Radius ihrer Schultüte beträgt:
  $r=\dfrac{R \cdot 120^\circ}{360^\circ}= \dfrac {R}{3}$
  Da $R= 50 \mathrm{cm}$ ist, beträgt ihr Kegelradius :
  $\displaystyle r = \dfrac {50}{3}\mathrm{cm}$
  Für die Höhe $h$ erhält man gemäß Gleichung $\mathrm{(IV)}$ :
  $\displaystyle h= \sqrt{50^2-(\dfrac{50}{3})^2}$
  $\displaystyle h= \dfrac{50}{3} \cdot \sqrt{8} \mathrm{cm}$
  Setzt man $r$ und $h$ in Gleichung $\mathrm{(I)}$ ein, ergibt sich ein Volumen von:
  $V= \dfrac{1}{3}\pi\cdot (\dfrac{50}{3})^2\cdot \dfrac{50}{3} \cdot \sqrt{8} \approx 13712{,}60 \mathrm{cm^3}$
  Antwort
  Jana liegt falsch. Ihr Kegelvolumen ist rund viermal so groß wie das Kegelvolumen von Nish.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Lina kommt später zum Basteln dazu und bekommt die Diskussion zwischen Nish und Jana mit. Sie möchte beide übertrumpfen und eine Schultüte basteln, in die am meisten Süßes rein passt. Sie benutzt ein übriges rundes Papier mit $R=50\;\text{cm}$ und schneidet einen Kreissektor mit Mittelpunktswinkel $\varphi$ aus dem Papier aus. Bestimme den Winkel $\varphi$ , für den das Kegelvolumen maximal wird.
  
  Teillösung b)
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwert
  Aufstellen der Zielfunktion und der Nebenbedingung
  Die Zielfunktion bei dieser Aufgabe ist das Volumen eines Kegels:
  $\displaystyle V= \dfrac{1}{3}\pi\cdot r^2\cdot h \;\;\; \mathrm{(I)}$
  Die Nebenbedingung ergibt sich aus der obigen rechten Abbildung.
  Im rechtwinkligen Dreieck gilt der Satz des Pythagoras:
  $\displaystyle r^2+h^2=R^2 \;\;\; \mathrm{(III)}$
  Einsetzen in die Zielfunktion
  Die einfachste Lösung der Extremwertaufgabe erhält man, wenn Gleichung $\mathrm{(III)}$ nach $r^{2}$ aufgelöst und in Gleichung $\mathrm{(I)}$ eingesetzt wird. Mit $R= 50 \mathrm{cm}$ folgt:
  $\displaystyle r^2 = 50^2-h^2\\\Rightarrow V(h) = \dfrac{1}{3}\pi\cdot (50^2-h^2)\cdot h$
  $\displaystyle V(h) = \dfrac{1}{3}\pi\cdot (2500 \cdot h-h^3) \;\;\;\;\;\;\; \mathrm{(V)}$
  Für den Definitionsbereich $\mathbb{D}$ gilt: $0\lt h\lt 50$ .
  Anmerkung: Für $h = 0$ und $h = 50$ ist das Volumen gleich Null.
  Bestimmung des Extremwertes
  Leite die Extremalfunktion $\mathrm{(V)}$ zweimal ab, um den Extremwert und die Art des Extremwertes bestimmen zu können.
  $\displaystyle V'(h)=\dfrac{1}{3}\pi\cdot (2500-3h^2)$
  $\displaystyle V''(h) = \dfrac{1}{3}\pi\cdot (-6h)= -2\pi h<0$
  Setze die erste Ableitung gleich Null:
  $\displaystyle 0=\dfrac{1}{3}\pi\cdot (2500-3h^2)\Rightarrow 2500=3h^2$
  Nach $h$ aufgelöst erhält man :
  $\displaystyle h=\sqrt{\dfrac{2500}{3}} \approx 28{,}87 \mathrm{cm} \;\;\;\; \mathrm{(VI)}$
  Da $0 \lt h \lt 50$ ist, gilt: $h \in \mathbb{D}$ .
  Setze Gleichung $\mathrm{(VI)}$ in die zweite Ableitung ein:
  $\displaystyle V''(\sqrt{\dfrac{2500}{3}}) = -2\pi\cdot \sqrt{\dfrac{2500}{3}}<0$
  Da die zweite Ableitung kleiner Null ist, ist der Extremwert ein Maximum.
  Bestimmung des Kegelgrundkreisradius
  Setzt man Gleichung $\mathrm{(VI)}$ $h=\sqrt{\dfrac{2500}{3}}$ in $r^{2} = 50^{2} - h^{2}$ ein,
  so erhält man:
  $\displaystyle r^2 = 2500-\dfrac{2500}{3}= \dfrac{5000}{3}$
  Zieht man die Wurzel aus $r^{2}$ , so erhält man für den Radius $r$ des Grundkreises des Kegels : $r= \sqrt{\dfrac{5000}{3}}\approx 40{,}82 \mathrm{cm} \;\;\;\; \mathrm{(VII)}$
  Bestimmung des Mittelpunktswinkels
  Löse Gleichung $\mathrm{(II)}$ nach $\varphi$ auf:
  $\displaystyle \varphi = \dfrac{r \cdot 360^\circ}{R}$
  Mit $R=50\mathrm{cm}$ und $r= \sqrt{\dfrac{5000}{3}} \mathrm{cm}$ folgt für $\varphi$ : $\varphi =\dfrac{\sqrt{\dfrac{5000}{3}}\cdot 360^\circ}{50}\approx 293{,}94^ \circ$
  Das maximale Volumen
  Setzt man die Gleichungen $\mathrm{(VI)}$ und $\mathrm{(VII)}$ in Gleichung $\mathrm{(I)}$ ein, so erhält man das maximale Volumen
  für einen Radius von $R= 50 \mathrm{cm}$ :
  $V_{max}=\dfrac{1}{3}\cdot\pi\cdot \dfrac{5000}{3}\cdot \sqrt{\dfrac{2500}{3}} \approx 50383{,}32 \mathrm{cm^3}$
  Antwort
  Das maximale Volumen $V_{max}$ der Schultüte beträgt in etwa $50383{,}32 \mathrm{cm^3}$ bei einem Radius des Grundkreises des Kegels von $r= \sqrt{\dfrac{5000}{3}}\approx 40{,}82 \mathrm{cm}$ und einer Kegelhöhe von
  $h=\sqrt{\dfrac{2500}{3}} \approx 28{,}87 \mathrm{cm}$ . Der Mittelpunktswinkel muss dafür $\varphi \approx 293{,}94^\circ$ betragen.
  Lina muss also einen Kreissektor mit dem Mittelpunktswinkel $\varphi \approx 293{,}94^\circ$ herausschneiden, um die größte Schultüte zu basteln.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Beurteile an Hand von Durchmesser und Höhe des Kegels, ob sich die gebastelten Kegelmäntel auch als Schultüten eignen.
  
  Teillösung c)
  Die Schultüten von Jana, Nish und Lina haben folgende Maße:
  Name
  Höhe
  Kreisdurchmesser
  Nish
  49,3 cm
  16,7 cm
  Jana
  47,1 cm
  33,3 cm
  Lina
  29 cm
  82 cm
  Bei üblichen Schultüten findet man Verhältnisse von Durchmesser zu Höhe von $1 : 2; 1 : 3$ bis $1 : 4$ .
  Betrachtet man die gebastelten Schultüten, so hat die Tüte von Nish ein Verhältnis von Durchmesser zu Höhe von etwa $1 : 3$ , d.h. seine Tüte passt am besten zu den obigen Verhältnissen. Janas Tüte hat ein Verhältnis von $1 : 1,5$ d.h. ihre Tüte ist etwas zu breit im Vergleich zur Höhe.
  Linas Tüte hat ein Verhältnis von Durchmesser zu Höhe von etwa $2,8 : 1$ . Ihre Tüte ist sehr breit im Vergleich zur Höhe. Dadurch lässt sich die Schultüte schwer in der Hand halten. Lina könnte dadurch wertvolle Süßigkeiten verlieren. Daher findet man beim Kauf eher längliche Schultüten.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Name	Höhe	Kreisdurchmesser
Nish	49,3 cm	16,7 cm
Jana	47,1 cm	33,3 cm
Lina	29 cm	82 cm

Ein Bauer will eine neue Weide in Form eines Rechtecks anlegen. Die eine Seite grenzt aber bereits an die $30\m$ lange Scheune an. Der Bauer hat $90\m$ Zaun zur Verfügung und möchte eine Fläche mit dem größtmöglichen Flächeninhalt einzäunen.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle \dfrac{a}{b}$	$=$	$\displaystyle \dfrac{a-y}{x}$	$\displaystyle \left(Strahlensatz\ V-Figur\right)$
	↓	Löse nach $y$ auf.
$\displaystyle y$	$=$	$\displaystyle \dfrac{a}{b}\left(b-x\right)$
	↓	Setze in die Flächenfunktion ein.

Der Zaun reicht für drei Seiten des Rechtecks
	↓
$\displaystyle 2a+2b-30$	$=$	$\displaystyle 90$	$\displaystyle +30$
	↓	Nach b umformen
$\displaystyle 2a+2b$	$=$	$\displaystyle 120$	$\displaystyle -2a$
$\displaystyle 2b$	$=$	$\displaystyle 120-2a$	$\displaystyle :2$
$\displaystyle b$	$=$	$\displaystyle 60-a$

$\displaystyle A(a)$	$=$	$\displaystyle a\cdot(60-a)$
	$=$	$\displaystyle -a^2+60a$
	$=$	$\displaystyle a\left(60-a\right)$

$\displaystyle A$	$=$	$\displaystyle \dfrac{ab}{4}$
	↓	Setze die Werte ein und berechne die Fläche.
	$=$	$\displaystyle \dfrac{32m\cdot48m}{4}$
	$=$	$\displaystyle 384m^2$

Aufgaben zu Extremwertproblemen aus der Geometrie

Lösung

Quellen

Schultüten

Teillösung a)

Volumen von Nishs Schultüte

Volumen von Janas Schultüte

Antwort

Hast du eine Frage oder Feedback?

Teillösung b)

Aufstellen der Zielfunktion und der Nebenbedingung

Einsetzen in die Zielfunktion

Bestimmung des Extremwertes

Bestimmung des Kegelgrundkreisradius

Bestimmung des Mittelpunktswinkels

Das maximale Volumen

Antwort

Hast du eine Frage oder Feedback?

Teillösung c)

Hast du eine Frage oder Feedback?