Der Scheitelpunkt ist der höchste bzw. tiefste Punkt (Extrempunkt) einer Parabel.

Eigenschaften des Scheitelpunkts
Der Scheitelpunkt ist das Maximum der Funktion, wenn die Parabel nach unten geöffnet ist und Minimum der Funktion, wenn die Parabel nach oben geöffnet ist.
Die Parabel ist achsensymmetrisch zur Parallelen zur y-Achse durch den Scheitelpunkt.
Der Scheitelpunkt lautet und ist hier ein Minimum, da die Parabel nach oben geöffnet ist.
Die Parabel ist achsensymmetrisch zur Geraden .
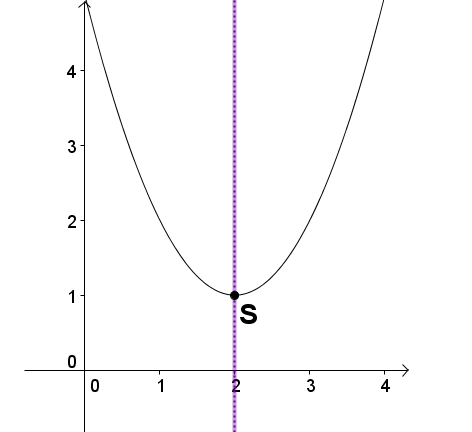
Scheitelpunkt
Bestimmung des Scheitelpunkts
Es gibt vier unterschiedliche Methoden zur Bestimmung des Scheitelpunktes:
anhand der Scheitelform
anhand der allgemeinen Form
mithilfe der Ableitung (fortgeschritten)
anhand der Nullstellen (nicht immer anwendbar)
1. Bestimmung anhand der Scheitelform
Wenn sich die Funktion schon in Scheitelform (Scheitelpunktform) befindet, kann der Punkt einfach abgelesen werden:
Scheitelpunktform:
Scheitelpunkt:
Achte auf die unterschiedlichen Vorzeichen der Funktionen!
Aus der Funktion lässt sich und ablesen. Der Scheitelpunkt befindet sich folglich am Punkt .
Ist die Funktion , folgt und . Somit ist der Scheitelpunkt bei .
Ist die Funktion , folgt und . Somit ist der Scheitelpunkt bei .
Umwandlung in Scheitelform
Falls die Gleichung noch nicht in Scheitelform ist, kann man sie mit der quadratischen Ergänzung oder anderen Umformungen (Ausmultiplizieren, Ausklammern, binomische Formel) in Scheitelform bringen und dann, wie oben bereits erklärt, den Scheitelpunkt ablesen.
2. Bestimmung anhand der allgemeinen Form
Mithilfe der folgenden Formel kann man den Scheitelpunkt auch direkt aus der allgemeinen Form berechnen.
Allgemeine Form:
Es soll nun der Scheitelpunkt der Funktion anhand der Formel bestimmt werden.
Bestimme , , aus der allgemeinen Form.
Setze , , in die Formel ein.
Fasse die Terme zusammen, indem du Brüche kürzt und subtrahierst.
Umwandeln in die allgemeine Form
Falls die Gleichung noch nicht in der allgemeinen Form ist, kann man sie durch Umformungen wie Ausmultiplizieren, Ausklammern, binomische Formel in die allgemeine Form bringen und dann, wie oben bereits erklärt, den Scheitelpunkt durch die Formel berechnen.
3. Bestimmung mit der Ableitung (fortgeschritten)
Die Steigung der Parabel ist am Scheitelpunkt gleich . Deshalb kann der Scheitel einer Parabel auch mit der Ableitung berechnet werden, da der Scheitel stets das Extremum der quadratischen Funktion ist.
Es soll der Scheitelpunkt von mittels der Methode Bestimmung mit der Ableitung berechnet werden.
Leite die Funktion ab.
Bestimme für die Extremstelle die Nullstelle der ersten Ableitung, das bedeutet .
| ↓ | Setze ein und löse nach auf. | ||
Dies ist die Extremstelle. Wir haben hier eine nach oben geöffnete Parabel, daher ist die Minimalstelle. Berechne den zugehörigen -Wert, indem du in die Funktion einsetzt.
Schreibe den Scheitelpunkt hin.
4. Bestimmung anhand der Nullstellen
Vorsicht! Diese Methode funktioniert nur, falls die Parabel Nullstellen hat.
Wenn die Parabel zwei Nullstellen hat, so liegt der Scheitel genau in der Mitte zwischen diesen beiden Nullstellen, da alle Parabeln achsensymmetrisch sind.
Wenn die Parabel nur eine Nullstelle hat, dann ist diese der x-Wert des Scheitels.
Wenn die Parabel keine Nullstellen hat, funktioniert diese Methode NICHT!
Berechne die Nullstellen von .
| ↓ | Ziehe die Wurzel. | ||
und
Die Nullstellen von sind und . Der -Wert des Scheitels liegt in der Mitte zwischen diesen beiden Nullstellen. Die Zahl liegt zwischen und .

Nullstellen von (schwarz) und -Wert des Scheitels mittig (rot)
Also ist .
Bestimme nun den -Wert des Scheitels , indem du den -Wert in die Funktionsgleichung von einsetzt.
| ↓ | Setze ein. | ||
| ↓ | Setze in ein. | ||
Der Scheitelpunkt von ist .
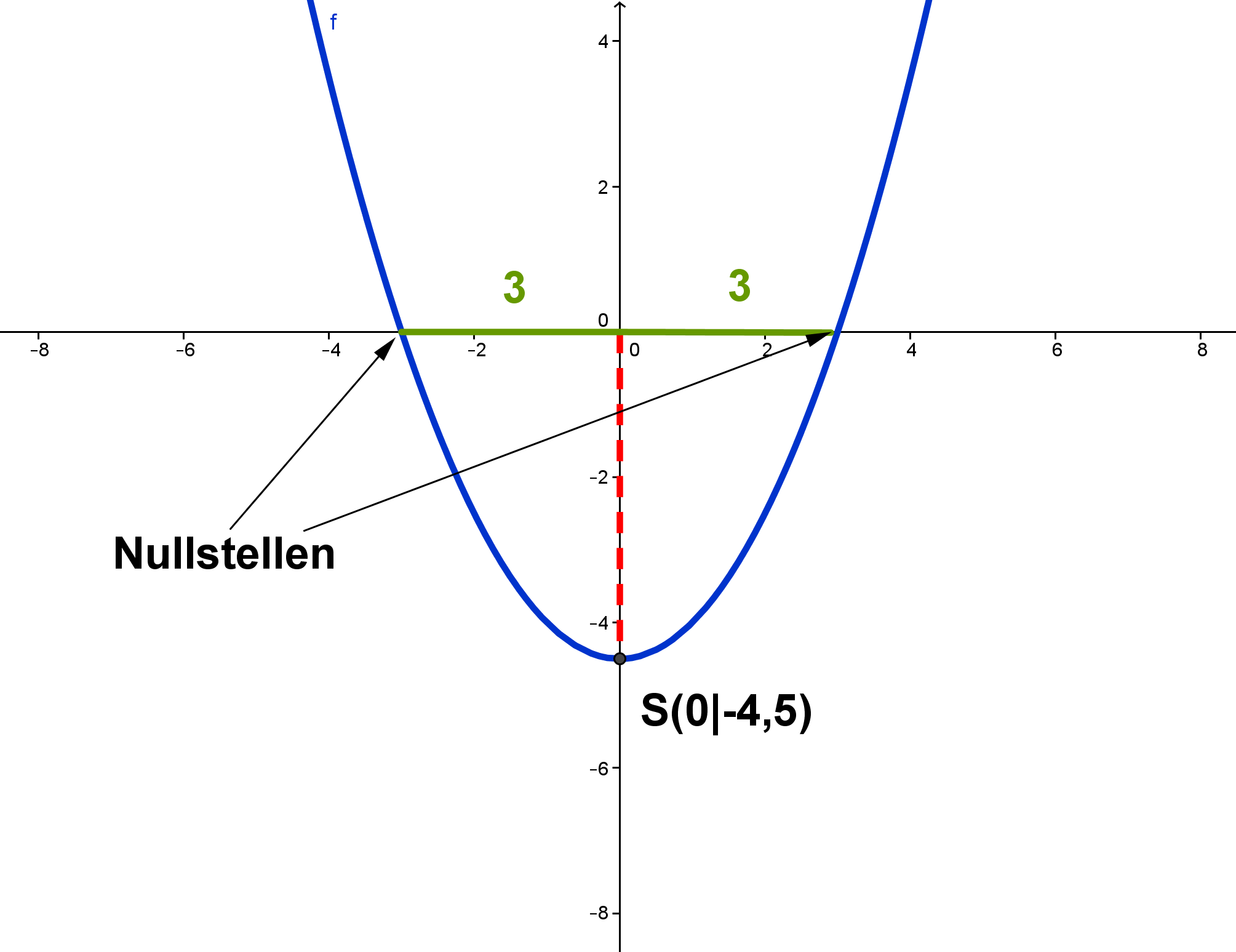
Graph der Funktion
Video zur Bestimmung des Scheitelpunkts anhand der Nullstellen
Laden
Übungsaufgaben
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zur Berechnung des Scheitelpunktes
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
