Eine Parabel ist der Graph einer quadratischen Funktion. Parabeln haben ein typisches bogenförmiges Aussehen und können nach oben oder nach unten geöffnet sein. Ihr eindeutig bestimmter tiefster bzw. höchster Punkt heißt Scheitelpunkt.
Eine Parabel heißt Normalparabel, wenn ihre Funktionsgleichung lautet.
Normalparabel
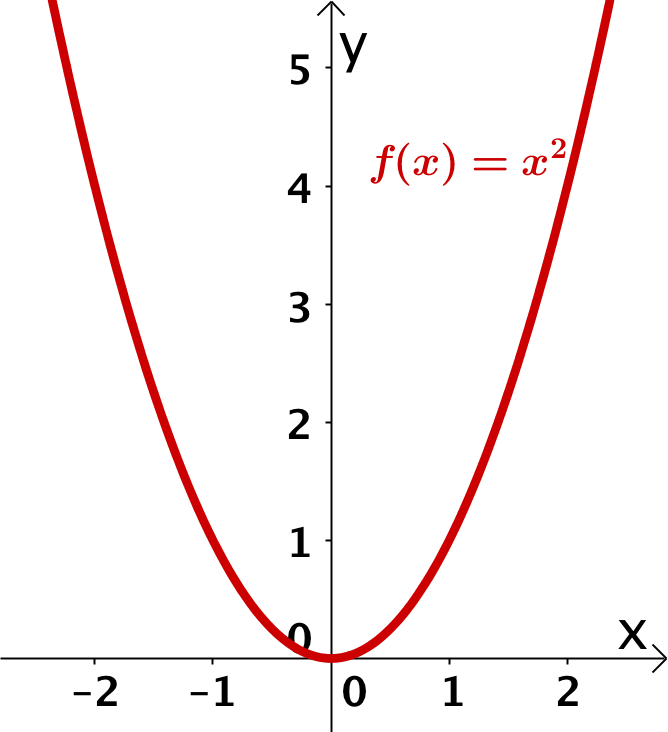
Die Normalparabel ist der Funktionsgraph der Funktion
Sie hat folgende Eigenschaften:
Scheitelpunkt bei
nach oben geöffnet
achsensymmetrisch zur -Achse
geht durch die Punkte
Allgemeine Parabel
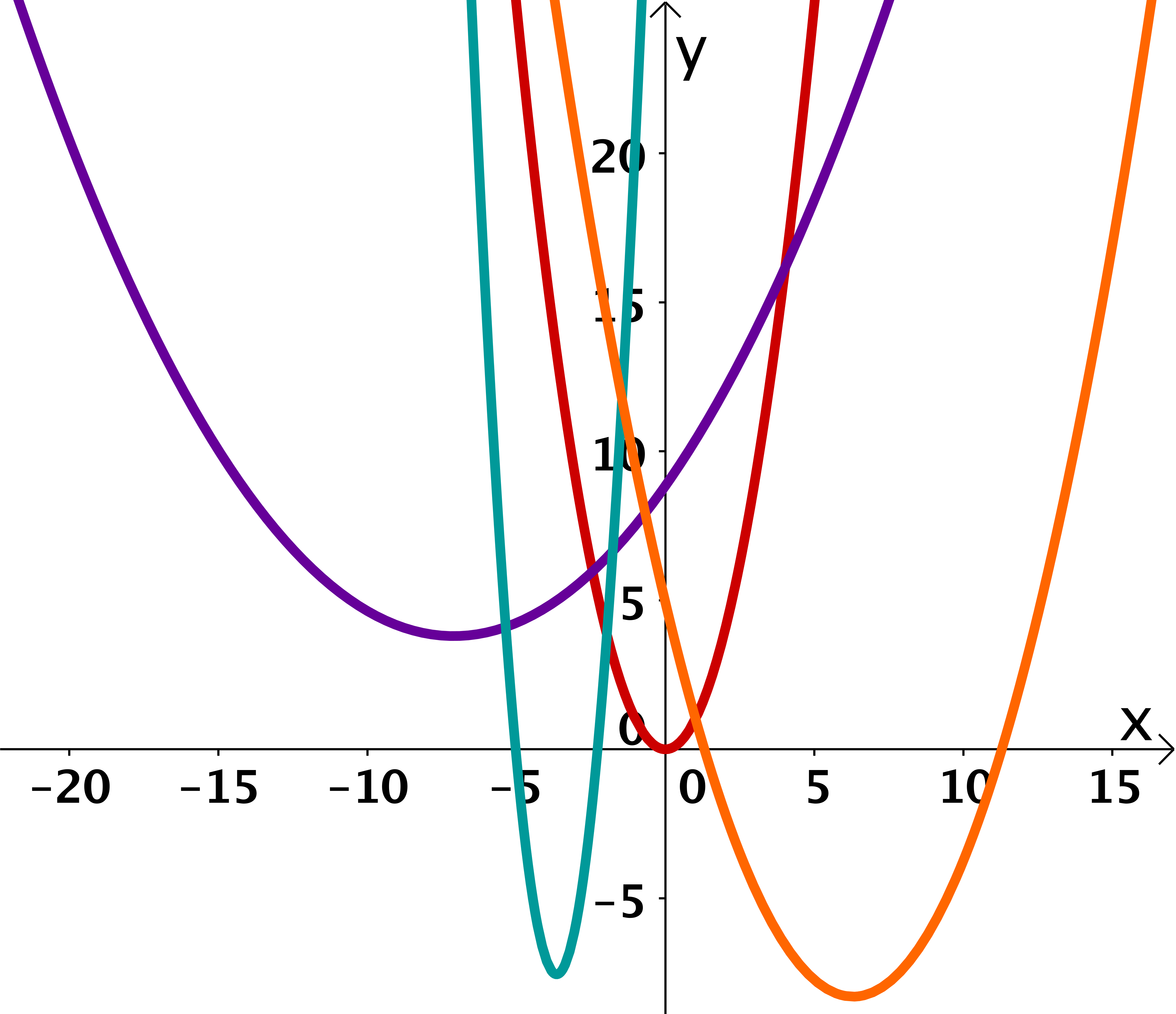
Ausgehend von der Normalparabel kann man jede beliebige Parabel konstruieren. Dazu benutzt man die Scheitelform:
Den Zusammenhang zwischen den Parametern in der Scheitelform und dem Graphen findest du in dem zugehörigen Artikel. Dadurch lassen sich verschiedenste Parabeln konstruieren, wie auch in dem Graphen rechts erkennbar ist.
Video zur Scheitelform
Laden
Parabel in Koordinatensystem zeichnen
Man kann Parabeln mithilfe einer Wertetabelle zeichnen oder mithilfe einer Parabelschablone und den Verformungsregeln.
Alternative Definition einer Parabel
Eine Parabel besteht aus denjenigen Punkten, die von einer vorgegebenen Gerade und einem vorgegebenen Punkt (Brennpunkt) gleich weit entfernt sind.
Veranschaulichung am Applet
Parabeln im Alltag
Parabeln findet man oft im Alltag wieder:
Wasserstrahlen, wie z.B. bei Trinkbrunnen, beschreiben Parabeln.
Wirft man einen Ball horizontal, so bekommt man eine Wurfparabel.
Bei Parabelflügen verläuft die Flugbahn des Flugzeugs längs einer Parabel. Parabelflüge werden benutzt, um unterschiedliche Schwerkraftsituationen zu simulieren.
Der Name Parabolantenne leitet sich vom parabelförmigen Querschnitt ab. (Parabeln nennt man allgemein Linien, die einen Brennpunkt haben, was hier genutzt wird, um Strahlen wie etwa bei den Satellitenschüsseln zu bündeln und damit zu verstärken.)
Auch unter Brücken findet man häufig Parabelbögen, da diese im Vergleich z.B. zu Kreisbögen stabiler sind.
Hingegen bilden Stromleitungen, die zwischen zwei Masten hängen, keine Parabel, sondern eine sogenannte Kettenlinie, die der Parabel nur sehr ähnlich sieht.

Übungsaufgaben
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zum Zeichnen und Vergleichen von Graphen
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
Artikel
- Einfluss der Parameter in der Scheitelform
- Scheitelpunkt einer Parabel
- Parabel zeichnen
- Quadratische Funktion
- Allgemeine Form und Scheitelform einer quadratischen Funktion