Einfluss der Parameter in der Scheitelform

Ausgehend von der Normalparabel kann man jede beliebige Parabel konstruieren. Dazu benutzt man die Scheitelform:

$f\left(x\right)=a(x-d)^2+e$

an der man den Scheitelpunkt $S(d|e)$ ablesen kann.

Folgenden Einfluss haben die einzelnen Parameter $a,d,e$ der Scheitelform auf den Graphen der Parabel:

Paramter	Einfluss auf	Graph
a	Öffnungsrichtung und Streckung/Stauchung $a>0$ : Parabel nach oben geöffnet $a<0$ : Parabel nach unten geöffnet $\|a\|<1$ : Parabel Richtung y-Achse gestaucht (im Vergleich zur Normalparabel) $\|a\|>1$ : Parabel Richtung y-Achse gestreckt (im Vergleich zur Normalparabel)
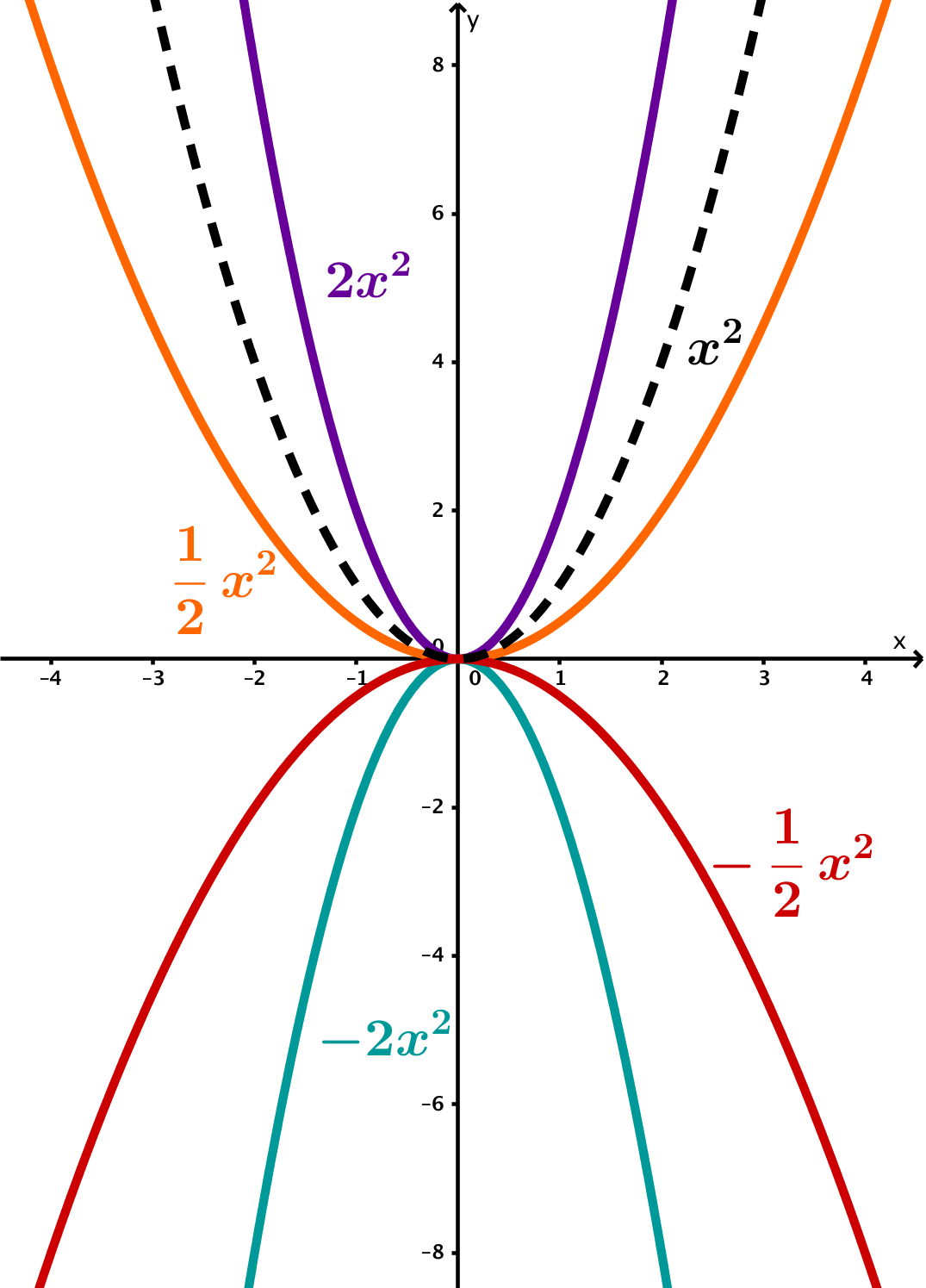d	Verschiebung in $x$ -Richtung $d>0$ : Verschiebung um $d$ nach rechts $d<0$ : Verschiebung um $d$ nach links
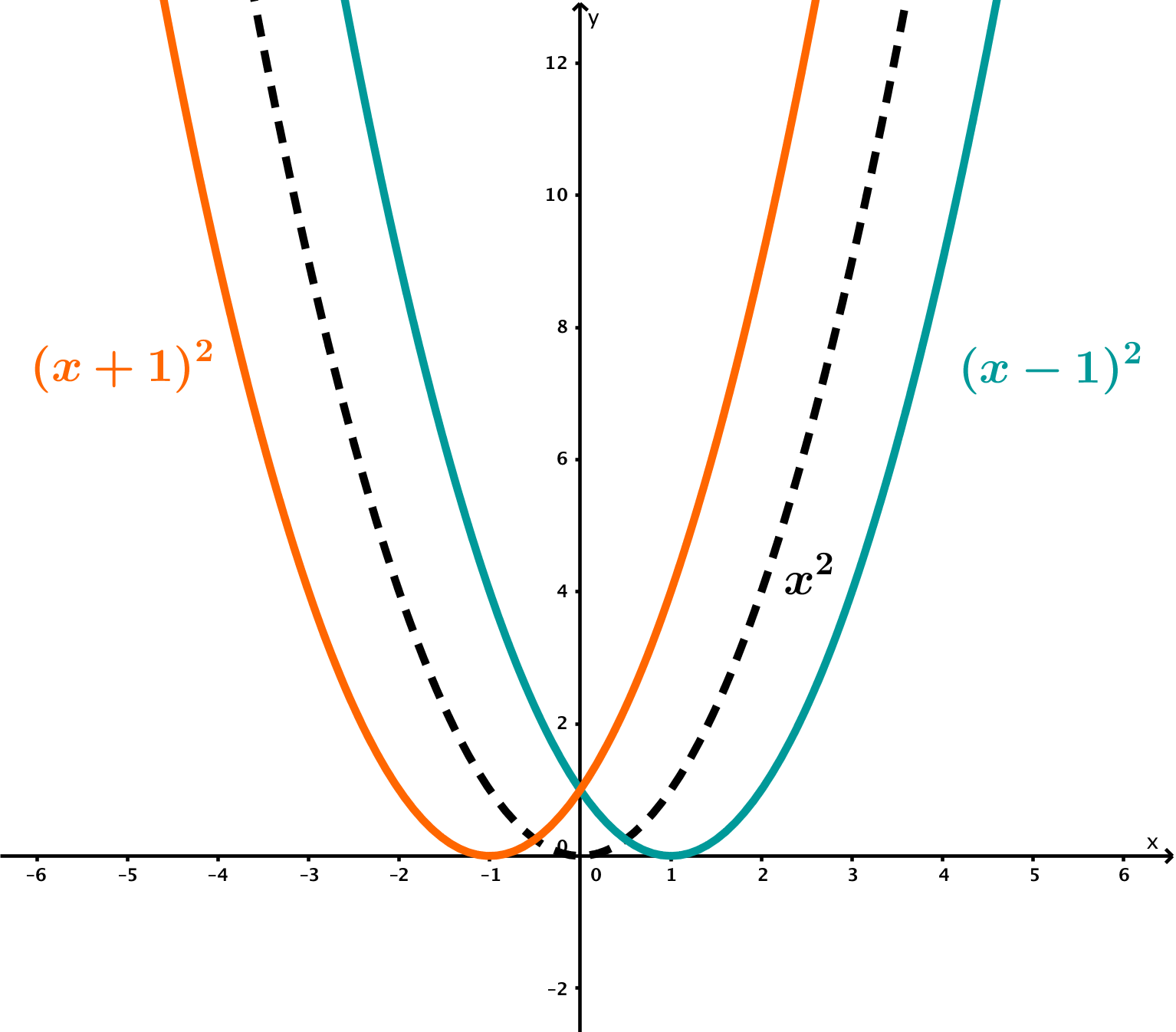e	Verschiebung in $y$ -Richtung $e>0$ : Verschiebung um $e$ nach oben $e<0$ : Verschiebung um $e$ nach unten

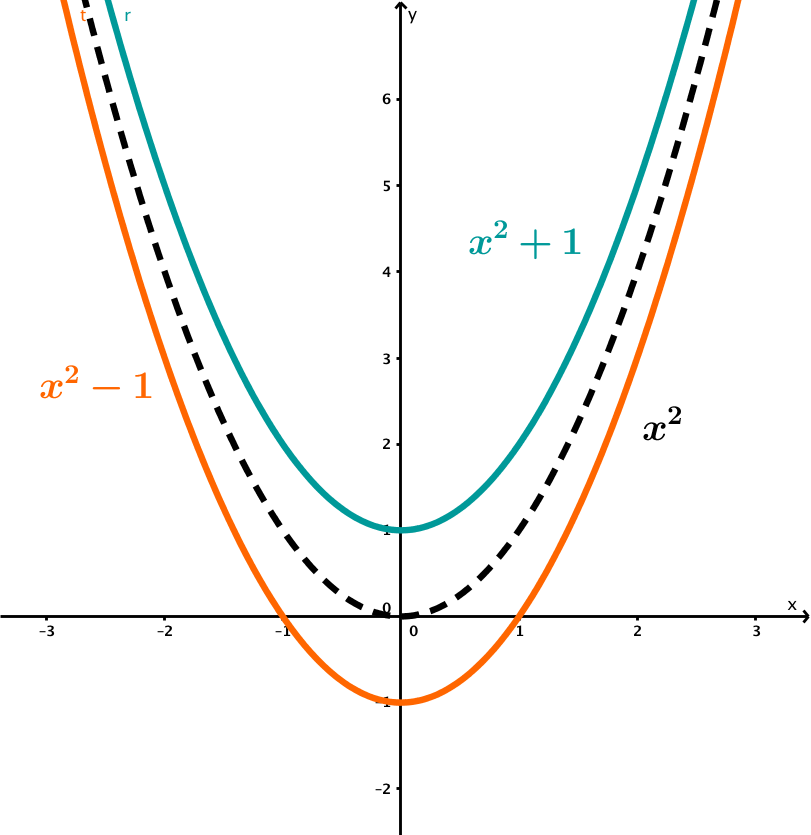Beispiel

Finde zu der nebenstehenden Parabel in dem Koordinatensystem die zugehörige Funktionsgleichung, das heißt mit passenden Parametern $a,d,e$ . Betrachte in der obigen Tabelle nochmal, welche Auswirkungen die Parameter haben.

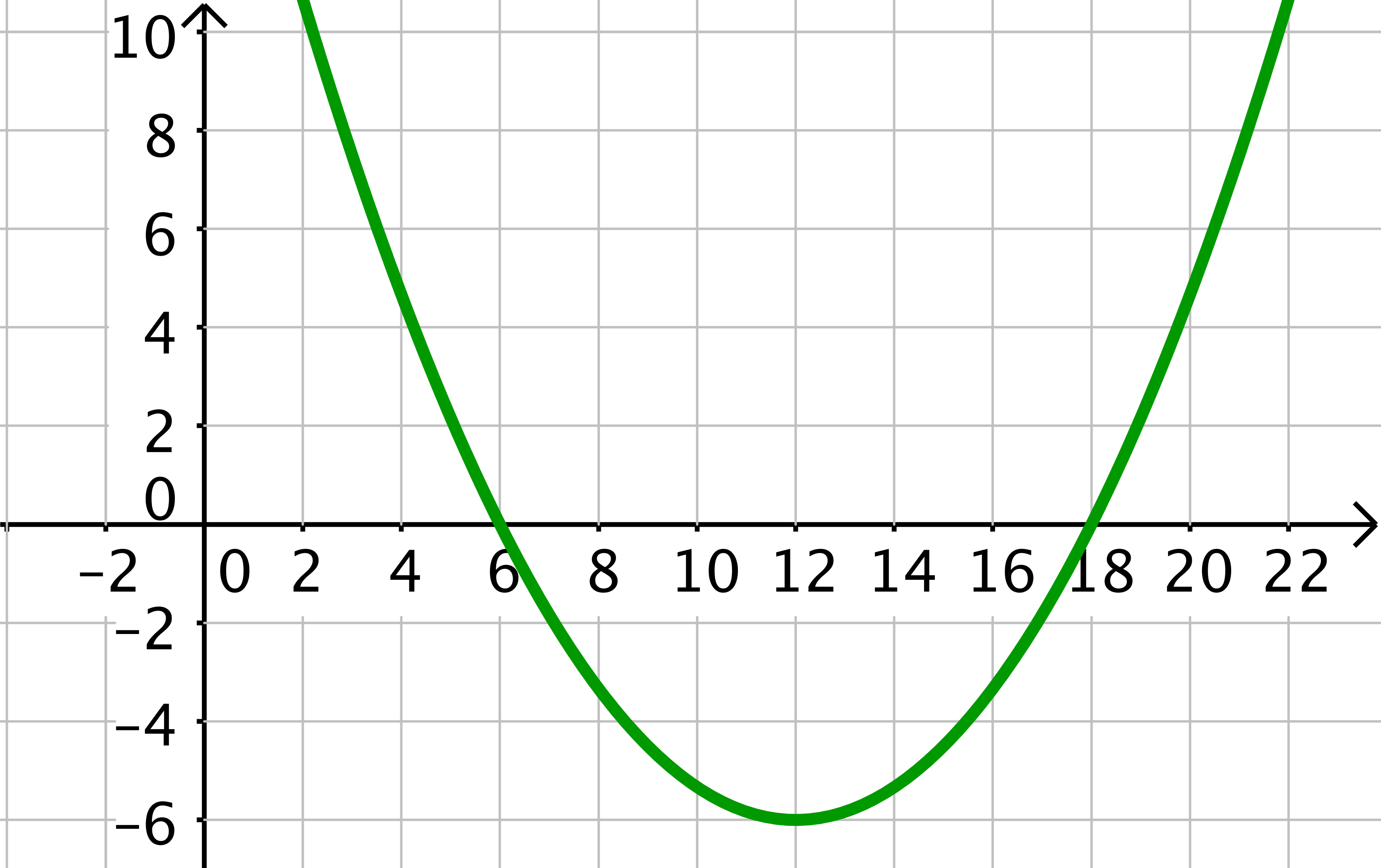
Im Graphen erkennst du den Scheitelpunkt der Parabel.

$S(12|-6)$

Verwende, dass in der Scheitelform $f(x)=a \cdot (x-d)^2+e$ der Scheitelpunkt $S(d|e)$ steckt.

$f(x)=a \cdot (x-12)^2-6$

Es bleibt noch der Parameter $a$ zu bestimmen. Hierzu kannst du einen Punkt vom Graphen ablesen und in die Funktionsgleichung einsetzen.

$(6|0)$ ist ein Punkt des Graphen von $f$

$0=f(6)$
	↓
$\displaystyle 0$	$=$	$\displaystyle a\cdot(6-12)^2-6$	$\displaystyle +6$
$\displaystyle 6$	$=$	$\displaystyle a(-6)^2$
$\displaystyle 6$	$=$	$\displaystyle a\cdot36$	$\displaystyle :36$
$\displaystyle a$	$=$	$\displaystyle \frac{1}{6}$

$f(x)=\frac{1}{6} (x-12)^2 -6$

Veranschaulichung durch ein Applet

Benutze die Schieberegler, um die Parameter zu verändern.

Mit einem Klick auf Bild oder Button oben stimmst du zu, dass externe Inhalte von GeoGebra geladen werden. Dabei können persönliche Daten zu diesem Service übertragen werden – entsprechend unserer Datenschutzerklärung.

[https://www.geogebra.org/material/iframe/id/MPwQbX2F]

Video zur Scheitelform

Laden

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?