Symmetrie von Graphen

Graphen können achsensymmetrisch oder punktsymmetrisch sein.

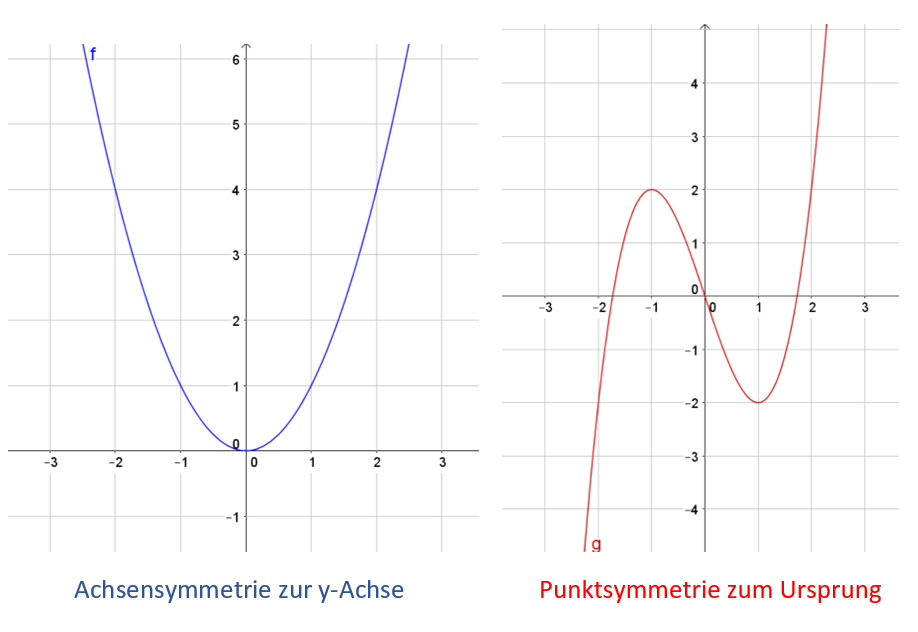
Bei einer Achsensymmetrie zur y-Achse gilt:

\displaystyle f(-x)=f(x)

Man sagt auch: die Funktion f ist gerade.

Bei Punktsymmetrie zum Ursprung gilt:

\displaystyle f(-x)=f(x)

Man sagt auch: die Funktion f ist ungerade.

Bestimmung der Symmetrie

Mit folgenden Schritten kannst du herausfinden, ob der Graph einer gegebenen Funktion $f$

achsensymmetrisch zur $y$ -Achse oder
punktsymmetrisch zum Ursprung ist

Vorgehen

Setze für $x$ in die Funktion $-x$ ein: $f(-x)$
Forme $f(-x)$ um, indem du alle Klammern, in denen $-x$ steht, umformst
Vergleiche diese Funktion $f(-x)$ mit der ursprünglichen Funktion $f(x)$ .

Folgende Fälle können eintreten:

Fall	Folgerung
$f(-x)=f(x)$	Der Graph von $f$ ist achsensymmetrisch zur $y$ -Achse.
$f(-x)=-f(x)$	Der Graph von $f$ ist punktsymmetrisch zum Ursprung.
$f(-x)$ ist weder $f(x)$ noch $-f(x)$	Der Graph von $f$ ist nicht achsensymmetrisch zur y-Achse und nicht punktsymmetrisch zum Ursprung.

Beispiele

Beispiel 1)

Gegeben ist die Funktion $f(x)=\frac{1}{1+x^2}$ . Wir wollen untersuchen, ob der Graph von $f$ achsensymmetrisch zur $y$ -Achse oder punktsymmetrisch zum Ursprung ist. Dafür setzen wir in $f(x)$ den Wert $-x$ ein:

Setze in $f(x)=\frac{1}{1+x^2}$ statt $x$ den Wert $-x$ ein.
	↓
$\displaystyle f(-x)$	$=$	$\displaystyle \frac{1}{1+(-x)^2}$
	↓	Vereinfache.
	$=$	$\displaystyle \frac{1}{1+\left(-1\cdot x\right)^2}$
	$=$	$\displaystyle \frac{1}{1+\left(-1\right)^2\cdot x^2}$
	↓	$(-1)^2 =1$
	$=$	$\displaystyle \frac{1}{1+x^2}$
	$=$	$\displaystyle f(x)$

$\Rightarrow f(-x)=f(x)$ und somit: Der Graph von $f(x)=\frac1{1+x^2}$ ist achsensymmetrisch zur $y$ -Achse.

Dass die Rechnung stimmt, sieht man auch, wenn man den Graphen von $f$ ansieht.

Beispiel 2)

Gegeben ist die Funktion $g(x)=\frac{x}{1+x^2}$ . Wir untersuchen, ob der Graph von $g$ achsensymmetrisch zur $y$ -Achse oder punktsymmetrisch zum Ursprung ist. Dafür setzen wir in $g(x)$ den Wert $-x$ ein.

Setze in $g(x)=\frac{x}{1+x^2}$ statt $x$ den Wert $-x$ ein.
	↓
$\displaystyle g\left(-x\right)$	$=$	$\displaystyle \frac{-x}{1+\left(-x\right)^2}$
	↓	Vereinfache. $(-x)^2=x^2$
	$=$	$\displaystyle \frac{-x}{1+x^2}$
	↓	Ziehe das Minus im Zähler vor den Bruch. $-x=(-1)\cdot x$
	$=$	$\displaystyle -\left(\frac{x}{1+x^2}\right)$
	$=$	$\displaystyle -g\left(x\right)$

$\Rightarrow g(-x)=-g(x)$ und somit: Der Graph von $g(x)=\frac x {1+x^2}$ ist punktsymmetrisch zum Ursprung.

Zeichnet man den Graphen von $g$ , sieht man die Punktsymmetrie zum Ursprung.

Beispiel 3)

Gegeben ist die Funktion $h\left(x\right)=\frac{x}{1+x^2}+2$ . Wir untersuchen, ob der Graph von $h$ achsensymmetrisch zur $y$ -Achse oder punktsymmetrisch zum Ursprung ist. Dafür setzen wir in $h(x)$ den Wert $-x$ ein.

Setze in $h(x)=\frac{x}{1+x^2}+2$ statt $x$ den Wert $-x$ ein.
	↓
$\displaystyle h\left(-x\right)$	$=$	$\displaystyle \frac{-x}{1+\left(-x\right)^2}+2$
	↓	Vereinfache. $(-x)^2=x^2$
	$=$	$\displaystyle \frac{-x}{1+x^2}+2$
	↓	Ziehe das Minus im Zähler vor den Bruch. $-x=(-1)\cdot x$
	$=$	$\displaystyle -\left(\frac{x}{1+x^2}\right)+2$

$h(-x)$ ist also weder $h\left(x\right)=\frac{x}{1+x^2}+2$ noch $-h\left(x\right)=-\left(\frac{x}{1+x^2}+2\right)=-\frac{x}{1+x^2}-2$ und somit weder achsensymmetrisch zur y-Achse noch punktsymmetrisch zum Ursprung.

Bemerkung: $h(x)$ ist zwar nicht punktsymmetrisch zum Ursprung, aber zu einem anderen Punkt - und zwar zum Punkt $P(0|2)$ .

Hilfreiche Regel für Polynomfunktionen

Auch bei Polynomen kannst du überprüfen, ob $f(-x)$ entweder $-f(x)$ oder $f(x)$ entspricht. Die folgenden Regeln zeigen dir, wie es schneller gehen kann:

Merke

Für ein vollständig ausmultipliziertes Polynom $f(x)=a_n\cdot x^n+a_{n-1}\cdot x^{n-1}+\dots+a_1\cdot x^1+a_0$ gilt:

alle Potenzen sind gerade (der konstante Term $a_0$ zählt ebenfalls als gerade Potenz) $\Rightarrow$ Achsensymmetrie zur y-Achse. Die Funktion f ist gerade.
alle Potenzen sind ungerade $\Rightarrow$ Punktsymmetrie zum Ursprung. Die Funktion f ist ungerade.

Beispiele

Das Polynom $f(x)=4x^6-3x^2+1$ ist achsensymmetrisch zur $y$ -Achse, da es nur die geraden Potenzen $6$ , $2$ sowie die $0$ (für die Konstante $+1$ ) enthält.
Das Polynom $g\left(x\right)=2x^3+x$ ist punktsymmetrisch zum Ursprung, da es nur die ungeraden Potenzen $3$ und $1$ enthält.
Das Polynom $h\left(x\right)=2x^4+3x^3+3$ ist weder achsensymmetrisch zur $y$ -Achse noch punktsymmetrisch zum Ursprung, da es sowohl gerade ( $4$ ), die Null sowie ungerade ( $3$ ) Potenzen enthält.

Video zur Symmetrie

Inhalt wird geladen…

Hilfreiche Regel für gebrochenrationale Funktionen

Auch bei gebrochenrationalen Funktionen kannst du überprüfen, ob $f(-x)$ entweder $-f(x)$ oder $f(x)$ entspricht. Die folgenden Regeln zeigen dir, wie es schneller gehen kann:

Merke

Betrachte die Zähler- und Nennerfunktion einer gebrochen-rationalen Funktion.

AS: Graph der Funktion ist achsensymmetrisch zur y-Achse.

PS: Graph der Funktion ist punktsymmetrisch zum Ursprung.

Achsensymmetrie

Der Graph einer gebrochenrationalen Funktion ist achsensymmetrisch zur $y$ -Achse , wenn die Zähler- und die Nennerfunktion die gleiche Symmetrie haben.

$f(x)=\frac{\color{green}{\mathrm{AS}}}{\color{green}{\mathrm{AS}}}\;\Rightarrow\;\color{green}{\mathrm{AS}}$
$f(x)=\frac{\color{660099}{\mathrm{PS}}}{\color{660099}{\mathrm{PS}}}\;\Rightarrow\;\color{green}{\mathrm{AS}}$

Punktsymmetrie

Der Graph einer gebrochenrationalen Funktion ist punktsymmetrisch zum Ursprung, wenn die Zähler- und Nennerfunktion unterschiedliche Symmetrien haben.

$f(x)=\frac{\color{green}{\mathrm{AS}}}{\color{660099}{\mathrm{PS}}}\;\Rightarrow\;\color{660099}{\mathrm{PS}}$
$f(x)=\frac{\color{660099}{\mathrm{PS}}}{\color{green}{\mathrm{AS}}}\;\Rightarrow\;\color{660099}{\mathrm{PS}}$

Beispiele

Beispiel 1)

Der Graph der Funktion $f(x)=\frac1{x^2-1}$ ist achsensymmetrisch zur $y$ -Achse, weil der Graph der Zählerfunktion $z(x)=1$ achsensymmetrisch zur $y$ -Achse ist und der Graph der Nennerfunktion $n(x)=x^2-1$ wegen $n(-x)=(-x)^2-1=x^2-1=n(x)$ achsensymmetrisch zur $y$ -Achse ist.

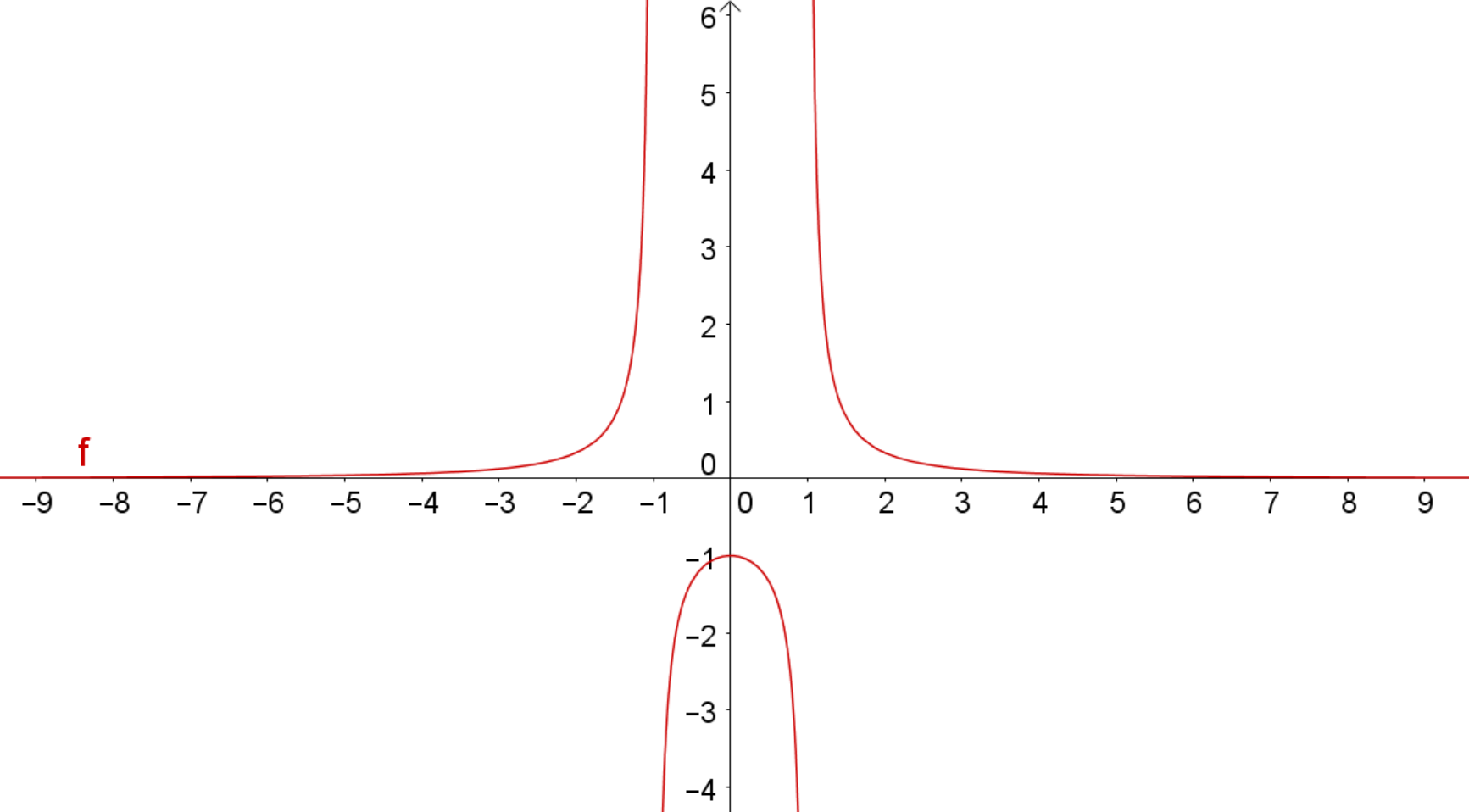
f geplottet. f ist achsensymmetrisch zur y-Achse

Beispiel 2)

Der Graph der Funktion $g(x)=\frac{x}{x^2-1}$ ist punktsymmetrisch zum Ursprung, weil der Graph der Zählerfunktion $z(x)=x$ wegen $z(-x)=-x=-z(x)$ punktsymmetrisch zum Ursprung ist und der Graph der Nennerfunktion $n(x)$ achsensymmetrisch zur $y$ -Achse ist.

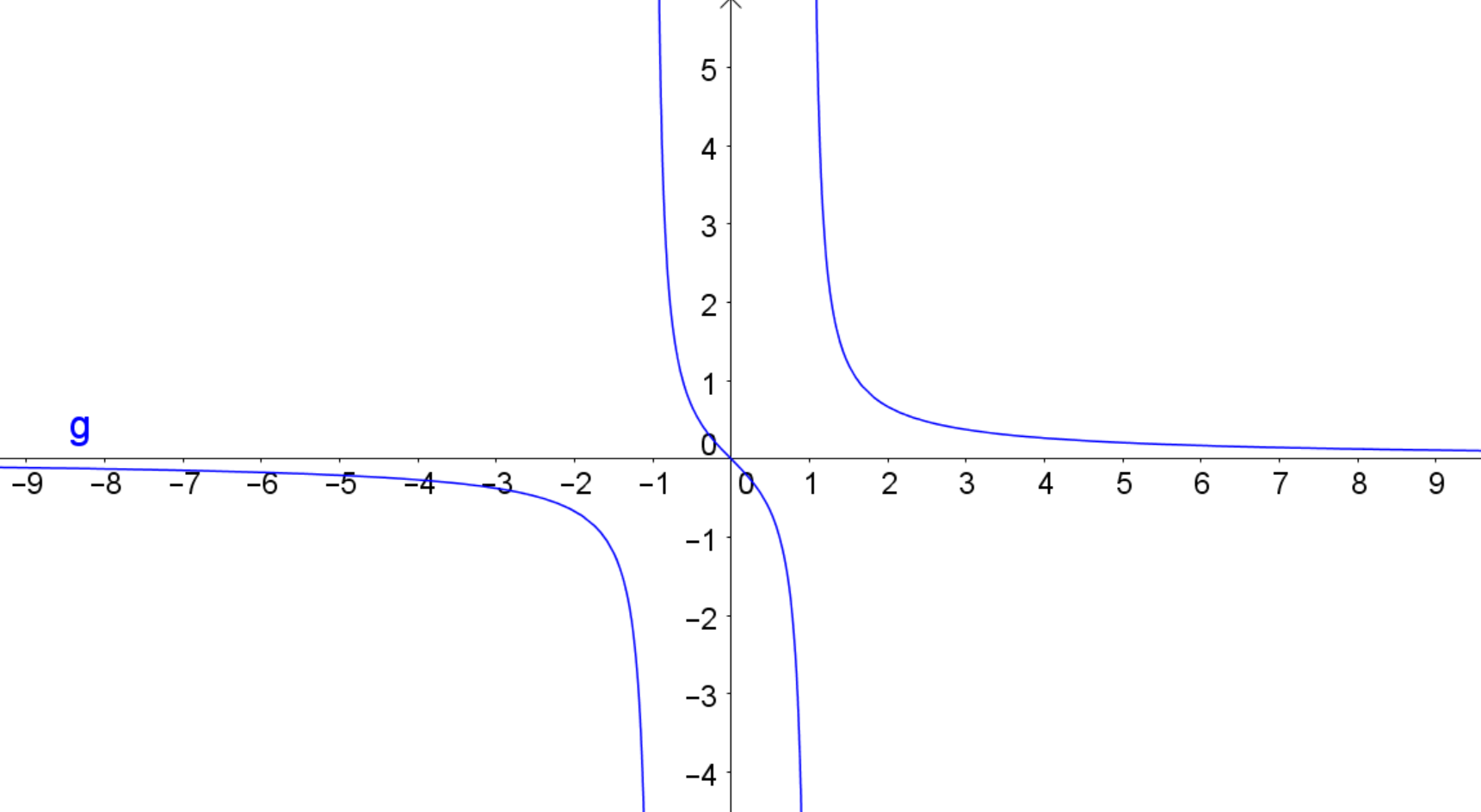
g geplottet. g ist punktsymmetrisch zum Ursprung

Beispiel 3)

Gegeben ist die Funktion $h(x)=\frac{x^2-x}{x^3-x}$ . Der Graph der Nennerfunktion $n(x)=x^3-x$ ist punktsymmetrisch zum Ursprung, weil diese Polynomfunktion nur ungerade Exponenten enthält. Der Graph der Polynom-Zählerfunktion $z(x)=x^2-x$ ist weder punktsymmetrisch zum Ursprung, noch achsensymmetrisch zur $y$ -Achse, weil sie sowohl gerade als auch ungerade Exponenten enthält. Deshalb ist auch der Graph der gesamten Funktion $h(x)$ weder achsensymmetrisch zur $y$ -Achse noch punktsymmetrisch zum Ursprung.

h geplottet. h ist weder achsensymmetrisch zur y-Achse, noch punktsymmetrisch zum Ursprung

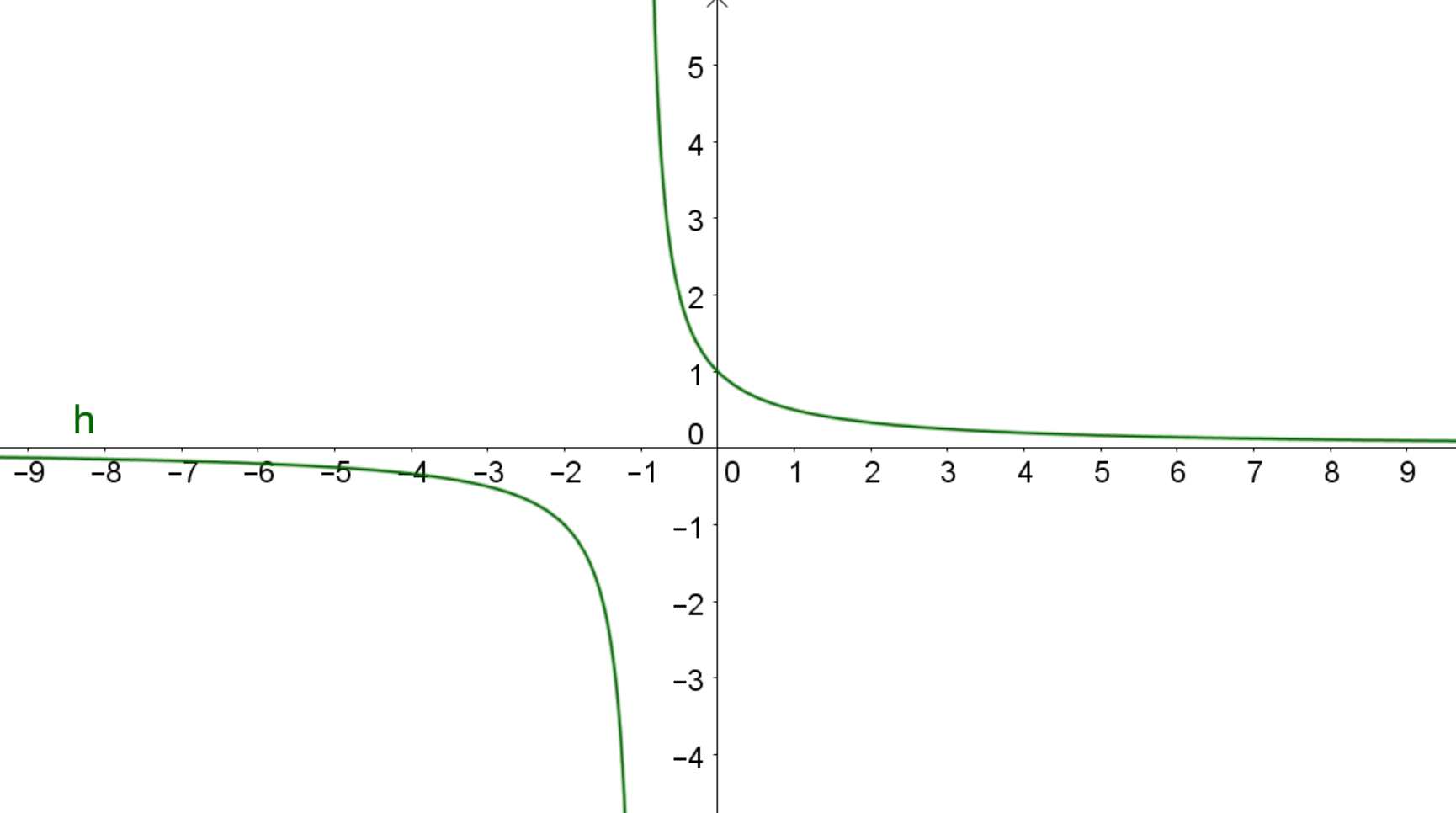
Symmetrie von Ableitungen und Stammfunktionen

Symmetrie von Ableitungen

Merke

Ist der Graph einer Funktion $f$ punktsymmetrisch zum Ursprung, dann ist der Graph der Ableitungsfunktion $f'$ achsensymmetrisch zur $y$ -Achse.
Ist der Graph einer Funktion $f$ achsensymmetrisch zur $y$ -Achse, dann ist der Graph der Ableitungsfunktion $f'$ punktsymmetrisch zum Ursprung.

Allgemein gilt:

Ist der Graph einer Funktion $f$ punktsymmetrisch zu einem Punkt $\left(a,b\right)$ , dann ist der Graph der Ableitungsfunktion $f'$ achsensymmetrisch zur Achse $x=a$ .
Ist der Graph einer Funktion $f$ achsensymmetrisch zur Achse $x=a$ , dann ist der Graph der Ableitungsfunktion $f'$ punktsymmetrisch zum Punkt $\left(a,0\right)$ .

Beispiele

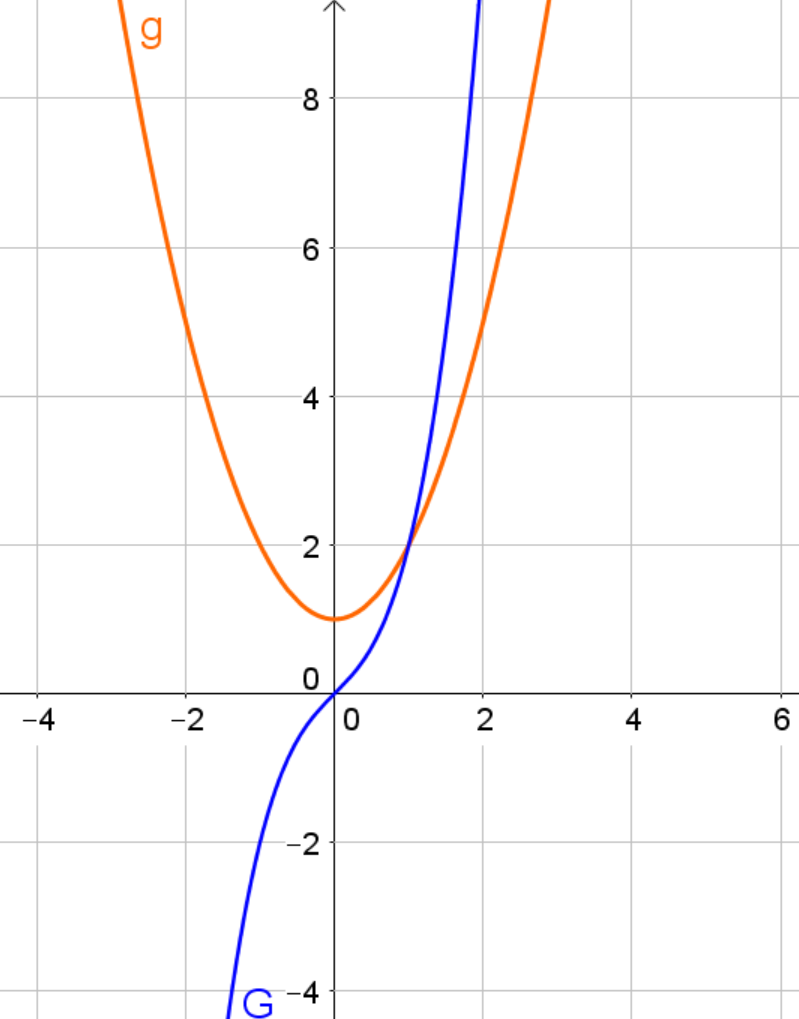
Der braune Graph der Funktion $q$ ist punktsymmetrisch zum Ursprung. Der grüne Graph der Ableitungsfunktion $q'$ ist eine Parabel, die achsensymmetrisch zur $y$ -Achse ist.

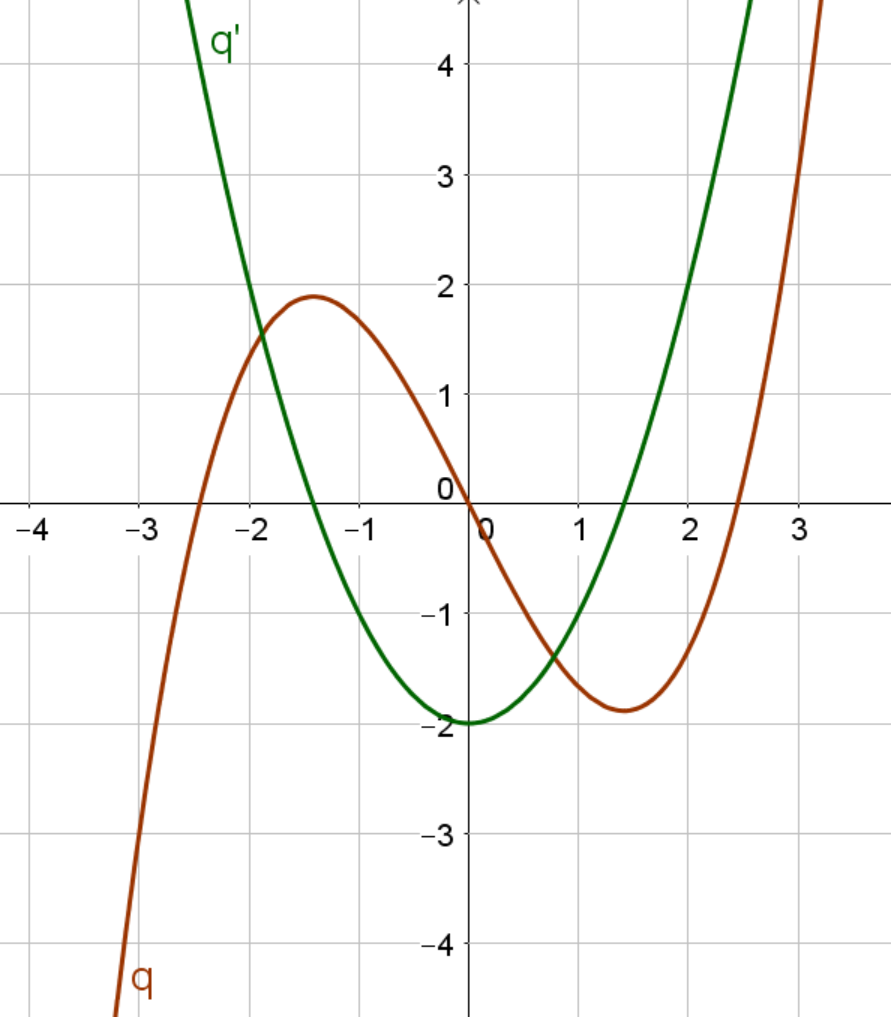
Der rote Graph der Funktion $f$ ist achsensymmetrisch zur $y$ -Achse. Leitet man $f$ ab, so erhält man $f',$ dessen Graph du hier in dunkelblau sehen kannst. Der Graph von der Ableitungsfunktion $f'$ ist punktsymmetrisch zum Ursprung.

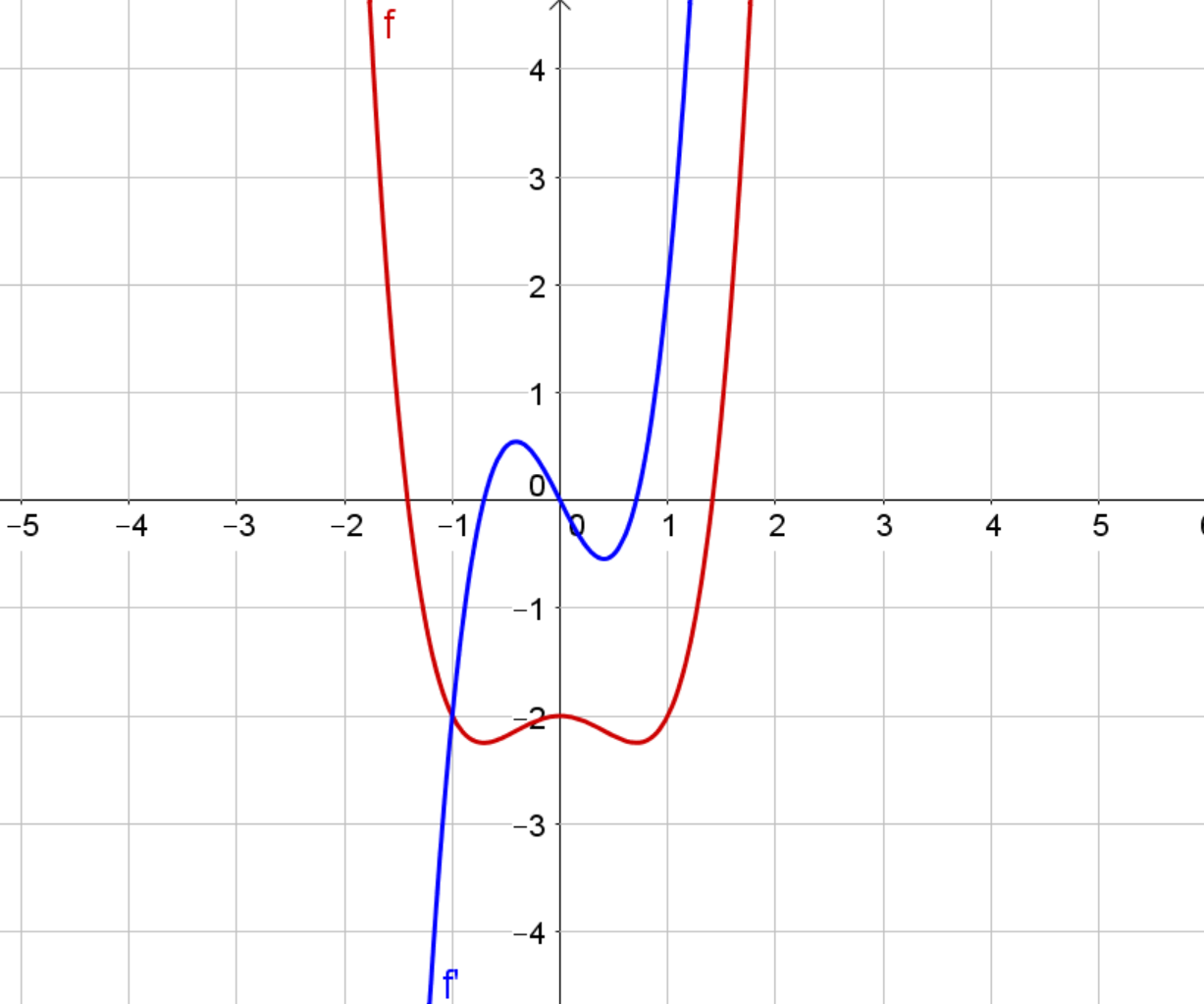
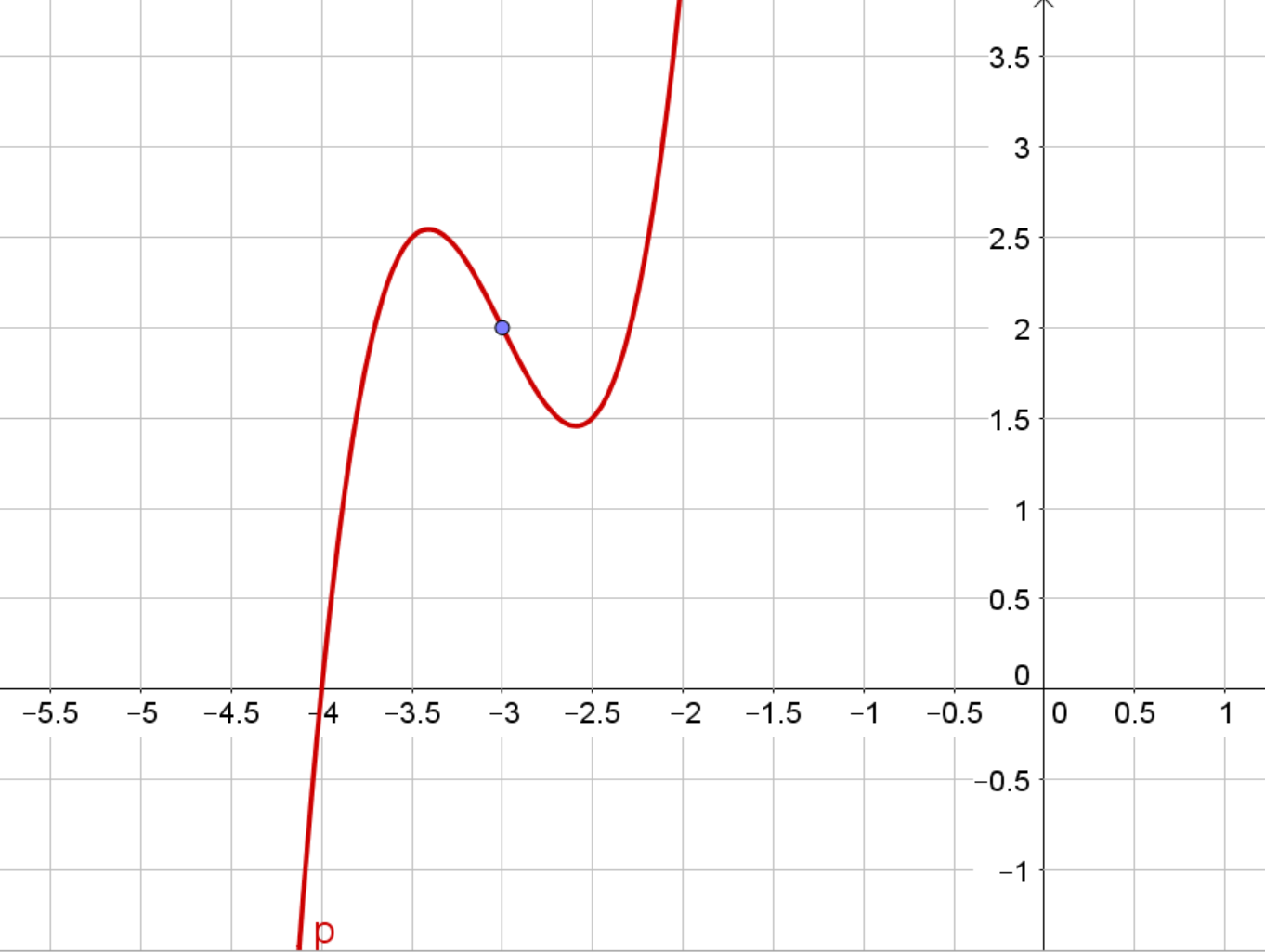
Der Graph der Funktion $k$ ist hier in orange zu sehen. Er ist punktsymmetrisch zum markierten Punkt $\left(-2,\ -3\right)$ . Leitet man $k$ ab, so erhält man die Ableitungsfunktion $k'$ . Ihr Graph ist in lila dargestellt. Der Graph von $k'$ ist eine Parabel, die achsensymmetrisch zur Achse $x=-2$ ist. Die $x$ -Koordinate des Symmetriepunktes von $k$ entspricht also genau der Symmetrieachse der Ableitungsfunktion $k'$ .

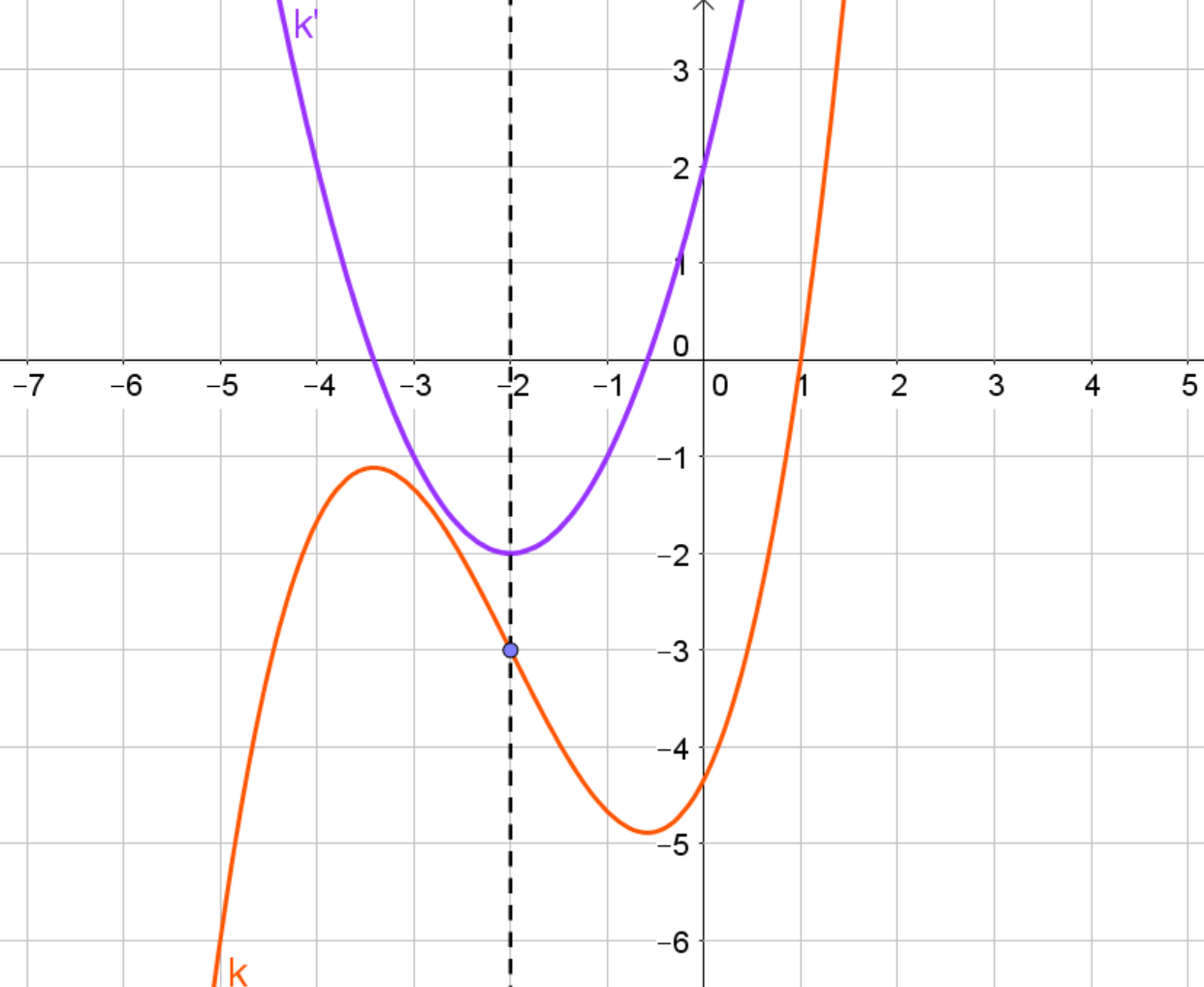
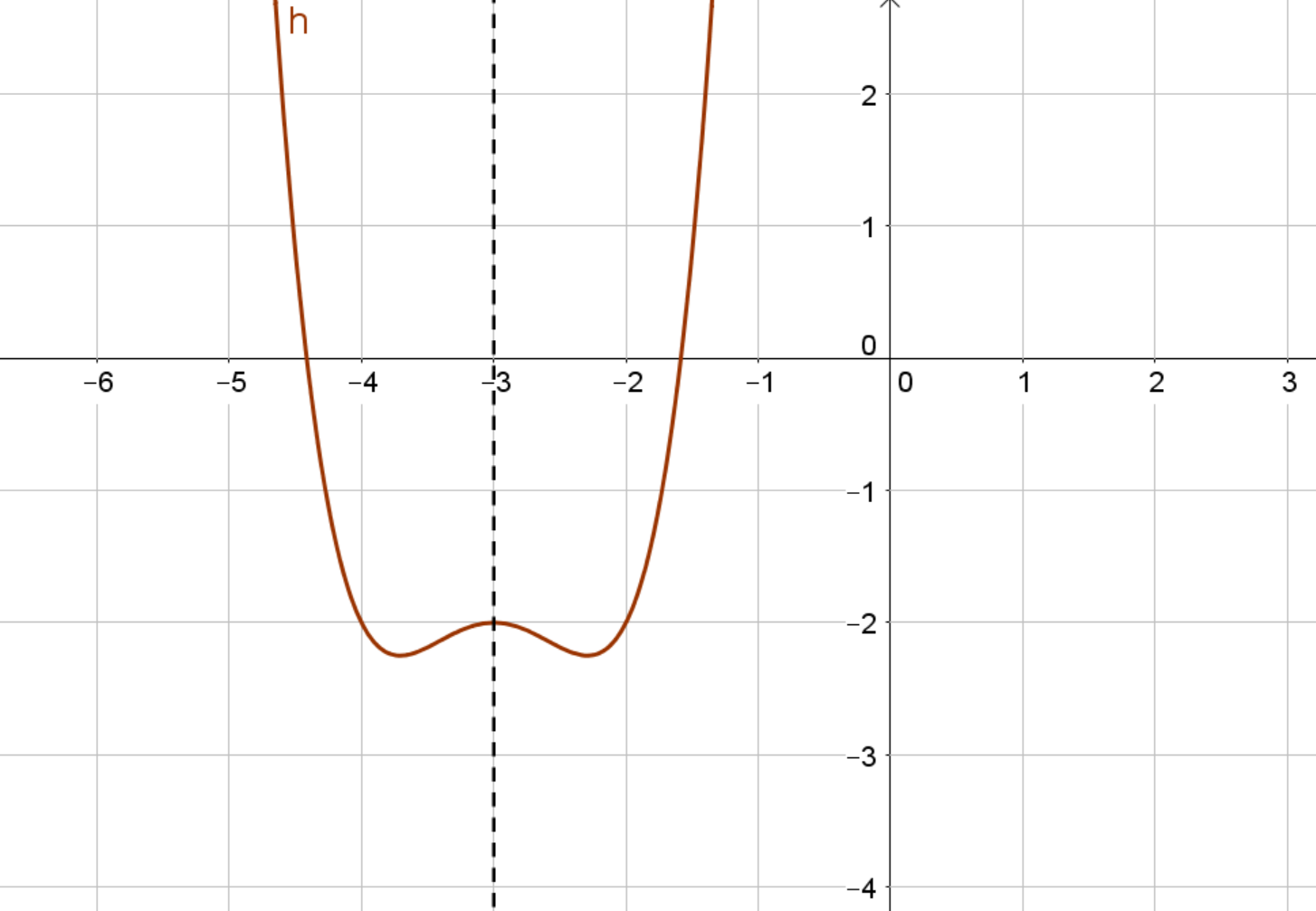
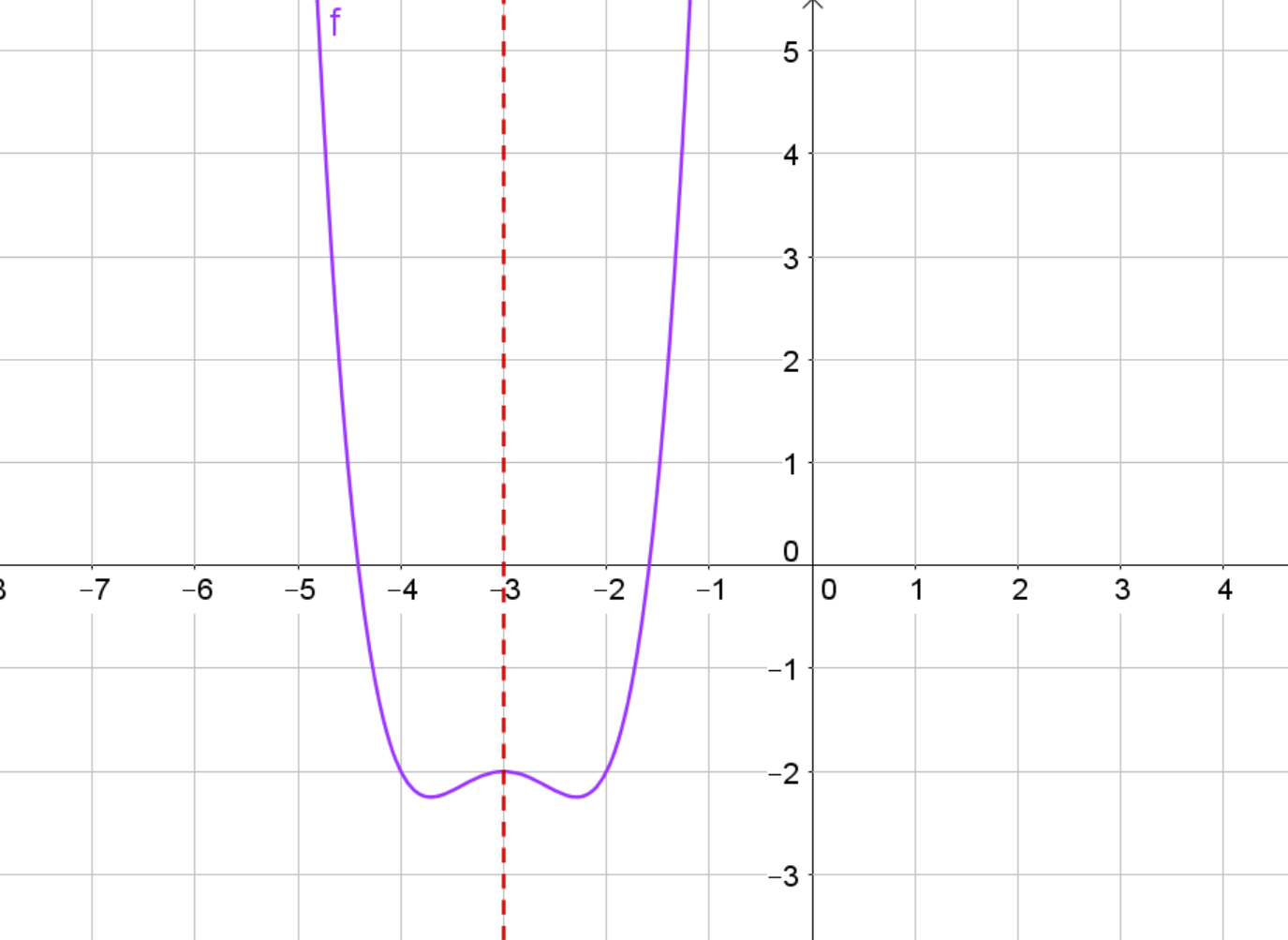
Der braune Graph der Funktion $h$ ist achsensymmetrisch zur Achse $x=-3$ . Indem du $h$ ableitest, erhältst du $h'$ . Den Graphen von $h'$ kannst du hier in dunkelgrün sehen. Du siehst, dass $h'$ punktsymmetrisch zum Punkt $\left(-3{,}0\right)$ ist. Die $x$ -Koordinate dieses Punktes liegt genau auf der Symmetrieachse von $h$ . Die $y$ -Koordinate des Symmetriepunktes ist $0.$

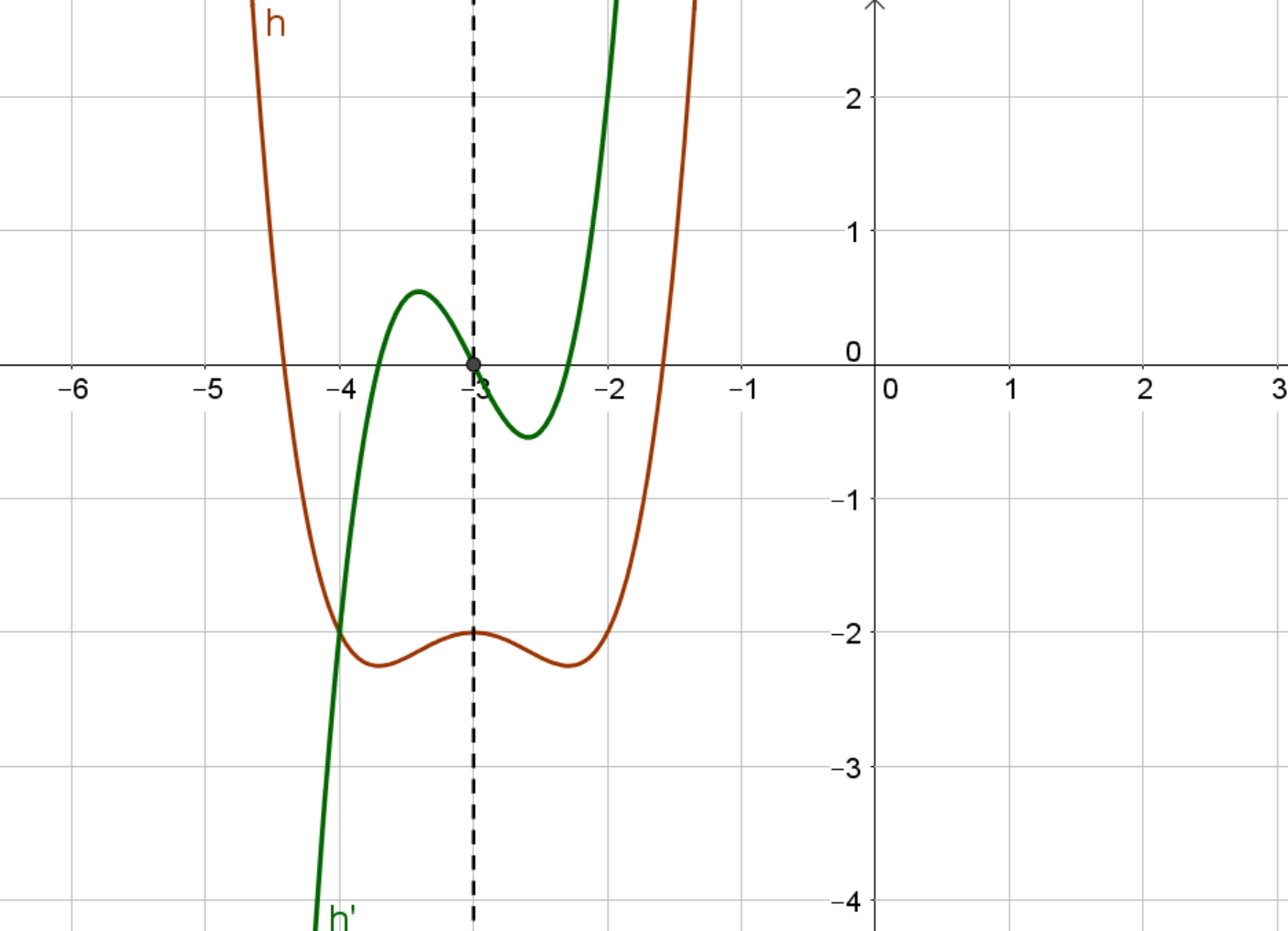
Symmetrie von Stammfunktionen

Merke

Ist der Graph einer Funktion $f$ punktsymmetrisch zum Ursprung, dann ist der Graph der Stammfunktion $F$ achsensymmetrisch zur $y$ -Achse.
Ist der Graph einer Funktion $f$ achsensymmetrisch zur $y$ -Achse, dann ist der Graph der Stammfunktion $F$ punktsymmetrisch zu irgendeinem Punkt auf der $y$ -Achse (also nicht zwingend zum Ursprung).

Allgemein gilt:

Aus der Punktsymmetrie des Graphen von $f$ zu einem allgemeinen Punkt lassen sich keine allgemeinen Symmetrieregeln für den Graphen von $F$ ableiten.
Ist der Graph von $f$ achsensymmetrisch zu einer Achse $x=a$ , dann ist der Graph von $F$ punktsymmetrisch zu einem Punkt, der auf dieser Symmetrieachse liegt, d.h. zum Punkt $\left(a,\ d\right)$ . Dabei ist $d$ eine "wählbare" $y$ -Koordinate, die von der Verschiebung der Stammfunktion in $y$ -Richtung abhängt.

Beispiele

Die Parabel $g$ ist achsensymmetrisch zur $y$ -Achse. Eine zugehörige Stammfunktion $G$ ist hier in dunkelblau dargestellt. Diese ist punktsymmetrisch zum Ursprung. Allerdings dürfen wir $G$ aufgrund der Integrationskonstante beliebig in $y$ -Richtung nach oben und unten verschieben. $G$ könnte daher also beispielsweise bei Verschiebung um $2$ Einheiten nach oben auch punktsymmetrisch zum Punkt $\left(0{,}2\right)$ sein. Aber egal, um wie viel wir $G$ nach oben und unten verschieben: die $x$ -Koordinate des Symmetriepunkts liegt stets auf der $y$ -Achse.

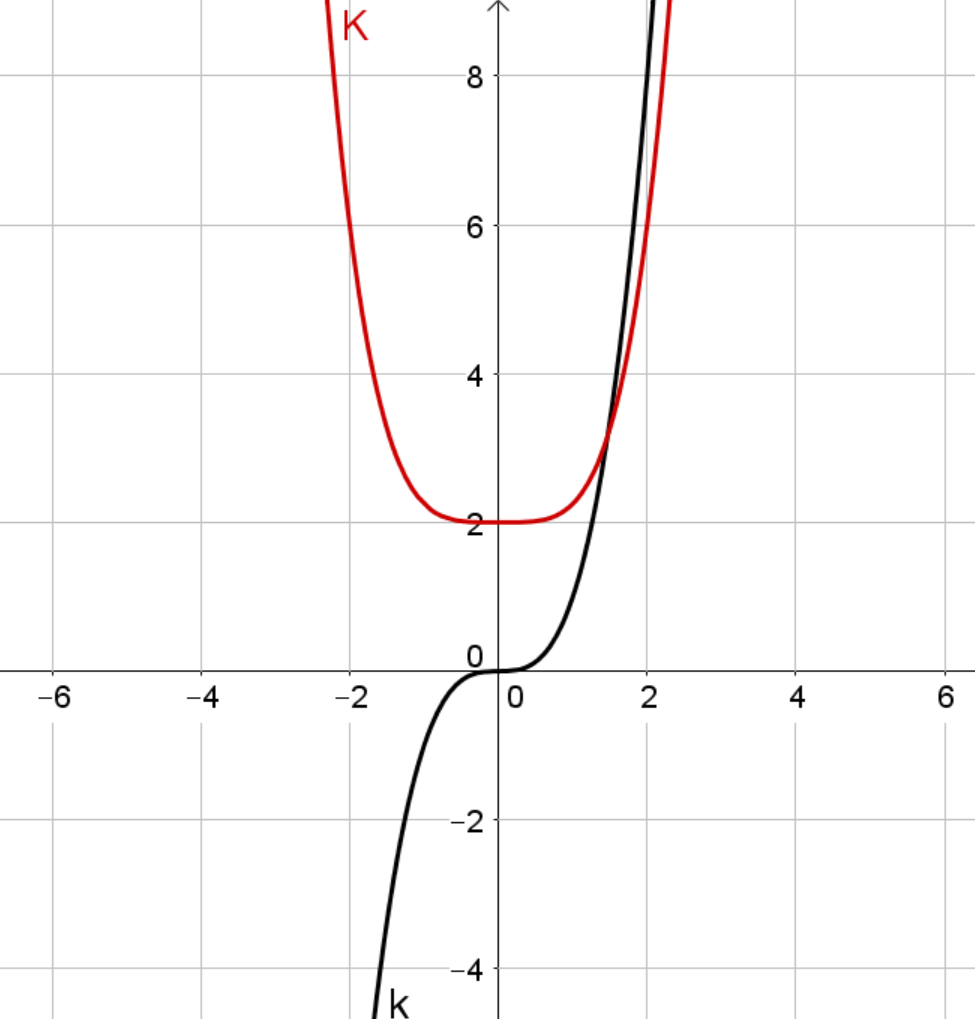
Die in schwarz dargestellte Funktion $k$ ist punktsymmetrisch zum Ursprung. $K$ ist eine mögliche Stammfunktion von $k$ . Diese ist achsensymmetrisch zur $y$ -Achse.

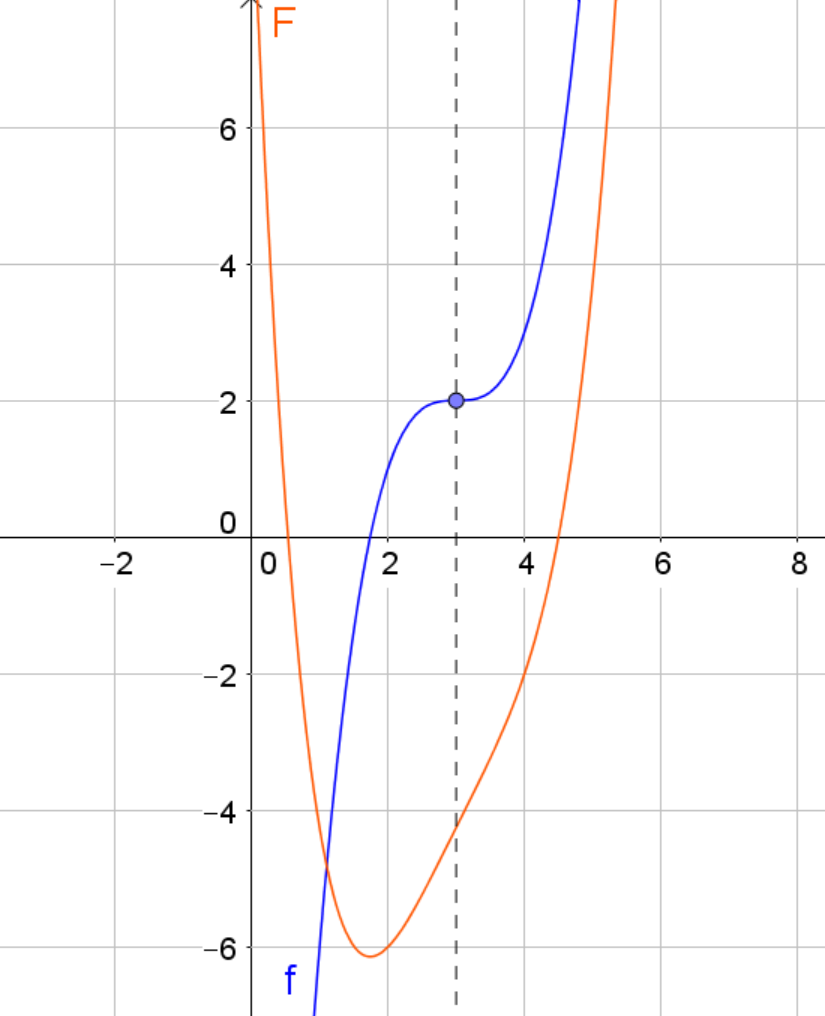
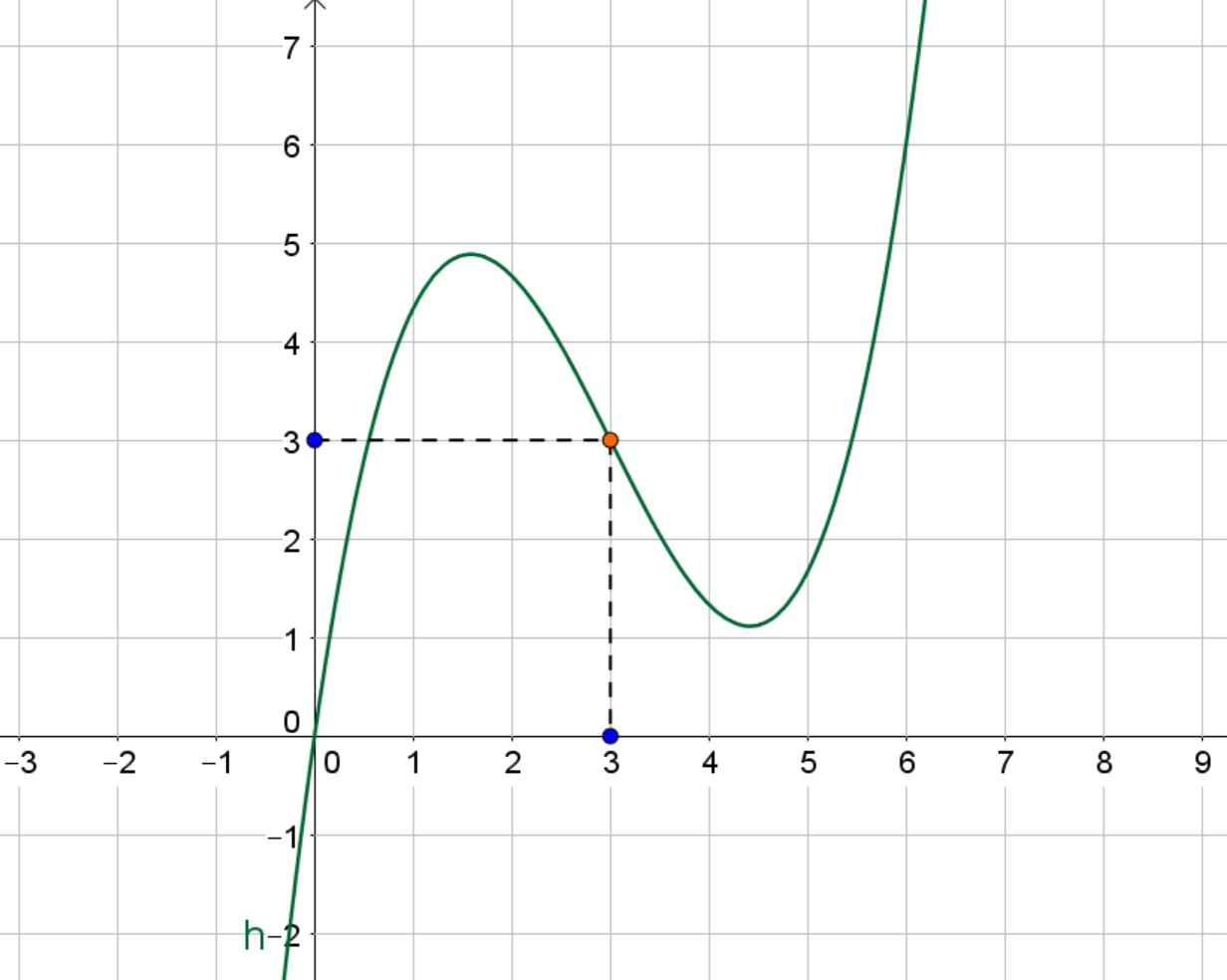
Die hier blau dargestellte Funktion $f$ ist punktsymmetrisch zum Punkt $\left(3{,}2\right)$ . Eine mögliche Stammfunktion $F$ kannst du in orange sehen. $F$ ist weder achsensymmetrisch noch punktsymmetrisch zu einem beliebigen Punkt - unabhängig davon, wie man die Stammfunktion nach oben und unten in $y$ -Richtung verschiebt.

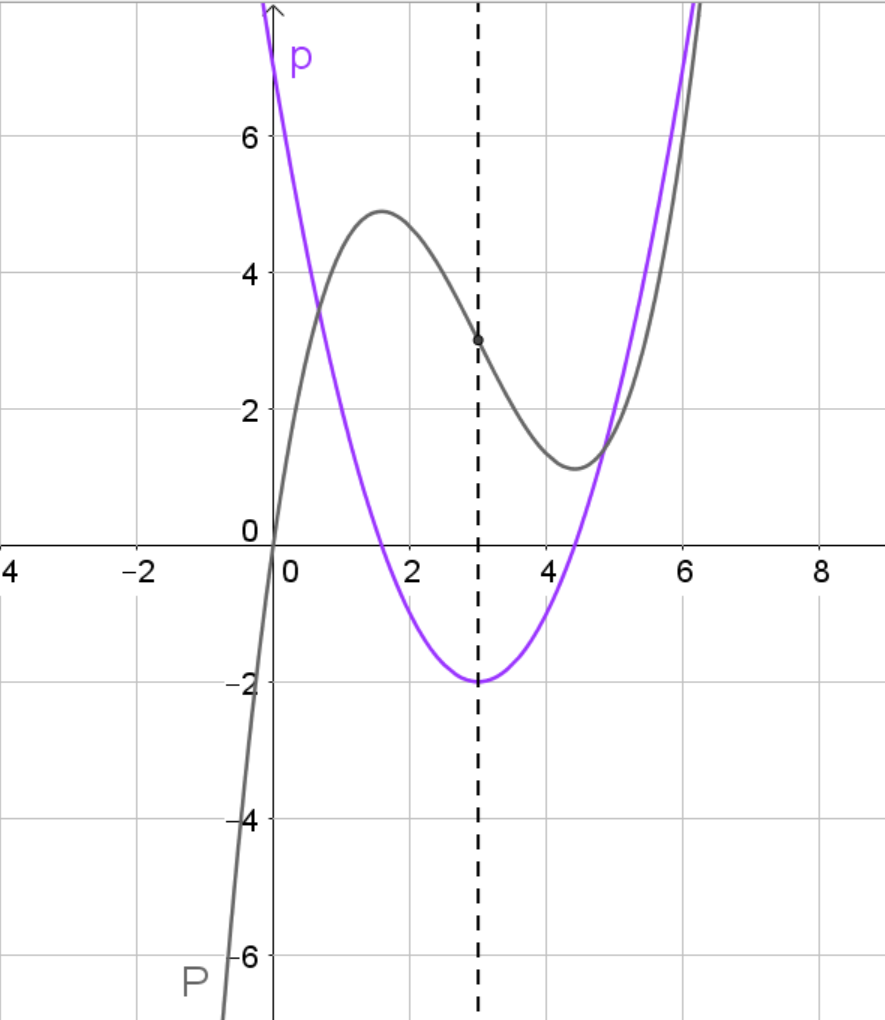
Die lila Parabel $p$ ist achsensymmetrisch zur Achse $x=3$ . Eine zugehörige Stammfunktion $P$ (hier in grün) ist punktsymmetrisch zum Punkt $\left(3{,}3\right)$ . Du darfst $P$ aufgrund der Integrationskonstante beliebig in $y$ -Richtung nach oben und unten verschieben. Dann ändert sich die $y$ -Koordinate des Symmetriepunktes, aber die $x$ -Koordinate wird immer bei $3$ bleiben - also auf der Symmetrieachse der Parabel liegen.

Allgemeine Symmetrie

Der Graph einer Funktion $f$ kann im Allgemeinen nicht nur achsensymmetrisch zur $y$ -Achse, sondern auch zu einer beliebig anderen senkrechten Achse achsensymmetrisch sein.

Beispielsweise ist die Funktion $h$ achsensymmetrisch zur Achse $x=-3$ .

Analog kann der Graph einer Funktion $f$ auch zu einem beliebigen anderen Punkt - als nur zum Ursprung - punktsymmetrisch sein.

Zum Beispiel ist die Funktion $p$ punktsymmetrisch zum Punkt $\left(-3{,}2\right)$ .

Überprüfung, ob $f$ zu einer bekannten allgemeinen Achse achsensymmetrisch ist

Merke

Ist der Graph einer Funktion $f$ achsensymmetrisch zur Achse $x=c$ , dann gilt:

\displaystyle f(-x)=f(x)

Die y-Achse ist der Spezialfall $c=0$ .

Vorgehen

Wenn du also überprüfen sollst, ob eine Funktion zu einer gegebenen Achse achsensymmetrisch ist, dann kannst du folgendes tun:

Du setzt $\left(c-x\right)$ in den Funktionsterm für $x$ ein und rechnest aus.
Dann setzt du $\left(c+x\right)$ in den Funktionsterm für $x$ ein und rechnest aus.
Du vergleichst deine Ergebnisse aus 1. und 2.. Sind diese gleich, dann ist $f$ achsensymmetrisch zur Achse $x=c$ . Kommt bei 1. und 2. etwas Unterschiedliches heraus, dann ist $x=c$ keine Symmetrieachse von $f$ .

Beispiel

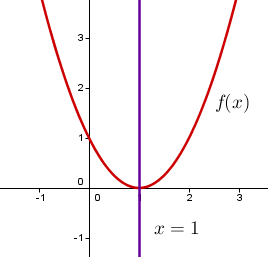
Überprüfe, ob die Funktion $f:x \mapsto x^2-2x+1$ achsensymmetrisch zur Achse $x=1$ ist.

Als Erstes berechnen wir $f\left(1-x\right)$ .

Dafür setzen wir $\left(1-x\right)$ in den Funktionsterm ein
	↓
$\displaystyle f\left(1-x\right)$	$=$	$\displaystyle \left(1-x\right)^2-2\left(1-x\right)+1$
	↓	Wir wenden die binomische Formel an und multiplizieren aus
	$=$	$\displaystyle 1-2x+x^2-2+2x+1$
	↓	Nun fassen wir zusammen
	$=$	$\displaystyle x^2-2x+2x+1+1-2$
	$=$	$\displaystyle x^2$

Also ist $f\left(1-x\right)=x^2$ .

Als Nächstes berechnen wir $f\left(1+x\right)$ .

Dafür setzen wir $\left(1+x\right)$ in den Funktionsterm ein
	↓
$\displaystyle f\left(1+x\right)$	$=$	$\displaystyle \left(1+x\right)^2-2\left(1+x\right)+1$
	↓	Wir wenden die binomische Formel an und multiplizieren aus
	$=$	$\displaystyle 1+2x+x^2-2-2x+1$
	↓	Nun fassen wir zusammen
	$=$	$\displaystyle x^2$

Also ist $f\left(1+x\right)=x^2$ .

Sowohl $f\left(1-x\right)=x^2$ als auch $f\left(1+x\right)=x^2$ . Weil bei beiden dasselbe herauskommt, ist $f$ tatsächlich achsensymmetrisch zur Achse $x=1$ .

Überprüfung, ob $f$ zu einem bekannten allgemeinen Punkt punktsymmetrisch ist

Merke

Ist der Graph der Funktion $f$ punktsymmetrisch zum Punkt $P\left(a,\ b\right)$ , gilt:

\displaystyle f(-x)=f(x)

Der Ursprung ist der Spezialfall $P(0,\ 0)$ .

Vorgehen

Wenn du also überprüfen sollst, ob eine Funktion zu einem gegebenen Punkt punktsymmetrisch ist, dann kannst du folgendes tun:

Berechne $f\left(a-x\right)-b$ , indem du in den Funktionsterm $\left(a-x\right)$ für $x$ einsetzt und anschließend $b$ , also die $y$ -Koordinate des Punktes abziehst.
Berechne $-f\left(a+x\right)+b$ , indem du in den Funktionsterm $\left(a+x\right)$ für $x$ einsetzt, den Funktionsterm mit $\left(-1\right)$ multiplizierst und anschließend $b$ , also die $y$ -Koordinate des Punktes addierst.
Vergleiche die Ergebnisse aus 1. und 2.. Sind diese gleich, dann ist die Funktion tatsächlich punktsymmetrisch zu $P$ . Sind die Ergebnisse unterschiedlich, ist $f$ nicht punktsymmetrisch zu $P$ .

Beispiel

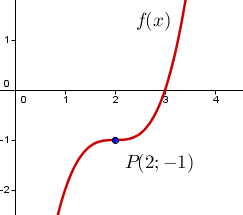
Prüfe, ob die Funktion $f: x\mapsto \left(x-2\right)^3-1$ punktsymmetrisch zum Punkt $P(2,\ -1)$ ist.

Als Erstes berechnen wir $f\left(a-x\right)-b=f\left(2-x\right)+1$

Dafür setzen wir im Funktionsterm $\left(2-x\right)$ für $x$ ein und addieren am Ende noch $1$
	↓
$\displaystyle f\left(2-x\right)+1$	$=$	$\displaystyle \left(2-x-2\right)^3-1+1$
	↓	Vereinfachen
	$=$	$\displaystyle \left(-x\right)^3$
	$=$	$\displaystyle -x^3$

Also ist $f\left(2-x\right)+1=-x^3$ .

Als Nächstes berechnen wir $-f\left(a+x\right)+b=-f\left(2+x\right)-1$

Dafür setzen wir $\left(2+x\right)$ für $x$ ein, multiplizieren den Funktionsterm mit $\left(-1\right)$ und ziehen ab Schluss noch die $1$ ab.
	↓
$\displaystyle -f\left(2+x\right)-1$	$=$	$\displaystyle -\left(\left(2+x-2\right)^3-1\right)-1$
	↓	Vereinfachen
	$=$	$\displaystyle -\left(x^3-1\right)-1$
	↓	Jetzt lösen wir die Minusklammer auf
	$=$	$\displaystyle -x^3+1-1$
	$=$	$\displaystyle -x^3$

Also ist $-f\left(2+x\right)-1=-x^3$ , genauso wie $f\left(2-x\right)+1=-x^3$ . Deswegen ist $f$ punktsymmetrisch zu $\left(2,\ -1\right)$ .

Geogebra File: https://assets.serlo.org/legacy/8870_BNJuhm1LmI.xml

Allgemeine Symmetrieachse eines Funktionsgraphen berechnen

1) Berechnung für Polynomfunktionen

Nur Polynomfunktion geraden Grades $n$ kommen für Achsensymmetrie infrage.

Vorgehen

Um die Symmetrieachse $x=a$ des Graphen von $f$ zu berechnen, gehen wir wie folgt vor:

Berechne die $\left(n-1\right)$ -te Ableitung von $f$
Berechne die Nullstelle der $\left(n-1\right)$ -ten Ableitung. Die $x$ -Werte der Nullstelle $a$ entspricht potentiell der Symmetrieachse $x=a$ von $f$
Proberechnung: Überprüfe mit $f\left(a-x\right)=f\left(a+x\right)$ , ob $f$ auch wirklich achsensymmetrisch zu der errechneten Achse ist.

Hinweis: Die Proberechnung ist in diesem Fall unerlässlich, weil wir zu Beginn der Rechnung gar nicht wissen, ob der Graph von $f$ überhaupt achsensymmetrisch ist.

Beispiel

Wir wollen die Symmetrieachse der Funktion $f:x \mapsto x^4+12x^3+53x^2+102x+70$ berechnen.

Die Funktion ist $4$ . Grades, deshalb berechnen wir nun die $\left(4-1\right)$ -te Ableitung, also die $3$ . Ableitung:

$f'\left(x\right)=4x^3+36x^2+106x+102$

$f''\left(x\right)=12x^2+72x+106$

$f'''\left(x\right)=24x+72$

Als Nächstes berechnen wir die Nullstelle der dritten Ableitung:

$\displaystyle 24x+72$	$=$	$\displaystyle 0$	$\displaystyle -72$
$\displaystyle 24x$	$=$	$\displaystyle -72$	$\displaystyle :24$
$\displaystyle x$	$=$	$\displaystyle -3$

Eine mögliche Symmetrieachse von $f$ ist also $x=-3$ .

Durch eine Proberechnung mit $f\left(3-x\right)=f\left(3+x\right)$ können wir feststellen, dass es sich hierbei wirklich um die Symmetrieachse von $f$ handelt.

2) Berechnung für gebrochenrationale Funktionen

Hier fehlt noch eine Erklärung der Berechnung der Achsensymmetrie von gebrochenrationalen Funktionen.

Allgemeinen Symmetriepunkt eines Funktionsgraphen berechnen

1) Berechnung für Polynomfunktionen

Nur Polynomfunktionen ungeraden Grades $n$ kommen für die Punktsymmetrie infrage.

Vorgehen

Um den Symmetriepunkt $\left(a,b\right)$ des Graphen von $f$ zu berechnen, gehen wir wie folgt vor:

Berechne die $\left(n-1\right)$ -te Ableitung von $f$
Berechne die Nullstelle der $\left(n-1\right)$ -ten Ableitung. Die Nullstelle $a$ ist die $x$ -Koordinate des potentiellen Symmetriepunktes
Berechne $b=f\left(a\right)$
Proberechnung: Überprüfe mit $f\left(a-x\right)-b=-f\left(a+x\right)+b$ , ob es sich bei $\left(a,b\right)$ wirklich um den Symmetriepunkt von $f$ handelt.

Hinweis: Die Proberechnung ist in diesem Fall unerlässlich, weil wir zu Beginn der Rechnung gar nicht wissen, ob der Graph von $f$ überhaupt punktsymmetrisch ist.

Beispiel

Wir wollen berechnen, zu welchem Punkt der Graph der Funktion $h: x \mapsto \frac{1}{3}x^3-3x^2+7x$ punktsymmetrisch ist.

$h$ ist eine Polynomfunktion dritten Grades. Deshalb berechnen wir nun die $\left(3-1\right)$ -te Ableitung, also die zweite Ableitung:

$h'\left(x\right)=x^2-6x+7$

$h''\left(x\right)=2x-6$

Nun berechnen wir die Nullstelle der zweiten Ableitung:

$\displaystyle 2x-6$	$=$	$\displaystyle 0$	$\displaystyle +6$
$\displaystyle 2x$	$=$	$\displaystyle 6$	$\displaystyle :2$
$\displaystyle x$	$=$	$\displaystyle 3$

Die $x$ -Koordinate des potentiellen Symmetriepunktes ist also $a=3$ . Um die $y$ -Koordinate des Punktes zu erhalten, setzen wir die $x$ -Koordinate in $h$ ein:

$\displaystyle h\left(3\right)$	$=$	$\displaystyle \frac{1}{3}\cdot3^3-3\cdot3^2+7\cdot3$
	$=$	$\displaystyle 9-27+21$
	$=$	$\displaystyle 3$

Der mögliche Symmetriepunkt von $h$ ist also $\left(3{,}3\right)$ .

Durch eine Proberechnung mit $h\left(3-x\right)-3=-h\left(3+x\right)+3$ können wir feststellen, dass es sich hierbei wirklich um den Symmetriepunkt von $h$ handelt.

2) Berechnung für gebrochenrationale Funktionen

Hier fehlt noch eine Erklärung der Berechnung der Punktsymmetrie von gebrochenrationalen Funktionen.

Übungsaufgaben

Inhalt wird geladen…

Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zur Symmetrie von Graphen

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0. → Was bedeutet das?

Symmetrie von Graphen

Bestimmung der Symmetrie

Beispiele

Hilfreiche Regel für Polynomfunktionen

Beispiele

Video zur Symmetrie

Hilfreiche Regel für gebrochenrationale Funktionen

Beispiele

Symmetrie von Ableitungen und Stammfunktionen

Symmetrie von Ableitungen

Beispiele

Symmetrie von Stammfunktionen

Beispiele

Allgemeine Symmetrie

Überprüfung, ob fff zu einer bekannten allgemeinen Achse achsensymmetrisch ist

Beispiel

Überprüfung, ob fff zu einem bekannten allgemeinen Punkt punktsymmetrisch ist

Beispiel

Allgemeine Symmetrieachse eines Funktionsgraphen berechnen

1) Berechnung für Polynomfunktionen

Beispiel

2) Berechnung für gebrochenrationale Funktionen

Allgemeinen Symmetriepunkt eines Funktionsgraphen berechnen

1) Berechnung für Polynomfunktionen

2) Berechnung für gebrochenrationale Funktionen

Übungsaufgaben

Überprüfung, ob $f$ zu einer bekannten allgemeinen Achse achsensymmetrisch ist

Überprüfung, ob $f$ zu einem bekannten allgemeinen Punkt punktsymmetrisch ist