Aufgaben zum Strahlensatz oder Vierstreckensatz

Berechne den Anteil der roten Fläche an der Trapezfläche. Beachte, dass das Trapez symmetrisch ist!

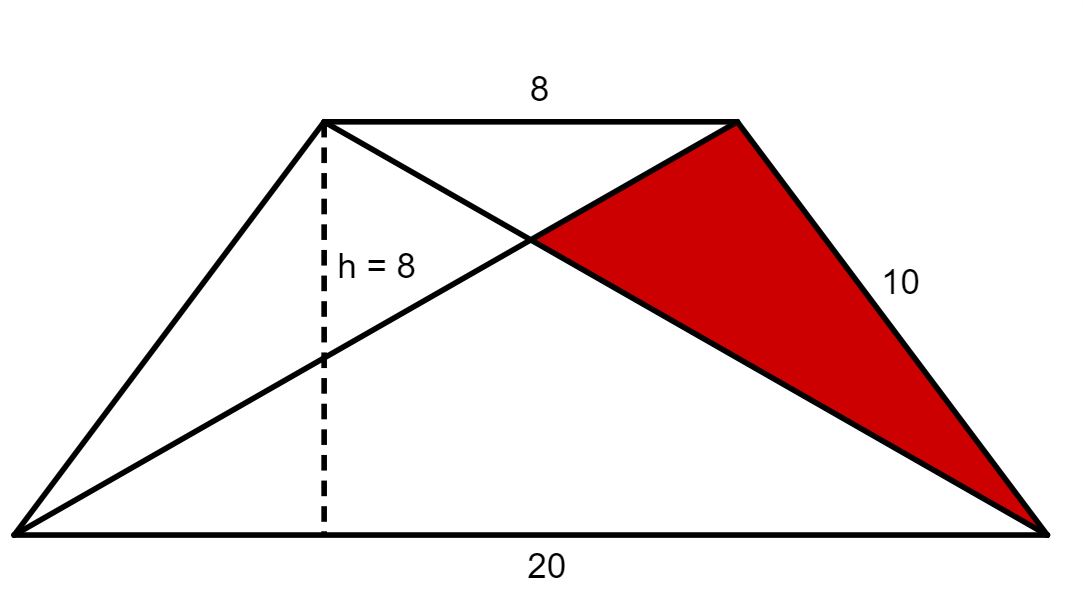
Für diese Aufgabe benötigst Du folgendes Grundwissen: Strahlensatz

Tipp: Berechne zunächst die Flächen des türkisen und des weißen Dreiecks um darüber auf die rote Fläche zu kommen!

Berechnen der Trapezfläche

Die Fläche des gesamten Trapezes kannst du schon mithilfe der angegebenen Werte berechnen. Diesen Wert brauchst du am Ende um den Anteil der roten Fläche zu bestimmen.

Die Fläche des Trapezes ist:

\displaystyle A_{Trapez}=\dfrac{1}{2} (a+c) \cdot h = \dfrac{1}{2}(20+8)\cdot 8 = 112

Berechnen der roten Fläche

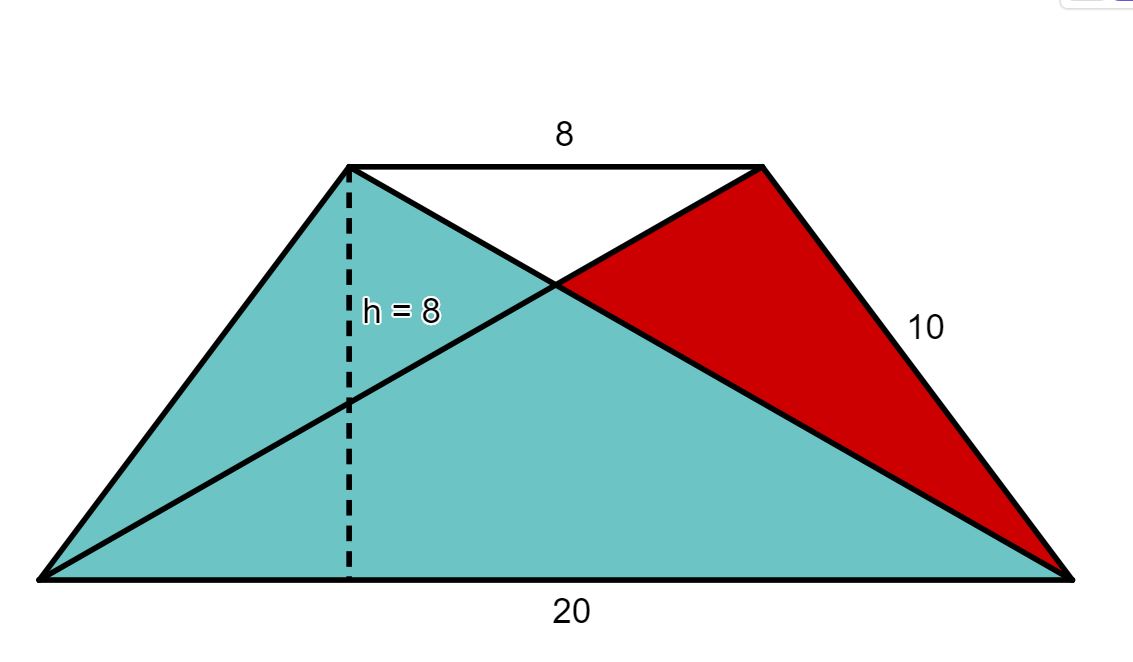
Um die rote Fläche berechnen zu können, hilft es sich das Dreieck in verschiedene Flächen aufzuteilen, wie in der Skizze eingezeichnet:

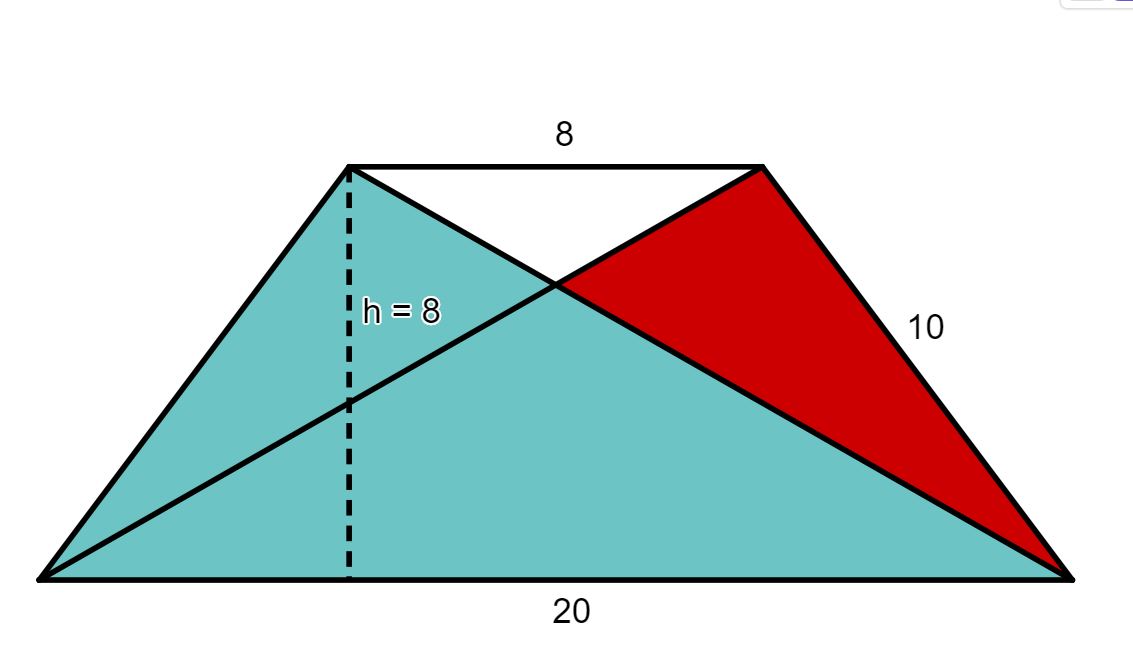
Anschließend kannst du die Flächen des türkisen und des weißen Dreiecks bestimmen und aus der Differenz der gesamten Fläche und der beiden kleinen Flächen den Wert der roten Fläche bestimmen.

Fläche des türkisen Dreiecks

Die Fläche des türkisen Dreiecks kannst du mithilfe der Grundseite ( $20$ ) und der Höhe ( $8$ ) bestimmen.

\displaystyle A_{Türkis}=\dfrac{1}{2}\cdot 20\cdot 8 = 80

Fläche des weißen Dreiecks

Die Grundseite des weißen Dreiecks hast du gegeben, die Höhe ist aber noch unbekannt. Diese kannst du aber mithilfe des ersten Strahlensatzes bestimmen. Dazu brauchst du allerdings noch eine weitere Streckenlänge, die in der Skizze mit $x$ bezeichnet wird.

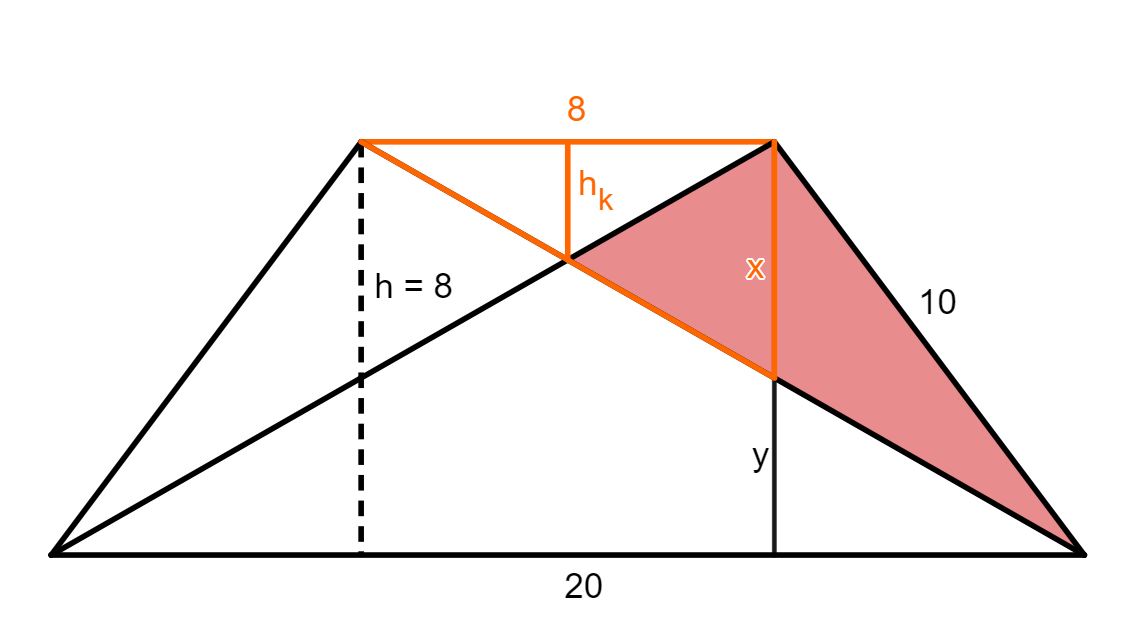
Du siehst eine (orange) $V$ -Figur, für die du den Strahlensatz wie folgt aufstellen kannst:

$\dfrac{h_k}{x}=\dfrac{4}{8}$

Die $4$ kommt dadurch zustande, dass das Trapez symmetrisch ist, die Höhe des weißen Dreiecks die Grundfläche also genau halbiert.

Zunächst musst du also die Länge der Strecke $x$ berechnen um anschließend auf die Länge von $h_{k}$ zu kommen.

Die Strecke $x$ ist genau $8 - y$ lang und $y$ kann wiederum mithilfe des Strahlensatzes berechnet werden.

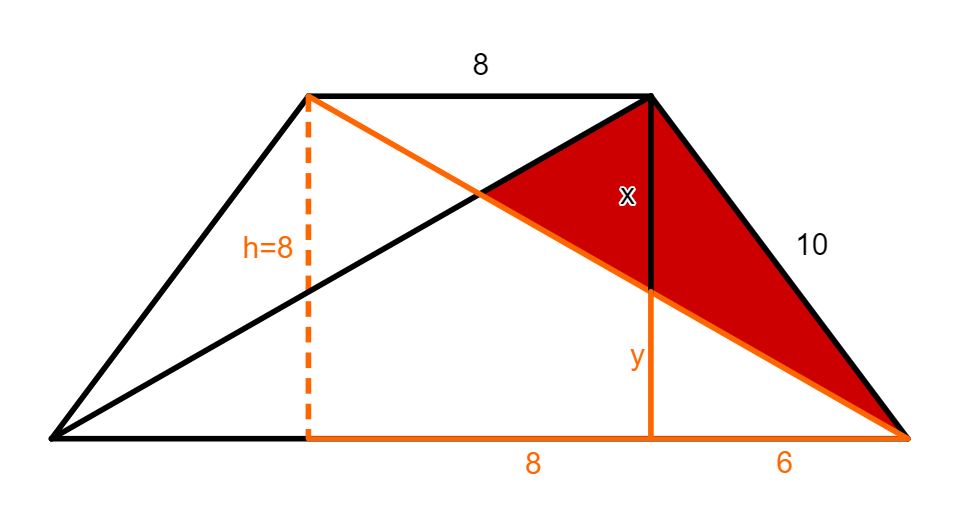
In der Skizze siehst du in orange die entsprechenden Strecken, die du benötigst um die Strecke $y$ zu berechnen. Diese orange Figur entspricht einer $V$ -Figur.

Es gilt also:

\displaystyle \dfrac{y}{8}= \dfrac{6}{6+8}

Stelle diese Formel nach $y$ um, indem du mit $8$ multiplizierst.

\displaystyle y = \dfrac{6}{14} \cdot 8 =3{,}43

Demnach ist $x$ :

\displaystyle x=8-y=8-3{,}43

\displaystyle x=4{,}57

Jetzt kannst du, wie oben bereits beschrieben den Strahlensatz erneut anwenden, um auf die Höhe $h_{k}$ des kleinen Dreiecks zu kommen.

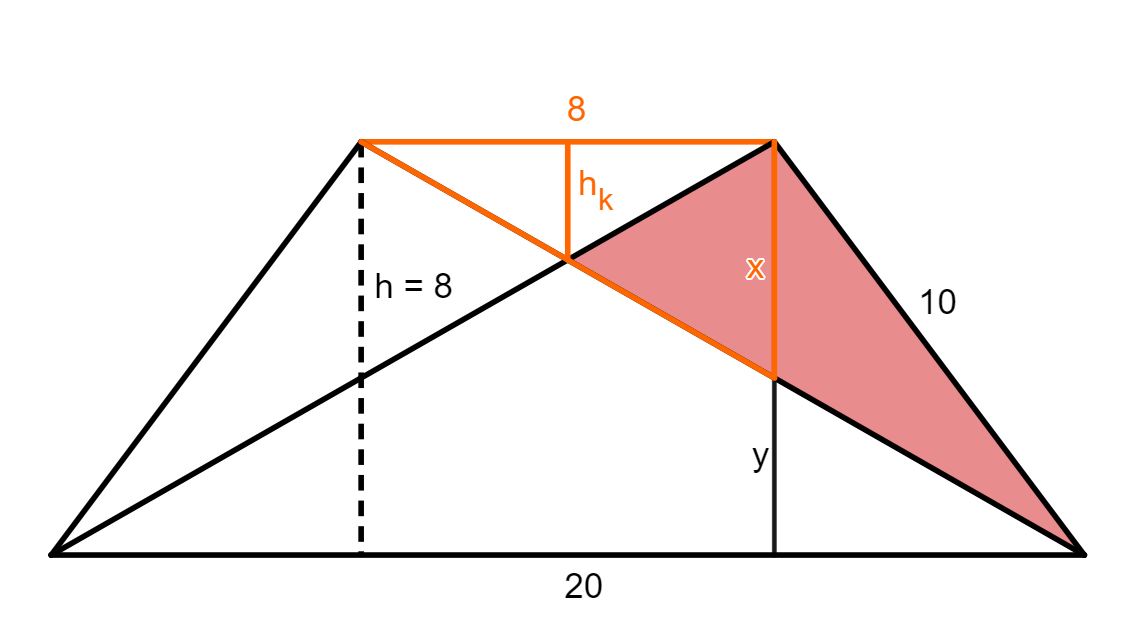
$h_{k}$ unterteilt die obere Strecke in zwei gleich große Teile mit der Länge $4$ , da es sich um ein symmetrisches Trapez handelt. Stelle nun den Strahlensatz für die $V$ -Figur auf, um $h_{k}$ zu berechnen.

\displaystyle \dfrac{h_k}{x} = \dfrac{4}{8}

Löse diese Gleichung nach $h_{k}$ auf, indem du mit $x$ multiplizierst.

\displaystyle h_k = \dfrac{4}{8} \cdot x

\displaystyle h_k = \dfrac{4}{8} \cdot 4{,}57 \approx 2{,}29

Jetzt kannst du mithilfe der Formel für die Fläche von Dreiecken die Fläche des weißen Dreiecks berechnen.

$A_{weiß} = \dfrac{1}{2} \cdot 8 \cdot 2{,}29 = 9{,}16$

Berechnung der roten Fläche

Die rote Fläche ergibt sich nun aus der Differenz des gesamten Trapezes und der beiden kleinen Dreiecke.

\displaystyle A_{rot}=A_{Trapez}-A_{türkis}-A_{weiß}

\displaystyle A_{rot}= 112 - 80 -9{,}16=22{,}84

Der Anteil der roten Fläche an der Gesamtfläche ist das folgende Verhältnis:

\displaystyle \dfrac{A_{rot}}{A_{Trapez}} = \dfrac{22{,}84}{112} = 0{,}2039

\displaystyle \dfrac{A_{rot}}{A_{Trapez}} = 20{,}39\%

Die rote Fläche macht $20{,}39 \%$ der Gesamtfläche aus.

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?