Dieser Artikel befindet sich im Sandkasten und wurde daher nicht auf Korrektheit geprüft! Sieh dir gern den folgenden, geprüften Artikel auf serlo.org an, wenn du mehr zum Thema wissen möchtest: indirekte Proportionalität
Grundwissen: Um eine antiproportionale Funktion zu verstehen, sollte man sich erst mit der proportionale Funktion vertraut machen.
Definition: Zwischen zwei Größen x und y besteht eine antiproportionale Zuordnung, wenn dem Doppelten (3-fachen,….-fachen) der eine Größe die Hälfte (ein Drittel, ein ….-tel) der anderen Größe zugeordnet ist.
Wertetabelle: An diesem Beispiel wird die Zuordnung verdeutlicht.
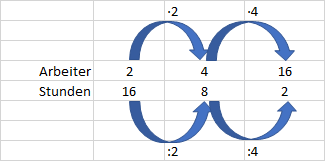
An diesem Beispiel kann man die antiproportional Zuordnung erkennen, denn je mehr Arbeiter zur Verfügung stehen, umso weniger Stunden benötigen sie, um eine x-beliebige Arbeit zu verrichten
Antiproportionalitätsfaktor: Das Produkt aus x (Arbeiter) und y (Stunden) ist der Antiproportionalitätsfaktor, der stets konstant bleibt. Somit kann man weitere Werte ohne Wertetabelle errechnen, wenn man den Faktor weiß.
Graph zur Wertetabelle: Zeichnet man die Wertepaare in ein Koordinatensystem, so erhält man eine Hyperbel. Aber Vorsicht eine proportionale Funktion könnte auch Hyperbel ähnlich Aussehen.
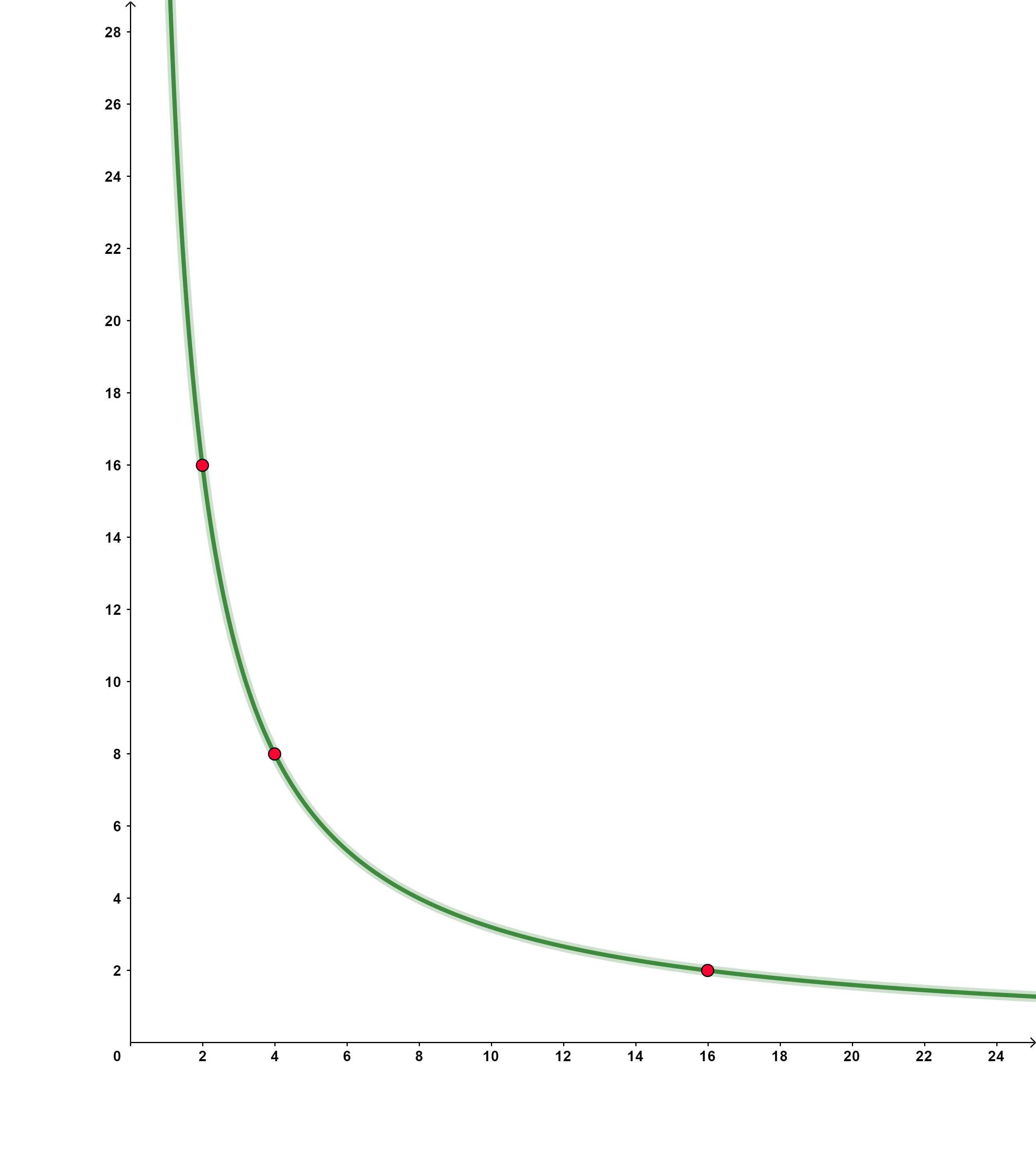
Merksatz: Je größer der x-Wert, desto kleiner der y-Wert!
Wenn noch Hilfebedarf besteht, kann man sich hier noch ein Video anschauen:
