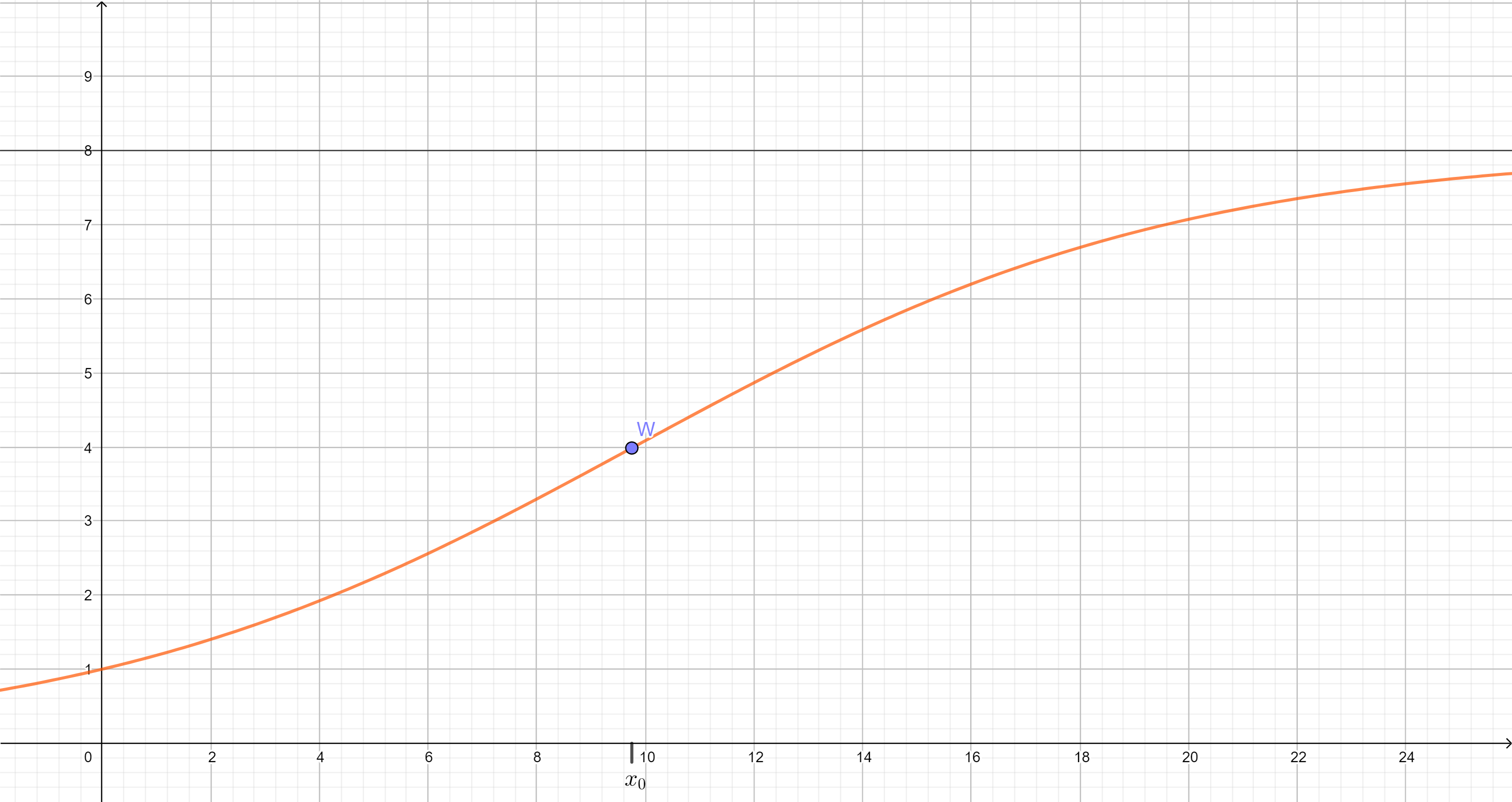
Die in definierte Funktion beschreibt modellhaft die zeitliche Entwicklung des Flächeninhalts eines Algenteppichs am Südufer eines Sees. Dabei ist die seit Beobachtungsbeginn vergangene Zeit in Tagen und der Flächeninhalt in Quadratmetern.
Bestimmen Sie sowie und geben Sie jeweils die Bedeutung des Ergebnisses im Sachzusammenhang an. Begründen Sie mithilfe des Monotonieverhaltens der Funktion , der Flächeninhalt des Algenteppichs im Laufe der Zeit ständig zunimmt.
Bestimmen Sie denjenigen Wert , für den gilt, und interpretieren Sie Ihr Ergebnis im Sachzusammenhang.
(zur Kontrolle: )
Bestimmen Sie die momentane Änderungsrate des Flächeninhalts des Algenteppichs zu Beobachtungsbeginn.
Nur zu dem Zeitpunkt, der im Modell durch (vgl. Aufgabe 2b) beschrieben wird, nimmt die momentane Änderungsrate des Flächeninhalts des Algenteppichs ihren größten Wert an. Geben Sie eine besondere Eigenschaft des Graphen von im Punkt an, die sich daraus folgern lässt, und begründen Sie ihre Angabe.
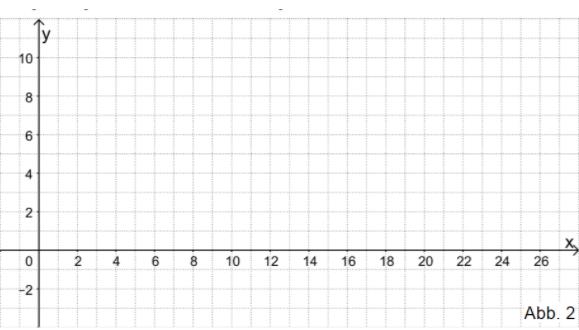
Skizzieren Sie den Graphen der Funktion unter Verwendung der bisherigen Ergebnisse in der Abbildung 2.
Um die zeitliche Entwicklung des Flächeninhalts eines Algenteppichs am Nordufer des Sees zu beschreiben, wird im Term die im Exponenten zur Basis e enthaltene Zahl durch eine kleinere Zahl ersetzt. Vergleichen Sie den Algenteppich am Nordufer mit dem am Südufer
• hinsichtlich der durch und beschriebenen Eigenschaften (vgl.
Aufgabe 2a).
• hinsichtlich der momentanen Änderungsrate des Flächeninhalts zu
Beobachtungsbeginn (vgl. Aufgabe 2c).
Skizzieren Sie – ausgehend von diesem Vergleich – in der Abbildung 2 den Graphen einer Funktion, die eine mögliche zeitliche Entwicklung des Flächeninhalts des Algenteppichs am Nordufer beschreibt.