Analysis, Teil B, Aufgabengruppe 2

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

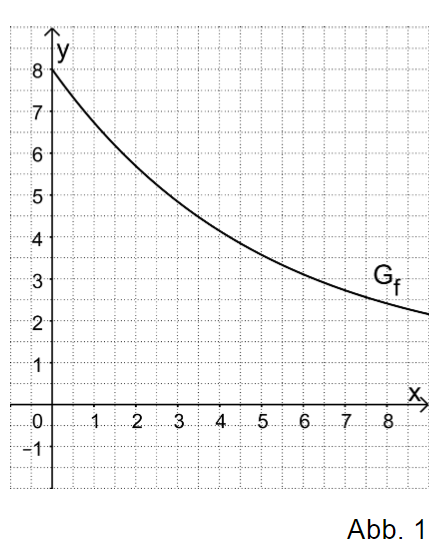
Gegeben ist die Funktion $f: x \mapsto 1+7e^{-0{,}2x}$ mit Definitionsbereich $\R^+_0$ ; die Abbildung 1 zeigt ihren Graphen $G_f$ .

a) Begründen Sie, dass die Gerade mit der Gleichung $y = 1$ waagrechte Asymptote von $G_f$ ist. Zeigen Sie rechnerisch, dass $f$ streng monoton abnehmend ist.

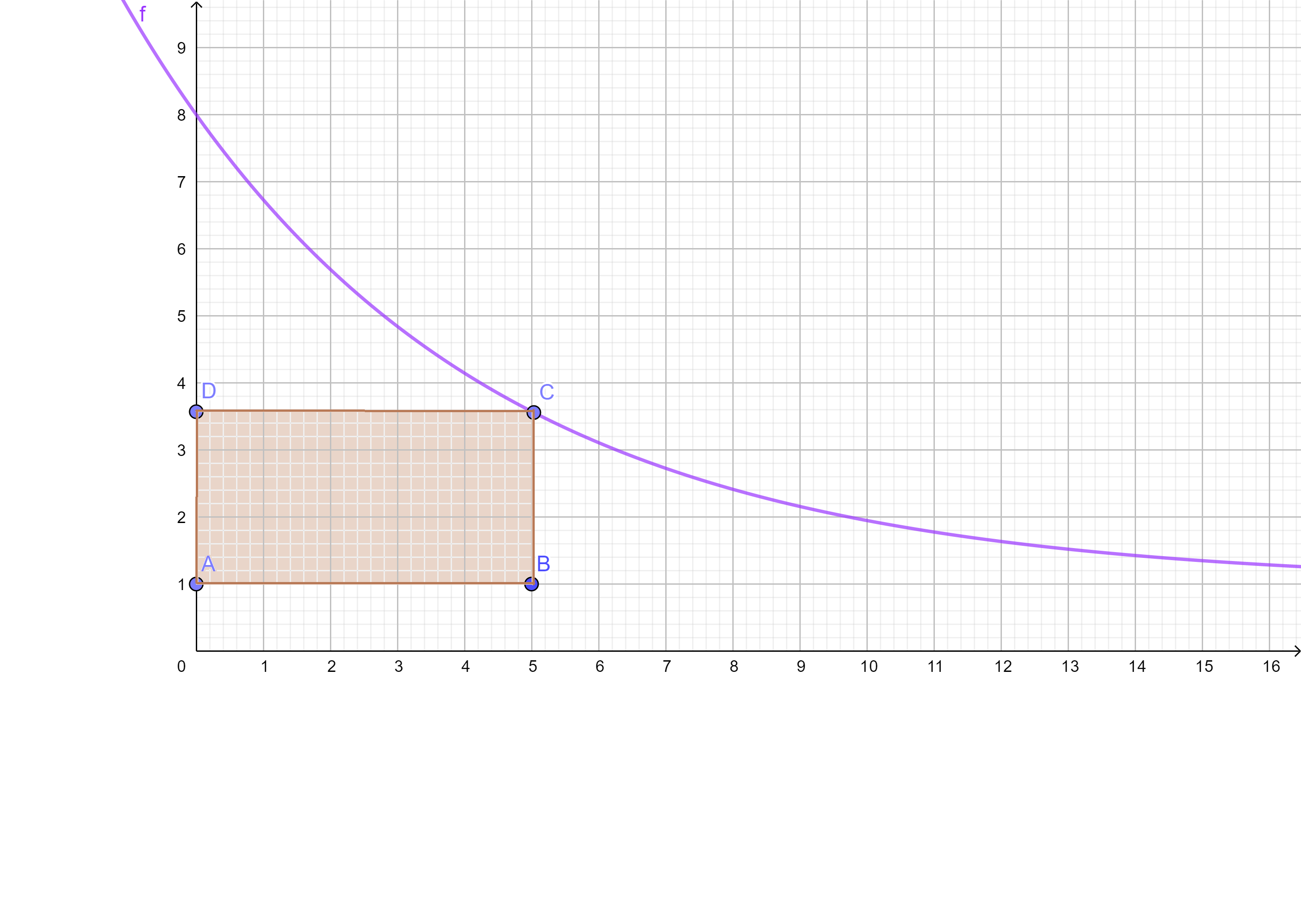
Für jeden Wert $s>0$ legen die Punkte $(0|1)$ , $(s|1)$ , $(s| f (s) )$ und $(0|f (s) )$ ein Rechteck mit dem Flächeninhalt $R(s)$ fest.

b) Zeichnen Sie dieses Rechteck für $s = 5$ in die Abbildung 1 ein. Zeigen Sie, dass $R(s)$ für einen bestimmten Wert von $s$ maximal ist, und geben Sie den Wert von $s$ an.

(zur Kontrolle: $R(s) = 7s \cdot e^{-0{,}2s}$ )

c) Berechnen Sie den Inhalt des Flächenstücks, das von $G_f$ , der y-Achse sowie den Geraden mit den Gleichungen $y = 1$ und $x=5$ begrenzt wird. Einen Teil dieses Flächenstücks nimmt das zu $s = 5$ gehörige Rechteck ein. Bestimmen Sie den prozentualen Anteil des Flächeninhalts dieses Rechtecks am Inhalt des Flächenstücks.

Teilaufgabe a)

Die e-Funktion $e_1(x)=e^x$ hat die x-Achse als waagrechte Asymptote. Da $e_2(x)=e^{-x}$ sich aus $e_1(x)$ durch Spiegelung an der y-Achse ergibt, ist die x-Achse ebenfalls eine waagrechte Asymptote von $e_2(x)$ .

Der Graph $G_{e_2}$ ergibt sich aus dem Graph $G_{e_1}$ durch Spiegelung an der y-Achse.

Also gilt: $\lim\limits_{x\to\infty}e^{-x}$ =0 und $\lim\limits_{x\to\infty}(1+7\cdot e^{-{0{,}2\cdot x}})=1$

Die Funktion $f$ ist streng monoton fallend, wenn $f'(x)<0$ für alle $x>0$

\displaystyle f'(x)=7\cdot(-0{,}2)\cdot e^{-0{,}2\cdot x}=-1{,}4\cdot e^{-0{,}2\cdot x}<0

Da $e^{-0{,}2\cdot x}>0$ , ist also $-1{,}4\cdot e^{-0{,}2\cdot x}<0$ . Somit ist $f$ streng monoton fallend.

Teilaufgabe b)

Bei dieser Aufgabe gehst du in zwei Schritten vor:

Zuerst berechnest du die Fläche des Rechtecks R(s) in Abhängigkeit von $s$ .
Dann berechnest du mithilfe der ersten Ableitung, wann R(s) maximal wird.

Das Rechteck mit den gegebenen Punkten hat die Länge $s$ und die Höhe

\displaystyle f'(x)=7\cdot(-0{,}2)\cdot e^{-0{,}2\cdot x}=-1{,}4\cdot e^{-0{,}2\cdot x}<0

Damit gilt für den Flächeninhalt:

\displaystyle f'(x)=7\cdot(-0{,}2)\cdot e^{-0{,}2\cdot x}=-1{,}4\cdot e^{-0{,}2\cdot x}<0

Dieser Wert wird maximal für den Wert von $s$ , wenn $R'(s)=0$ und an der Stelle $s$ einen Vorzeichenwechsel von $+$ nach $-$ hat.

\displaystyle f'(x)=7\cdot(-0{,}2)\cdot e^{-0{,}2\cdot x}=-1{,}4\cdot e^{-0{,}2\cdot x}<0

Berechne nun die Nullstelle von R(s):

$\displaystyle R'\left(s\right)$	$=$	$\displaystyle 0$
	↓	Setze R'(s) ein
$\displaystyle 1-0{,}2\ \cdot s$	$=$	$\displaystyle 0$	$\displaystyle -1$
$\displaystyle -0{,}2\cdot s$	$=$	$\displaystyle -1$	$\displaystyle \cdot\left(-5\right)$
$\displaystyle s$	$=$	$\displaystyle 5$

Da der Faktor $7\cdot e^{-0{,}2\cdot s}$ immer größer als 0 ist, wird das Vorzeichen von $R'(s)$ bestimmt von dem zweiten Faktor $1-\frac{1}{5}\cdot s$

Der zweite Faktor ist eine fallende Gerade mit dem y-Achsenabschnitt 1 und der Nullstelle $s=5$ .

Also ist $R'(s)>0$ für $0<s<5$ : $R$ wachsend.

Und $R'(s)<0$ für $5<s<\infty$ : $R$ fallend.

Damit wird der Inhalt des Rechteckes für $s=5$ maximal. Es gilt:

\displaystyle f'(x)=7\cdot(-0{,}2)\cdot e^{-0{,}2\cdot x}=-1{,}4\cdot e^{-0{,}2\cdot x}<0

Teilaufgabe c)

Für den Inhalt des vor beschriebenen Flächenstücks gilt:

$\displaystyle A$	$=$	$\displaystyle \int_0^5(f(x)-1)\,dx$	$\displaystyle$
	↓	Setze f(x) ein
	$=$	$\displaystyle \int_0^5(1+7\cdot e^{-0{,}2x}-1)\,dx$
	↓	Vereinfache
	$=$	$\displaystyle \int_0^57\cdot e^{-0{,}2x}dx\$
	↓	Ziehe die 7 als Skalar vor das Integral
	$=$	$\displaystyle 7\int_0^5e^{-\frac{1}{5}x}dx$
	↓	Integriere
	$=$	$\displaystyle 7\cdot(-5)[e^{-\frac{1}{5}x}]_0^5$
	↓	Werte an den Grenzen aus
	$=$	$\displaystyle -35\cdot(e^{-1}-e^0)=35-\frac{35}{e} \ \text{FE}$

Damit gilt für den Anteil des Flächenstücks des Rechtecks am Inhalt des Flächenstücks:

\displaystyle f'(x)=7\cdot(-0{,}2)\cdot e^{-0{,}2\cdot x}=-1{,}4\cdot e^{-0{,}2\cdot x}<0

Also ist der prozentuale Anteil gerade 58 %.

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.

2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
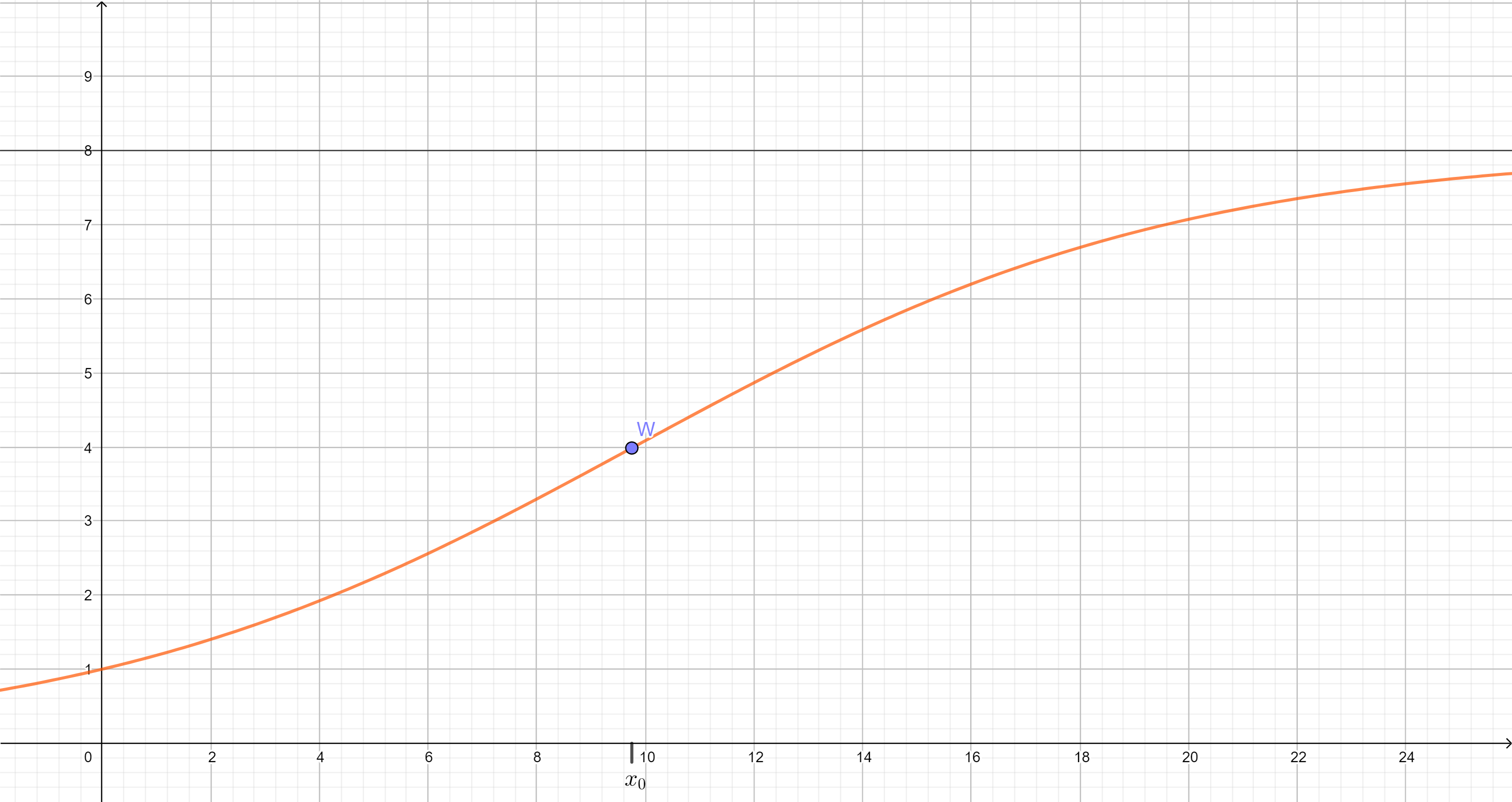
Die in $\R^+_0$ definierte Funktion $A: x \mapsto \frac{8}{f(x)}$ beschreibt modellhaft die zeitliche Entwicklung des Flächeninhalts eines Algenteppichs am Südufer eines Sees. Dabei ist $x$ die seit Beobachtungsbeginn vergangene Zeit in Tagen und $A(x)$ der Flächeninhalt in Quadratmetern.
1. Bestimmen Sie $A(0)$ sowie $\lim\limits_{x \to +\infty} A(x)$ und geben Sie jeweils die Bedeutung des Ergebnisses im Sachzusammenhang an. Begründen Sie mithilfe des Monotonieverhaltens der Funktion $f$ , der Flächeninhalt des Algenteppichs im Laufe der Zeit ständig zunimmt.
  
  $A\left(x\right)=\frac{8}{1+7\cdot e^{-\frac{x}{5}}}$
  $A\left(0\right)=\frac{8}{1+7\cdot e^{-\frac{0}{5}}}=\frac{8}{1+7\cdot1}=\frac{8}{8}=1\ FE$
  $\lim_{x\ \to\ \infty}A\left(x\right)=\frac{8}{1+7\cdot\lim_{x\ \to\infty}e^{-\frac{x}{5}}}=\frac{8}{1+0}=8FE$
  Das Monotonieverhalten zeigt man mit der 1.Ableitung von $A\left(x\right)$
  $A'\left(x\right)=8\cdot\frac{\left(-7\cdot e^{-\frac{x}{5}}\cdot\left(-\frac{1}{5}\right)\right)}{\left(1+7\cdot e^{-\frac{x}{5}}\right)^2}$
  $A'\left(x\right)=\frac{56}{5}\cdot\frac{e^{-\frac{x}{5}}}{\left(1+7\cdot e^{-\frac{x}{5}}\right)^2}>0\Rightarrow A\ streng\ monoton\ wachsend._{ }$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Bestimmen Sie denjenigen Wert $x_0$ , für den $A(x_0) = 4$ gilt, und interpretieren Sie Ihr Ergebnis im Sachzusammenhang.
  (zur Kontrolle: $x_0 \approx 9{,}7$ )
  
  Bestimme den Wert für $x_0$ , für den $A\left(x_0\right)=4$ .
  $\frac{8}{1+7\cdot e^{-\frac{x}{5}}}=4\Leftrightarrow\ 1+7\cdot e^{-\frac{x}{5}}=2\Leftrightarrow\ 7\cdot e^{-\frac{x}{5}}=1\$
  $\Leftrightarrow\text{e}^{-\frac{x}{5}}=\frac{1}{7}\Leftrightarrow\ -\frac{x}{5}=\ln\left(\frac{1}{7}\right)\Leftrightarrow\ _{ }$
  $-\frac{x}{5}=\ln\left(1\right)-\ln\left(7\right)\Leftrightarrow\ -\frac{x}{5}=-\ln\left(7\right)\Leftrightarrow$
  $x=5\cdot\ln\left(7\right)\approx9{,}7$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Bestimmen Sie die momentane Änderungsrate des Flächeninhalts des Algenteppichs zu Beobachtungsbeginn.
  
  Bestimme $A'\left(0\right)$
  $A'\left(0\right)=\frac{56}{5}\cdot\frac{1}{\left(1+7\right)^2}=\frac{7\cdot8}{5\cdot8\cdot8}=\frac{7}{40}=0{,}175$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. Nur zu dem Zeitpunkt, der im Modell durch $x_0$ (vgl. Aufgabe 2b) beschrieben wird, nimmt die momentane Änderungsrate des Flächeninhalts des Algenteppichs ihren größten Wert an. Geben Sie eine besondere Eigenschaft des Graphen von $A$ im Punkt $(x_0| A (x_0) )$ an, die sich daraus folgern lässt, und begründen Sie ihre Angabe.
  
  Zum Zeitpunkt $x_0=0{,}97$ ist die momentan Änderungsrate maximal. Somit wächst $A'\left(x\right)$ für $x<x_0$ und fällt $A'\left(x\right)$ für $x>x_0$ .Somit hat die 2. Ableitung von $A\left(x\right)$ , nämlich $A''\left(x\right)\$ an der Stelle $x=x_0$ eine Nullstelle.
  $A''\left(x\right)<0\ für\ x<x_0$ ⇒ A rechtsgekrümmt.
  $A''\left(x\right)>0\ für\ x>x_0\Rightarrow$ A linksgekrümmt.
  Insgesamt hat A an der Stelle $W\left(x_0;4\right)$ einen Wendepunkt.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
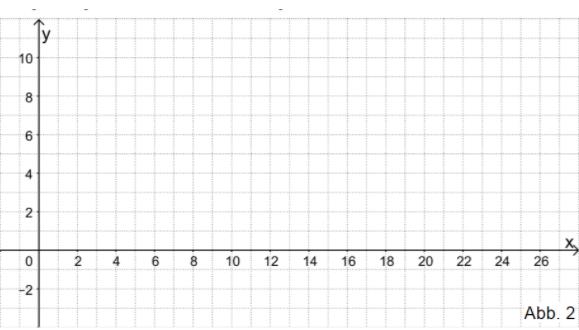
5. Skizzieren Sie den Graphen der Funktion $A$ unter Verwendung der bisherigen Ergebnisse in der Abbildung 2.
  
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
6. Um die zeitliche Entwicklung des Flächeninhalts eines Algenteppichs am Nordufer des Sees zu beschreiben, wird im Term $A (x)$ die im Exponenten zur Basis e enthaltene Zahl $-0, 2$ durch eine kleinere Zahl ersetzt. Vergleichen Sie den Algenteppich am Nordufer mit dem am Südufer
  • hinsichtlich der durch $A (0)$ und $\lim\limits_{x \to +\infty} A(x)$ beschriebenen Eigenschaften (vgl.
  Aufgabe 2a).
  • hinsichtlich der momentanen Änderungsrate des Flächeninhalts zu
  Beobachtungsbeginn (vgl. Aufgabe 2c).
  Skizzieren Sie – ausgehend von diesem Vergleich – in der Abbildung 2 den Graphen einer Funktion, die eine mögliche zeitliche Entwicklung des Flächeninhalts des Algenteppichs am Nordufer beschreibt.
  
  Im Term für $A\left(x\right)$ wird die Zahl $-0{,}2=-\frac{1}{5}$ durch eine kleinere Zahl ersetzt. Der Nenner 5 soll hier durch a ersetzt werden,
  $-\frac{1}{5}>-\frac{1}{a}\Leftrightarrow\ \frac{1}{5}<\frac{1}{a}\Leftrightarrow\text{a}<5.$
  $A_5\left(0\right)=\frac{8}{1+7\cdot e^{-\frac{0}{5}}}=1FE$
  $A_a\left(0\right)=\frac{8}{1+7\cdot e^{-\frac{0}{a}}}=1\ FE$ unabhängig von a.
  da $\lim_{x\to\ \infty\ }e^{-x}=0$ ist auch der Grenzwert von $A\left(x\right)$ für unbegrenzt wachsendes x unabhängig von der Wahl von a.
  Somit: $\lim_{x\ \to\infty\ }A\left(x\right)=8 FE$
  $A'_a\left(x\right)=8\cdot\frac{\left(-7\cdot e^{-\frac{x}{a}}\cdot\left(-\frac{1}{a}\right)\right)}{\left(1+7\cdot e^{-\frac{x}{a}}\right)^2}=8\cdot7\cdot\frac{\left(\frac{1}{a}\cdot e^{-\frac{x}{a}}\right)}{\left(1+7\cdot e^{-\frac{x}{a}}\right)^2} $
  Somit $A'_a\left(0\right)=56\cdot\frac{\left(\frac{1}{a}\cdot1\right)}{\left(1+7\cdot1\right)^2}=8\cdot7\cdot\frac{1}{a\cdot8\cdot8}=\frac{7}{8a}$
  Da, wie oben angegeben $0<a<5$ wird der Nenner $8⋅a<40$ und somit der Quotient $A'_a\left(0\right)$ größer als $A_5'\left(0\right)$ . Somit $A'_5\left(0\right)<A'_a(0)$ . Das bedeutet, dass der Algenteppich zu Beginn der Beobachtung schneller wächst, wenn man die Zahl $-0{,}2=-\frac{1}{5}$ durch eine kleinere Zahl ersetzt.
  Es ist auch interessant, zu fragen, ob die Lage des Wendepunktes W sich durch Änderung von a verschiebt.
  Dazu betrachtet man die 2. Ableitung von $A_a\left(x\right).$
  $A_a\left(x\right)=\frac{8}{1+7\cdot e^{-\frac{x}{a}}}$
  $A'_a\left(x\right)=8\cdot\frac{\left(-7\cdot e^{-\frac{x}{a}}\cdot\left(-\frac{1}{a}\right)\right)}{\left(1+7\cdot e^{-\frac{x}{a}}\right)^2}=8\cdot7\cdot\frac{\left(\frac{1}{a}\cdot e^{-\frac{x}{a}}\right)}{\left(1+7\cdot e^{-\frac{x}{a}}\right)^2}$
  $A''_a\left(x\right)=\frac{56}{a}\cdot\frac{\left(e^{-\frac{x}{a}}\cdot\left(-\frac{1}{a}\right)\right)\cdot\left(1+7e^{-\frac{x}{a}}\right)^2-e^{-\frac{x}{a}}\cdot2\left(1+7e^{-\frac{x}{a}}\right)\cdot\left(-\frac{7}{a}e^{-\frac{x}{a}}\right)}{\left(1+7\cdot e^{-\frac{x}{a}}\right)^4}$
  $A''_a\left(x\right)=\frac{56}{a}\cdot e^{-\frac{x}{a}}\cdot\frac{\left(-\frac{1}{a}\cdot\left(1+7e^{-\frac{x}{a}}\right)+2\cdot\frac{7}{a}\cdot e^{-\frac{x}{a}}\right)}{\left(1+7e^{-\frac{x}{5}}\right)^3}$
  $A''_a\left(x\right)=\frac{56\cdot e^{-\frac{x}{a}}}{a}\cdot\frac{\left(-\frac{1}{a}-\frac{7}{a}e^{-\frac{x}{a}}+\frac{\left(2\cdot7\right)}{a}\cdot e^{-\frac{x}{a}}\right)}{\left(1+7e^{-\frac{x}{a}}\right)^3}$
  $A''_a\left(x\right)=\frac{56\cdot e^{-\frac{x}{a}}}{a}\cdot\frac{-1+7\cdot e^{-\frac{x}{a}}}{a\cdot\left(1+7e^{-\frac{x}{a}}\right)^3}$
  $A_a''\left(x\right)=0\Leftrightarrow\ -1+7\cdot e^{-\frac{x}{a}}=0\Leftrightarrow\ 7e^{-\frac{x}{a}}=1$
  $A_a''\left(x\right)=0\Leftrightarrow\text{e}^{-\frac{x}{a}}=\frac{1}{7}\Leftrightarrow\ -\frac{x}{a}=\ln\left(\frac{1}{7}\right)\Leftrightarrow\text{-x}=a\cdot\ln\left(\frac{1}{7}\right)\Leftrightarrow\text{x}=a\cdot\ln\left(7\right)$
  $y_W=\frac{8}{1+7\cdot e^{-a\cdot\frac{\ln\left(7\right)}{a}}}=\frac{8}{1+7\cdot e^{-\ln\left(7\right)}}=\frac{8}{1+7\cdot\frac{1}{7}}=\frac{8}{2}=4$
  Somit verschiebt sich der Wendepunkt $W_a\left(a\cdot\ln\left(7\right);4\right)$ auf der Geraden $y=4$ mit veränderlichem a.
  $$ $$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?