Aufgabe A1
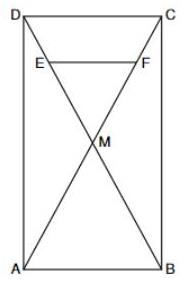
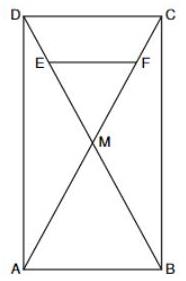
Die Skizze zeigt das Rechteck mit den Diagonalen und , den Diagonalenschnittpunkt und die Strecke .
Es gilt: ; ; ; ;
; .
Berechnen Sie den prozentualen Anteil des Flächeninhalts des Dreiecks am Flächeninhalt des Rechtecks .
Runden Sie auf zwei Stellen nach dem Komma. (4 P)
Zwischenergebnisse: ;