Nachtermin Teil A
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
- 1
Aufgabe A1
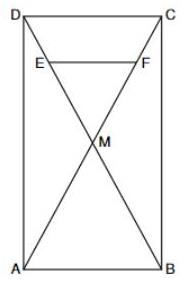
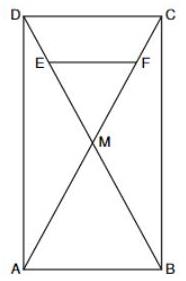
Die Skizze zeigt das Rechteck mit den Diagonalen und , den Diagonalenschnittpunkt und die Strecke .
Es gilt: ; ; ; ;
; .
Berechnen Sie den prozentualen Anteil des Flächeninhalts des Dreiecks am Flächeninhalt des Rechtecks .
Runden Sie auf zwei Stellen nach dem Komma. (4 P)
Zwischenergebnisse: ;
- 2
Aufgabe A2
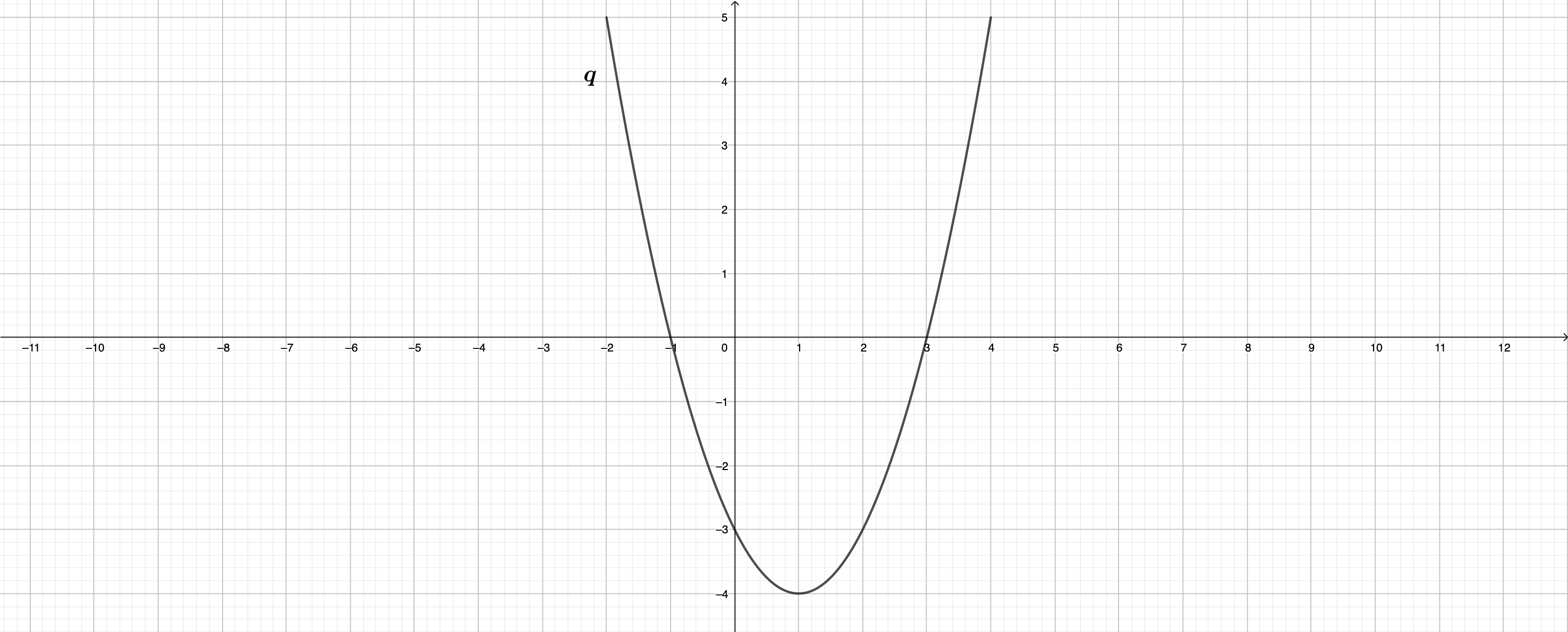
Die Parabel hat die Gleichung . x . Die Parabel ist eine nach oben geöffnete Normalparabel mit dem Scheitelpunkt .
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
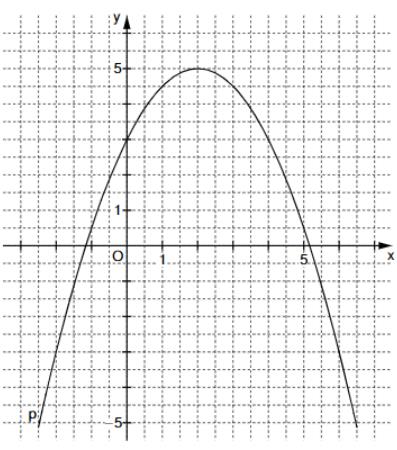
Zeichnen Sie die Parabel für in das Koordinatensystem zu 2) ein und zeige rechnerisch, dass die Gleichung x hat. (3 P)
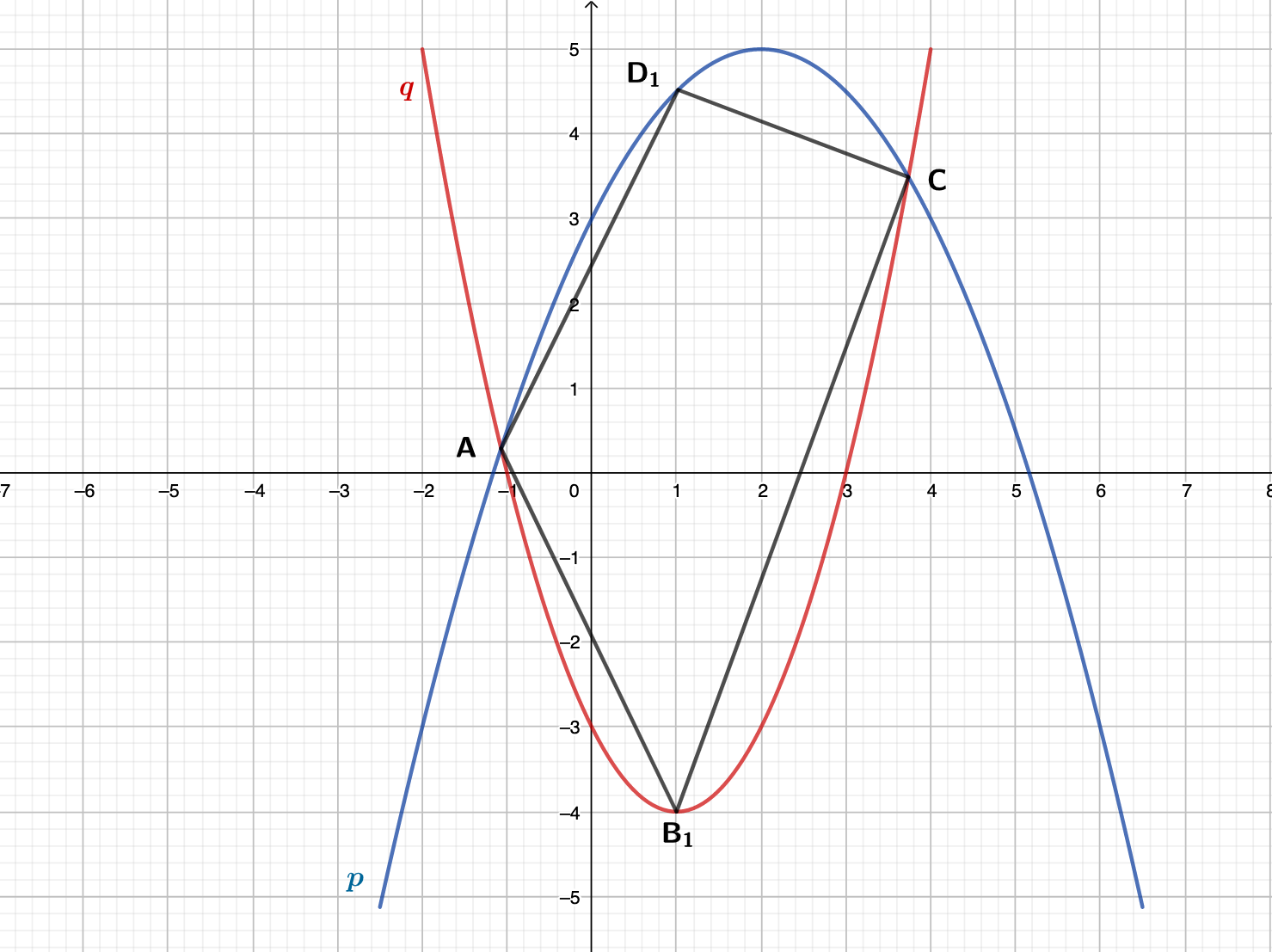
Berechnen Sie die Koordinaten der Schnittpunkte und der Parabeln und , wobei gelten soll: (3 P)
Teilergebnis: ;
Punkte auf der Parabel und Punkte
auf der Parabel haben dieselbe Abszisse . Sie sind zusammen mit den Punkten A und C für Eckpunkte von Vierecken . Zeichnen Sie das Viereck für in das Koordinatensystem zu 2) ein. (1 P)
Ist das Viereck ein Trapez mit den Grundseiten und ?
Begründen Sie Ihre Entscheidung rechnerisch. (4 P)
- 3
Aufgabe A3
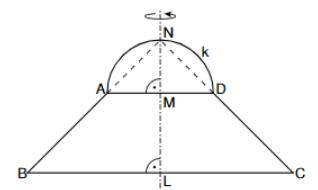
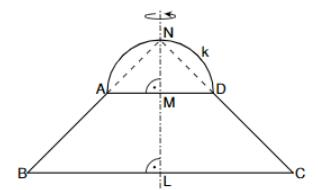
Die Skizze zeigt eine zur Geraden achsensymmetrische Figur, die aus dem gleichschenkligen Trapez und dem Halbkreis mit dem Mittelpunkt und dem Radius besteht.
Es gilt: ; ; ; ; .
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
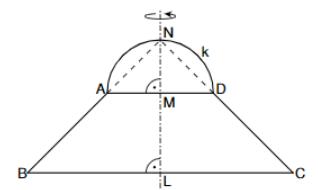
Begründen Sie, dass gilt: .
Bestimmen Sie sodann den Radius des Halbkreises . (3 P)
Teilergebnis:
Durch Rotation der Figur aus der Aufgabenstellung um die Achse entsteht ein Rotationskörper. Berechnen Sie dessen Volumen. (3 P)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?