Aufgabe A3
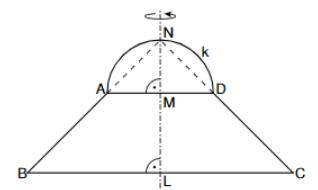
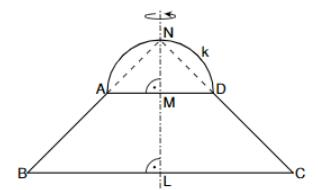
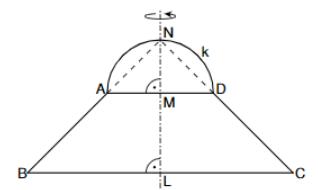
Die Skizze zeigt eine zur Geraden achsensymmetrische Figur, die aus dem gleichschenkligen Trapez und dem Halbkreis mit dem Mittelpunkt und dem Radius besteht.
Es gilt: ; ; ; ; .
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
Begründen Sie, dass gilt: .
Bestimmen Sie sodann den Radius des Halbkreises . (3 P)
Teilergebnis:
Durch Rotation der Figur aus der Aufgabenstellung um die Achse entsteht ein Rotationskörper. Berechnen Sie dessen Volumen. (3 P)