Aufgabe A2
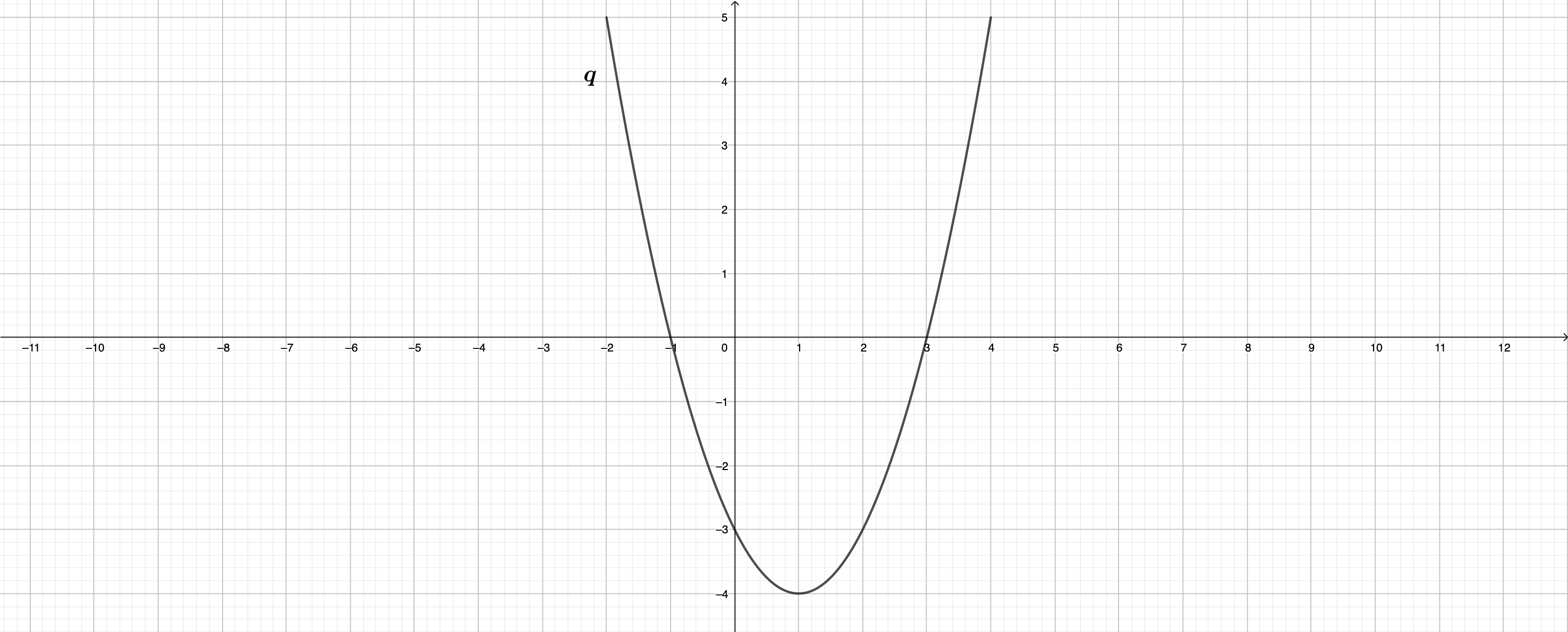
Die Parabel hat die Gleichung . x . Die Parabel ist eine nach oben geöffnete Normalparabel mit dem Scheitelpunkt .
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
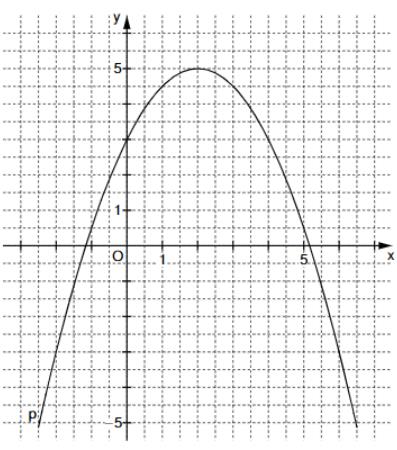
Zeichnen Sie die Parabel für in das Koordinatensystem zu 2) ein und zeige rechnerisch, dass die Gleichung x hat. (3 P)
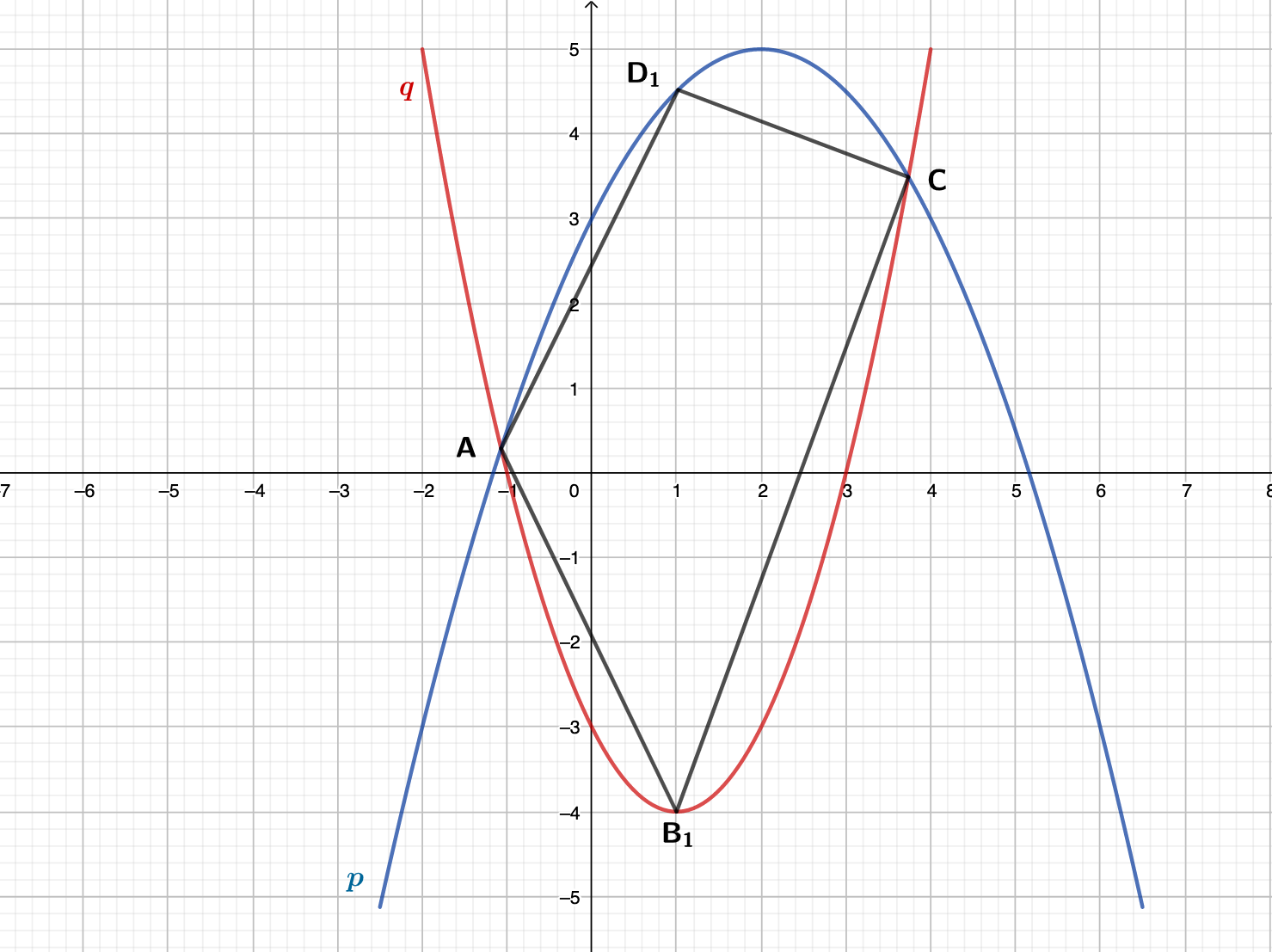
Berechnen Sie die Koordinaten der Schnittpunkte und der Parabeln und , wobei gelten soll: (3 P)
Teilergebnis: ;
Punkte auf der Parabel und Punkte
auf der Parabel haben dieselbe Abszisse . Sie sind zusammen mit den Punkten A und C für Eckpunkte von Vierecken . Zeichnen Sie das Viereck für in das Koordinatensystem zu 2) ein. (1 P)
Ist das Viereck ein Trapez mit den Grundseiten und ?
Begründen Sie Ihre Entscheidung rechnerisch. (4 P)