Wie wertet man ein Diagramm aus?

Im Folgenden werden zuerst verschiedene Typen von Diagrammen vorgestellt und erklärt, wieso Manipulation bei Diagrammen ein großes Problem ist. Erst wird Schritt für Schritt erläutert, wie man ein Diagramm auswertet.

Typen von Diagrammen

Für das Auswerten von Diagrammen muss man den Diagrammtyp immer im Hinterkopf behalten. Eine andere Darstellung kann die Daten in völlig anderem Licht erscheinen lassen!

Verschiedene Typen von Diagrammen eigenen sich zur Darstellung verschiedener Schwerpunkte. Die am häufigsten verwendeten Typen sind dabei das Liniendiagramm, das Säulendiagramm und das Kreisdiagramm.

Drei wichtige Typen von Diagrammen:

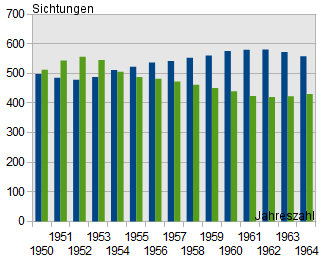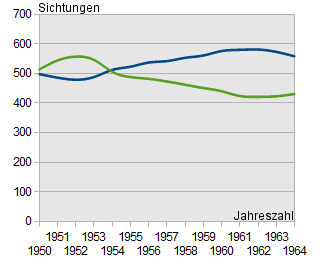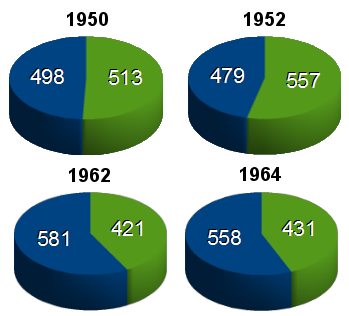Manipulation von Diagrammen

Diagramme lassen sich leicht manipulieren, um Daten anders erscheinen zu lassen, als sie sind. Dazu reicht es oft schon, einen anderen Ausschnitt der Datenwerte oder eine andere Form der Darstellung zu wählen.

Im folgenden Beispiel sind dreimal dieselben Daten dargestellt. Lediglich der Ausschnitt der x- und y-Achse wurde verändert. Dennoch kommt man beim oberflächlichen Betrachten des Diagramms schnell zu sehr unterschiedlichen Schlüssen!

Daher gilt der scherzhafte Merksatz: "Vertraue keinem Diagramm, dass du nicht selbst gefälscht hast"

Drei Beispiele für Manipulation:

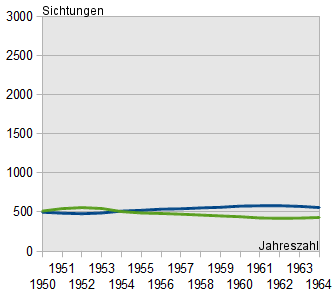
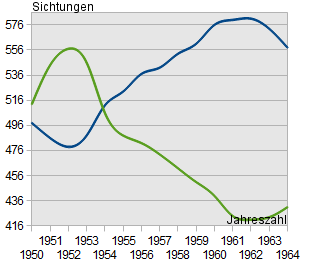
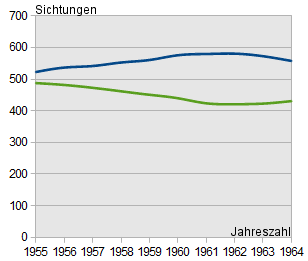
"In den letzten Jahren gab es kaum Veränderungen. Es besteht also kein Anlass zur Sorge."

"In den letzten Jahren gab es drastische Veränderungen! Wir müssen dringend etwas unternehmen!"

"In den letzten Jahren gab es immer mehr Falken als Mäuse. Das wird auch so bleiben"

Auswerten von Diagrammen

Schritt 1: Grundlagen ablesen

Zuerst achtet man auf die Beschriftung und die Legende des Diagramms. Was stellt das Diagramm überhaupt dar?

In unserem Beispiel…

• x-Achse: Es handelt sich um die Jahreszahl des Sommers, in dem die Tiere gesichtet wurden.

• y-Achse: Es handelt sich um die Anzahl der Sichtungen

• Blaue Linie: Die Anzahl der gesichteten Turmfalken

• Grüne Linie: Die Anzahl der gesichteten Feldmäuse

Das Diagramm stellt also dar, wie viele Turmfalken und Feldmäuse im Verlauf der Jahre gesichtet worden sind.

Schritt 2: Wichtige Punkte ablesen

Zuerst müssen die wichtigsten Punkte abgelesen werden. Wichtige Punkte sind etwa Hoch-, Tief-, Wende- oder Schnittpunkte.

In unserem Beispiel…

• 1952: Ein Hochpunkt der Mäuse- und ein Tiefpunkt der Falkenlinie. Ein Wendepunkt für beide Linien.

• 1954: Ein Schnittpunkt zwischen der Falken- und Mäuselinie

• 1962: Ein Tiefpunkt der Mäuse- und ein Hochpunkt der Falkenlinie. Ein Wendepunkt für beide Linien.

Schritt 3: Trends bestimmen

Nun gilt es, alle wichtigen Trends zu bestimmen.

In unserem Beispiel…

Sichtungen an Turmfalken

• Ab 1950 fallen sie leicht ab

• Ab 1952 steigen sie stetig an

• Ab 1962 fallen sie wieder leicht ab

Sichtungen an Feldmäusen

• Ab 1950 steigen sie stark an

• Ab 1952 fallen sie stark ab

• Ab 1954 fallen sie deutlich langsamer

• Ab 1962 steigen sie wieder leicht an

Schritt 4: Trends vergleichen

Die einzelnen Trends lassen sich nun vergleichen, um Unterschiede und Zusammenhänge festzustellen.

Gibt es gemeinsame Tendenzen? Ist ein Muster zu erkennen?

In unserem Beispiel…

• Wenn es viele Mäusesichtungen gibt, gibt es wenige Falkensichtungen.

• Wenn es viele Falkensichtungen gibt, gibt es wenige Mäusesichtungen.

Schritt 5: Trends deuten

Zuletzt können anhand der Vergleiche biologische Hyphothesen aufgestellt werden, wie die Daten zusammenhängen. Die Hypothesen müssen dann hinterfragt und bewertet werden.

In unserem Beispiel…

A) "Die Mäuse fressen die Falken. Daher gibt es immer dann viele Falken, wenn es weniger Mäuse gibt."

• Nach dem Diagramm kann dieser Zusammenhang sein. Hier muss man aber die Theorie beachten: Es ist bekannt, dass Mäuse keine Falken fressen!

B) "Die Falken jagen die Mäuse. Darum kann es nur dann viele Mäuse geben, wenn es wenige Falken gibt."

• Mäuse sind typische Beutetiere für die Falken. Die Hypothese könnte stimmen.

C) "Die Mäuse verstecken sich vor den Falken. Wenn also viele Falken unterwegs sind, kann man nur noch wenige Mäuse entdecken."

• Beutetiere schützen sich oft vor ihren Jägern, etwa durch Verstecken. Auch diese Hypothese ist also möglich.

D) "Der Zusammenhang zwischen Falken- und Mäusesichtungen ist nur ein Scheinzusammenhang. Die Anzahl der Sichtungen geht auf völlig andere Gründe zurück."

• Scheinzusammenhänge kommen sehr häufig vor. Es kann schließlich an vielen Dingen liegen, wie viele Tiere Herr Schäfer über einen Sommer hinweg entdeckt. Auch diese Hypothese kann also richtig sein.

Schlussfolgerung)

• Mit einem Diagramm lassen sich oft nur Hypothesen formulieren. Um diese Hypothesen dann zu überprüfen, sind meist Experimente notwendig.

Lerne, wie man ein Experiment plant!

Schritt 6: Verlauf vorhersagen

Aufgrund des Diagrammverlaufes und der aufgestellten Hypothesen, lassen sich Vorhersagen machen, wie der zukünftige Verlauf des Diagramms aussehen könnte.

Achtung! Diese Vorhersagen sind immer nur Spekulationen!

In unserem Beispiel…

• Zum Schluss hin, neigen sich die Linien wieder einander zu. Verlaufen die Linien wieder so weiter, kommt es erneut zu einem Schnittpunkt.

• In den folgenden Jahren könnte es wieder mehr Mäuse- als Falkensichtungen geben.