Der Kreisumfang ist die Länge der Kreislinie.
Das Formelzeichen für den Kreisumfang ist ein .
Die Kreisfläche ist die Fläche innerhalb der Kreislinie.
Im Bild ist die Kreisfläche rot markiert.
Das Formelzeichen für die Kreisfläche ist ein .
Zusammenfassung
Begriff | Formel mit dem Radius r | Formel mit dem Durchmesser d |
|---|---|---|
Kreisumfang | ||
Kreisfläche |
Bestimmung des Kreisumfangs
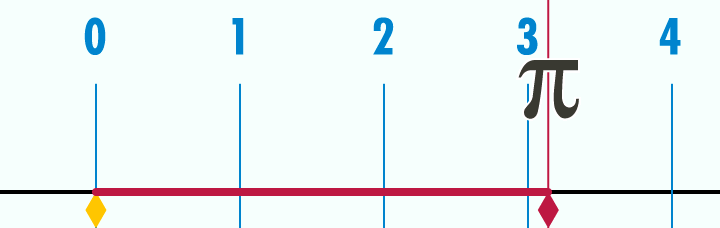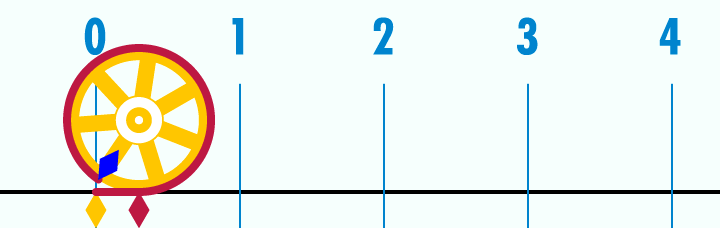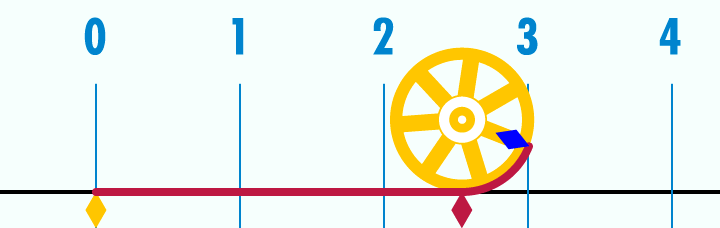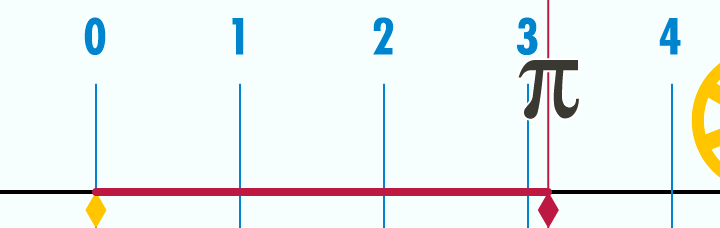
Den Kreisumfang erhältst du durch Abrollen des Kreises und Messen der abgerollten Strecke.
In der Abbildung unten siehst du, wie ein Kreis mit dem Durchmesser abgerollt wird.
Sein Umfang beträgt , also etwa .
Quelle: John Reid, Wikimedia Commons CCBY-SA 3.0
Mit diesem Vorgehen findest du folgenden Zusammenhang zwischen Durchmesser und Umfang:
Für den Zusammenhang zwischen Radius und Umfang gilt dann:
Berechnung der Kreisfläche
Berechnung mit dem Radius :
ist die Kreiszahl (Link) und hat einen Wert von ungefähr .
Das heißt: Die Kreisfläche ist etwas mehr als 3 mal so groß wie das Quadrat über dem Radius .
Berechnung mit dem Durchmesser :

Der Radius von einem Kreis beträgt
.
| ↓ | Setze den Radius ein | ||
| ↓ | Quadriere | ||
| ↓ | Gib die Rechnung in den Taschenrechner ein. Wenn dein Taschenrechner kein hat, setze ein. | ||
