Teil A - lernen mit Serlo!

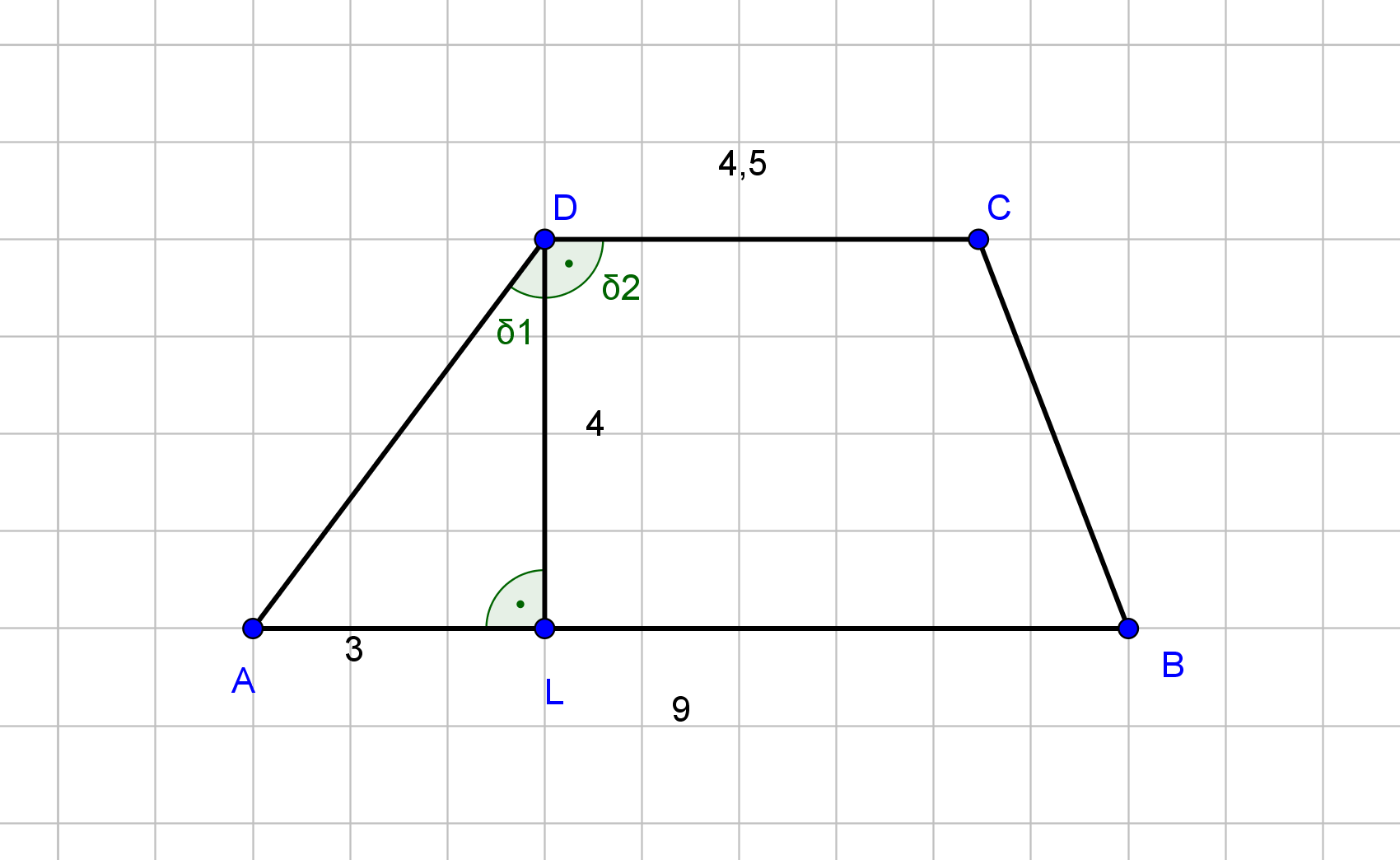
Die Zeichnung zeigt das Trapez $A B C D$ mit $[A B] ∥ [C D]$ .

Es gilt: $A B = 9 cm; C D = 4,5 cm; A L = 3 cm; D L = 4 cm$ .

Runden Sie im Folgenden auf zwei Stellen nach dem Komma.

Berechnen Sie das Maß $δ$ des Winkels $A D C$ .
°

Für diese Aufgabe benötigst Du folgendes Grundwissen: Trapez
Lösung zu a
Der Winkel $δ$ lässt sich zerlegen in zwei Teilwinkel, $δ_{1}$ und $δ_{2}$ .
$δ_{2}$ ist ein rechter Winkel, denn die Seiten $A B$ und $D C$ im Trapez $A B C D$ sind parallel und $D L$ ist als Höhe des Trapezes senkrecht auf diese beide Seiten.
$δ_{2} = 90^{\circ}$
$δ_{1}$ lässt sich mit den Trigonometrischen Funktionen im rechtwinkligen Dreieck berechnen.
Die Seite $A L$ ist die Gegenkathete zum Winkel $δ_{1}$ , die Seite $D L$ die Ankathete.
Du verwendest deshalb den Tangens:
$\tan (δ_{1}) = \frac{Gegenkathete}{Ankathete} = \frac{3}{4}$
$δ_{1} = \tan^{- 1} (\frac{3}{4})$
$δ_{1} = 36,87^{\circ}$
Setze nun die beiden Winkel zusammen.
$δ = δ_{1} + δ_{2} = 36,87^{\circ} + 90^{\circ} = 126,87^{\circ}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
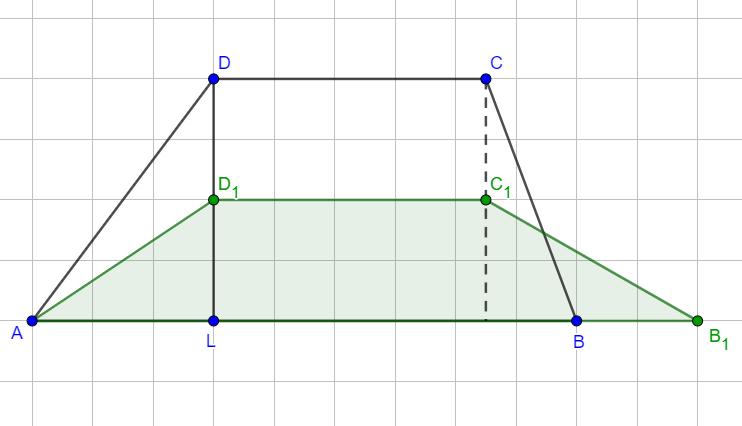
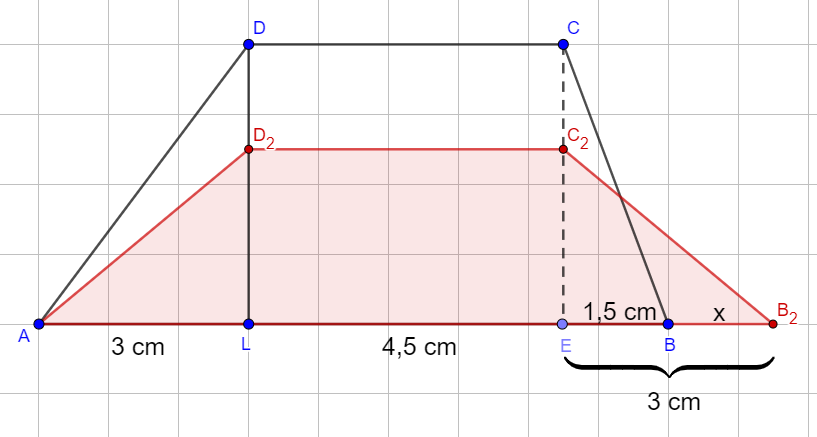
Verlängert man die Seite $[A B]$ über $B$ hinaus um $x cm$ und verkürzt gleichzeitig die Strecke $[D L]$ von $D$ aus um $x c m$ , so entstehen für $x \in ℝ; x \in] 0; 4 [$ Trapeze $A B_{n} C_{n} D_{n}$ mit $[A B_{n}] ∥ [C_{n} D_{n}]$ und $C_{n} D_{n} = 4,5 cm$ .
Zeichnen Sie das Trapez $A B_{1} C_{1} D_{1}$ für $x = 2$ in die Zeichnung in der Aufgabenstellung ein.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Trapez
Lösung zu b
Verschiebe den Punkt $B$ um $2 cm$ nach außen, von $A$ weg und den Punkt $C$ und $D$ jeweils $2 cm$ nach unten.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Geben Sie den Wert für $x$ an, für den man das gleichschenklige Trapez $A B_{2} C_{2} D_{2}$ erhält.
cm

Lösung zu c
Das gleichschenklige Trapez ist achsensymmetrisch.
Die Strecke $A L$ bleibt immer $3 cm$ , die Strecke $D C = L E$ bleibt immer $4,5 cm$ . Damit das Trapez symmetrisch wird, muss $E B_{2}$ ebenfalls $3 cm$ lang sein.
$E B = 9 cm - (3 cm + 4,5 cm) = 1,5 cm$ .
Um insgesamt die Länge $3 cm$ zu erhalten, muss also $x = 3 cm - 1,5 cm = 1,5 cm$ sein.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechnen Sie den Flächeninhalt $A$ der Trapeze $A B_{n} C_{n} D_{n}$ in Abhängigkeit von $x$ .
$[$ Ergebnis: $A (x) = (- 0,5 x^{2} - 4,75 x + 27) {cm}^{2}$ $]$

Lösung zu d
Zunächst brauchst du die allgemeine Formel für die Fläche des Trapezes:
$A_{Trapez} = \frac{a + c}{2} \cdot h$
Die Strecke $a = D C$ bleibt fest, die anderen beiden verändern sich!
$a = D C = 4,5$
Die Strecken $c = A B_{n}$ und $h = D_{n} L$ verändern sich in Abhängigkeit von x.
c wird um x cm verlängert, h um x cm verkürzt.
$c = A B + x = 9 + x$ $h = D L - x = 4 - x$
Setze alle Strecken in die Formel ein.
$\begin{array}{lcl} A_{Trapez} (x) & = & \frac{4,5 + 9 + x}{2} \cdot (4 - x) \\ = & \frac{13,5 + x}{2} \cdot (4 - x) \\ = & (6,75 + 0,5 x) (4 - x) \\ = & 27 - 6,75 x + 2 x - 0,5 x^{2} \\ = & - 0,5 x^{2} - 4,75 x + 27 \end{array}$
Es ist also $A (x) = (- 0,5 x^{2} - 4,75 x + 27) {cm}^{2}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Begründen Sie durch Rechnung, dass es unter den Trapezen $A B_{n} C_{n} D_{n}$ für $x \in] 0; 4 [$ kein Trapez mit einem Flächeninhalt von $28 {cm}^{2}$ gibt.

Lösung zu e
Die Fläche des Trapezes soll $28 {cm}^{2}$ sein, das ist der Wert der Funktion $A_{Trapez} (x)$ . Setze das Ergebnis aus Teilaufgabe d) mit 28 gleich.
$\begin{array}{rcll} 28 & = & - 0,5 x^{2} - 4,75 x + 27 & | - 28 \\ 0 & = & - 0,5 x^{2} - 4,75 x - 1 \end{array}$
Bringe die Gleichung auf die Form $a x^{2} + b x + c = 0$ , um die Mitternachtsformel anzuwenden.
$x_{1 / 2} = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$
Setze die Werte ein.
$x_{1 / 2} = \frac{4,75 \pm \sqrt{(- 4,75)^{2} - 4 \cdot (- 0,5) \cdot (- 1)}}{2 \cdot (- 0,5)}$ $x_{1} = - 9,28$ $x_{2} = - 0,22$
Beide Werte liegen nicht im Bereich $] 0; 4 [$ . Deshalb gibt es kein Trapez, das diese Vorgaben erfüllt.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇