Teil A

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Der Wertverlust verschiedener E-Bike-Modelle liegt zwischen $14$ und $33$ Prozent jährlich. Der Restwert $y$ Euro des E-Bikes "Blitz" (Neupreis $3500$ Euro) nach $x$ Jahren lässt sich näherungsweise durch die Funktion $f:~y=3500\cdot0{,}85^x$ $(\mathbb{G}=\mathbb{R}_0^+\times\mathbb{R}_0^+)$ bestimmen.
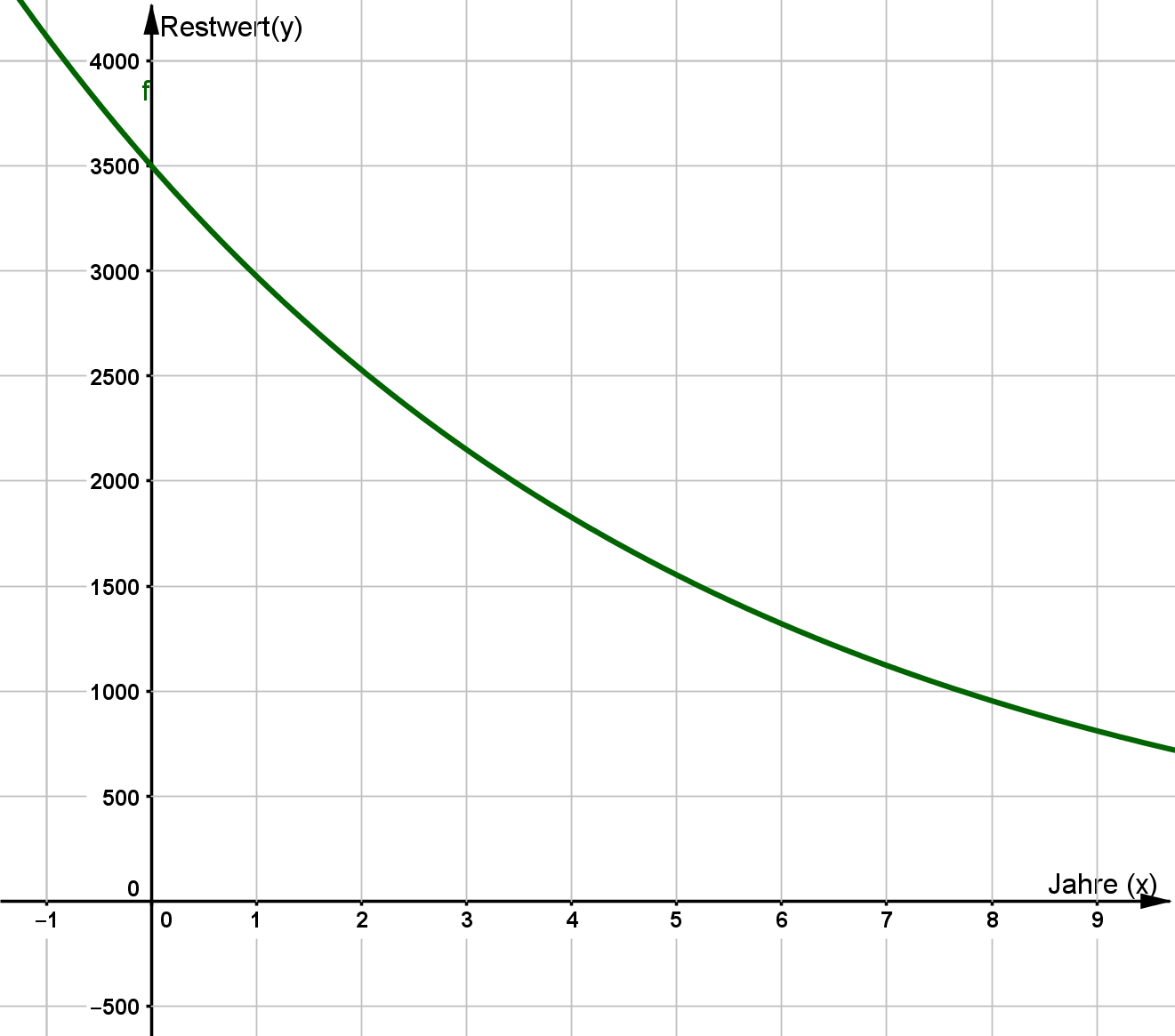
1. Ergänzen Sie die Wertetabelle auf Ganze gerundet und zeichnen Sie sodann den Graphen der Funktion $f$ in das Koordinatensystem.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentialfunktion
  Lösung zu a
  Um die Wertetabelle zu befüllen, setze die $x$ -Werte in die Funktion $f: y=3500\cdot 0{,}85^x$ ein.
  $x$
  0
  1
  2
  3
  4
  5
  6
  7
  8
  $3500\cdot0{,}85^x$
  $3500$
  $2975$
  $2529$
  $2149$
  $1827$
  $1553$
  $1320$
  $1122$
  $954$
  Übertrage nun die Werte aus der Tabelle in das Koordinatensystem:
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
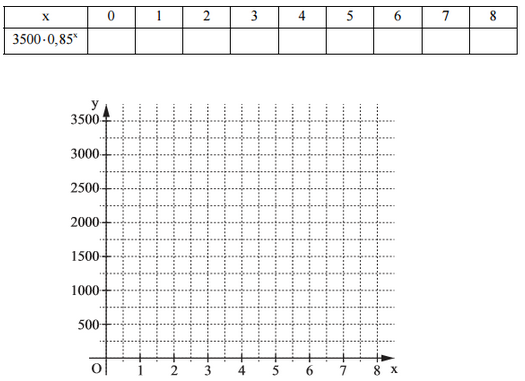
2. Berechnen Sie den Wertverlust des E-Bikes "Blitz" in Euro nach den ersten drei Jahren.
  €
  
  Lösung zu b
  Die Funktion $f$ liefert laut Angabe den Restwert des Fahrrads. Der Wertverlust ist die Differenz aus dem ursprünglichen Preis und dem Preis nach $3$ Jahren. Nimm die Werte aus der Tabelle:
  Preis im Jahr $0$ : $3500\ €$
  Preis im Jahr $3$ : $2149\ €$
  $\Rightarrow$ Wertverlust: $1351\ €$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
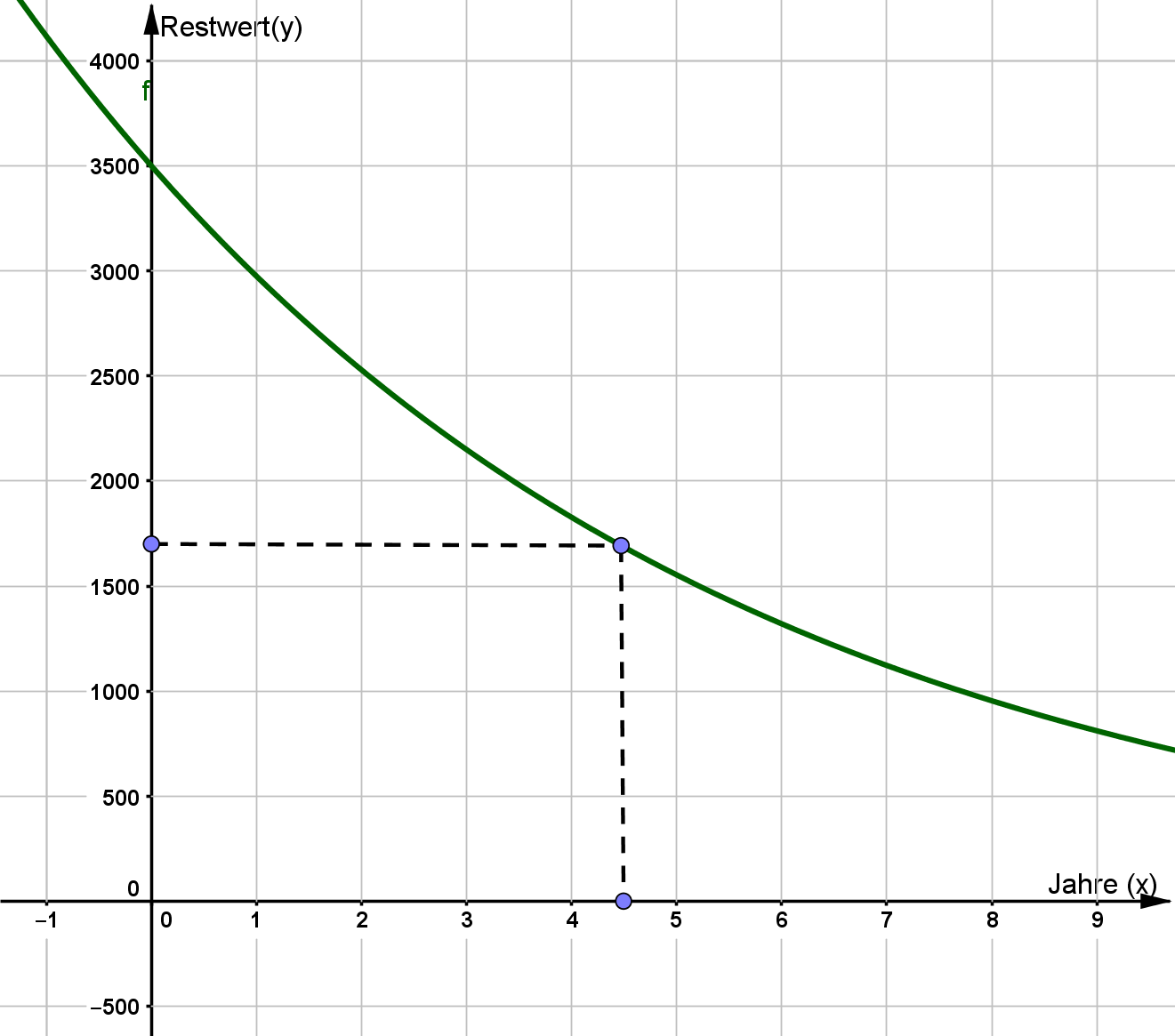
3. Ermitteln Sie mithilfe des Graphen der Funktion $f$ nach welcher Zeit sich der Wert des E-Bikes "Blitz" halbiert hat.
  Jahre
  
  Lösung zu c
  Das Fahrrad ist noch die Hälfte seines ursprünglichen Preises wert, also:
  $3500\ € : 2= 1750\ €$
  Dies ist ein $y$ -Wert. Suche den zugehörigen $x$ -Wert.
  Da der $x$ -Wert ungefähr in der Mitte zwischen $4$ und $5$ Jahren liegt, halbiert sich der Wert des Fahrrads nach ungefähr $4,5$ Jahren.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
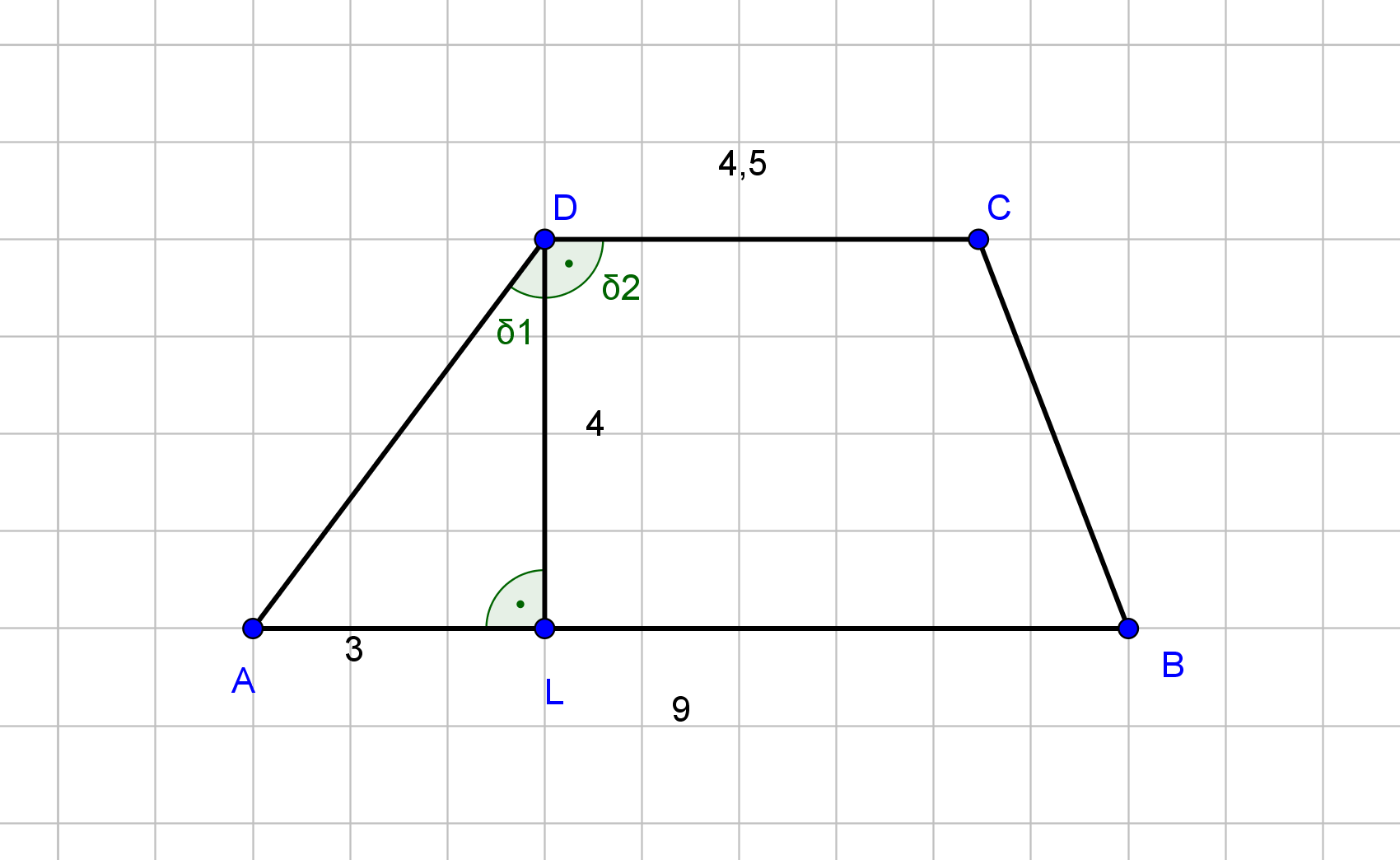
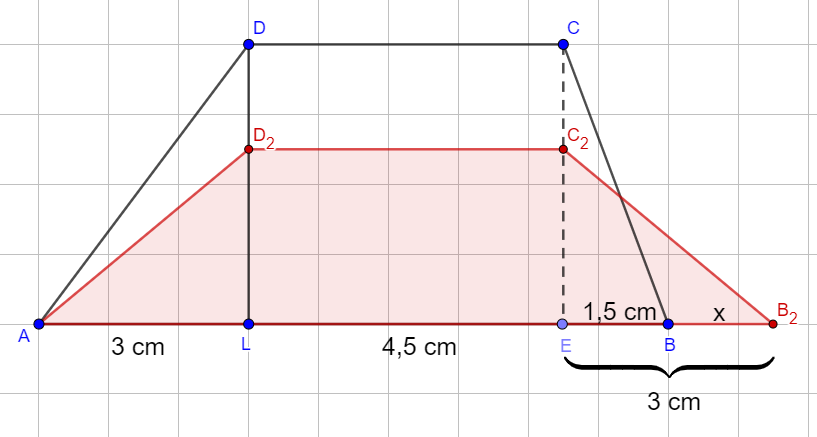
Die Zeichnung zeigt das Trapez $A B C D$ mit $[AB]~\parallel~[CD]$ .
Es gilt: $\overline{AB}=9\;\text{cm};~\overline{CD}=4{,}5\;\text{cm};~\overline{AL}=3\;\text{cm};~\overline{DL}=4\;\text{cm}$ .
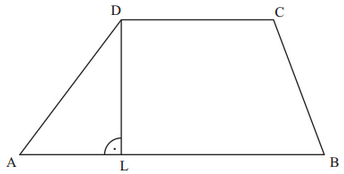
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
1. Berechnen Sie das Maß $\delta$ des Winkels $A D C$ .
  °
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Trapez
  Lösung zu a
  Der Winkel $\delta$ lässt sich zerlegen in zwei Teilwinkel, $\delta_1$ und $\delta_2$ .
  $\delta_2$ ist ein rechter Winkel, denn die Seiten $\overline{AB}$ und $\overline{DC}$ im Trapez $A B C D$ sind parallel und $\overline{DL}$ ist als Höhe des Trapezes senkrecht auf diese beide Seiten.
  $\delta_2=90^\circ$
  $\delta_1$ lässt sich mit den Trigonometrischen Funktionen im rechtwinkligen Dreieck berechnen.
  Die Seite $\overline{AL}$ ist die Gegenkathete zum Winkel $\delta_1$ , die Seite $\overline{DL}$ die Ankathete.
  Du verwendest deshalb den Tangens:
  $\tan(\delta_1)=\frac{\text{Gegenkathete}}{\text{Ankathete}}=\frac{3}{4}$
  $\delta_1=\tan^{-1}(\frac{3}{4})$
  $\delta_1= 36{,}87\ ^\circ$
  Setze nun die beiden Winkel zusammen.
  $\delta= \delta_1+\delta_2= 36{,}87\ ^\circ+90\ ^\circ= 126{,}87\ ^\circ$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
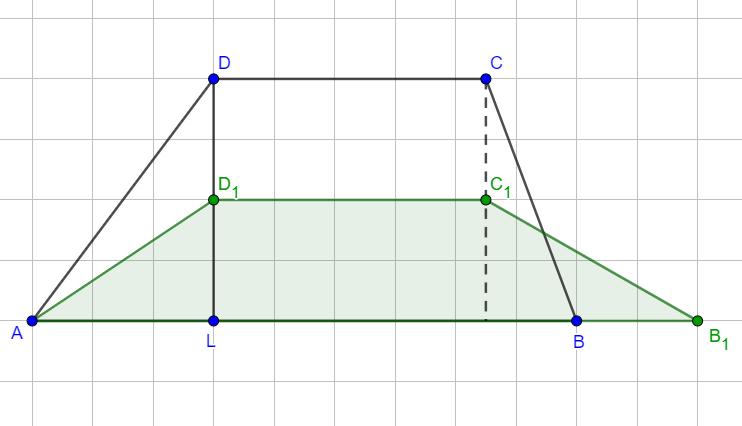
2. Verlängert man die Seite $[A B]$ über $B$ hinaus um $x\;\text{cm}$ und verkürzt gleichzeitig die Strecke $[D L]$ von $D$ aus um $x c m$ , so entstehen für $x\in\mathbb{R};~x\in\;]0;4[$ Trapeze $A B_{n} C_{n} D_{n}$ mit $[AB_n]\parallel[C_nD_n]$ und $\overline{C_nD_n}=4{,}5\;\text{cm}$ .
  Zeichnen Sie das Trapez $A B_{1} C_{1} D_{1}$ für $x = 2$ in die Zeichnung in der Aufgabenstellung ein.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Trapez
  Lösung zu b
  Verschiebe den Punkt $B$ um $2\;\text{cm}$ nach außen, von $A$ weg und den Punkt $C$ und $D$ jeweils $2\;\text{cm}$ nach unten.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Geben Sie den Wert für $x$ an, für den man das gleichschenklige Trapez $A B_{2} C_{2} D_{2}$ erhält.
  cm
  
  Lösung zu c
  Das gleichschenklige Trapez ist achsensymmetrisch.
  Die Strecke $\overline{AL}$ bleibt immer $3\;\text{cm}$ , die Strecke $\overline{DC}=\overline{LE}$ bleibt immer $4{,}5\;\text{cm}$ . Damit das Trapez symmetrisch wird, muss $\overline{EB_2}$ ebenfalls $3\;\text{cm}$ lang sein.
  $\overline{EB}\ =\ 9\ \mathrm{cm}\ -\ \left(3\ \mathrm{cm}\ +\ 4{,}5\ \mathrm{cm}\right)\ =\ 1{,}5\ \mathrm{cm}$ .
  Um insgesamt die Länge $3\;\text{cm}$ zu erhalten, muss also $x\ =\ 3\ \mathrm{cm}\ -\ 1{,}5\ \mathrm{cm}\ =1{,}5\ \mathrm{cm}$ sein.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. Berechnen Sie den Flächeninhalt $A$ der Trapeze $A B_{n} C_{n} D_{n}$ in Abhängigkeit von $x$ .
  $[$ Ergebnis: $A(x)=(-0{,}5x^2-4{,}75x+27)\;\text{cm}^2$ $]$
  
  Lösung zu d
  Zunächst brauchst du die allgemeine Formel für die Fläche des Trapezes:
  $A_{\text{Trapez}}=\frac{a+c}{2}\cdot h$
  Die Strecke $a=\overline{DC}$ bleibt fest, die anderen beiden verändern sich!
  $a=\overline{DC}=4{,}5$
  Die Strecken $c=\overline{AB_n}$ und $h=\overline{D_nL}$ verändern sich in Abhängigkeit von x.
  c wird um x cm verlängert, h um x cm verkürzt.
  $c=\overline{AB}+x= 9 +x$ $h= \overline{DL}-x= 4-x$
  Setze alle Strecken in die Formel ein.
  $\def\arraystretch{2} \begin{array}{lcl}A_{\text{Trapez}}(x) & = & \dfrac{4{,}5+9+x}{2}\cdot(4-x)\\ \\ & =& \dfrac{13{,}5 +x}{2}\cdot(4-x) \\ \\ & = &(6{,}75 +0{,}5x)(4-x)\\ &=& 27-6{,}75x+2x-0{,}5x^2\\ &=&-0{,}5x^2-4{,}75x+27\end{array}$
  Es ist also $A(x)=(-0{,}5x^2-4{,}75x+27)\;\text{cm}^2$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
5. Begründen Sie durch Rechnung, dass es unter den Trapezen $A B_{n} C_{n} D_{n}$ für $x\in]0;4[$ kein Trapez mit einem Flächeninhalt von $28\;\text{cm}^2$ gibt.
  
  Lösung zu e
  Die Fläche des Trapezes soll $28\ \mathrm{cm}^2$ sein, das ist der Wert der Funktion $A_{\text{Trapez}}(x)$ . Setze das Ergebnis aus Teilaufgabe d) mit 28 gleich.
  $\def\arraystretch{1.25} \begin{array}{rcll}28&=&-0{,}5x^2-4{,}75x+27 &|-28 \\0&=& -0{,}5x^2-4{,}75x-1\end{array}$
  Bringe die Gleichung auf die Form $a x^{2} + b x + c = 0$ , um die Mitternachtsformel anzuwenden.
  $x_{1/2}=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}$
  Setze die Werte ein.
  $x_{1/2}=\dfrac{4{,}75\pm \sqrt{(-4{,}75)^2-4\cdot (-0{,}5)\cdot (-1)}}{2\cdot (-0{,}5)}$ $x_{1}=-9{,}28$ $x_2=-0{,}22$
  Beide Werte liegen nicht im Bereich $] 0; 4 [$ . Deshalb gibt es kein Trapez, das diese Vorgaben erfüllt.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

$x$	0	1	2	3	4	5	6	7	8
$3500\cdot0{,}85^x$	$3500$	$2975$	$2529$	$2149$	$1827$	$1553$	$1320$	$1122$	$954$

Eine Schreinerei stellt Spielzeugkreisel aus Holz her. Die nebenstehende Zeichnung des Axialschnitts eines Rotationskörpers mit der Rotationsachse $B M$ dient als Vorlage für solche Spielzeugkreisel.

Es gilt: $\overline{AC}=5\;\text{cm};~\overline{BM}=4{,}5\;\text{cm};~\overline{AN}=\overline{BN};~\sphericalangle BFE=77°$

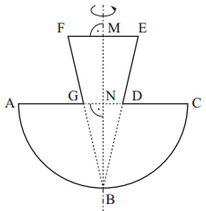
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.

Berechnen Sie die Länge der Strecke $[F M]$ und die Länge der Strecke $[G N]$ .

$[$ Ergebnisse: $\overline{FM}=1{,}04\;\text{cm};~\overline{GN}=0{,}58\;\text{cm}$ $]$

Lösung zu a

Berechne die Streckenlänge $\overline{FM}$

Verwende, dass das Dreieck BFM rechtwinklig ist.

Die Streckenlänge $\overline{BM}=4{,}5\; \mathrm{cm}$ im Dreieck ist gegeben.

Ebenso der Winkel $\sphericalangle BFM= 77°$ .

Verwende den Tangens im rechtwinkligen Dreieck, um die Seitenlänge $\overline{FM}$ zu berechnen.

Die Gegenkathete liegt dem Winkel gegenüber, die Ankathete direkt am Winkel.

Also ist $\overline{FM}$ die Ankathete und $\overline{BM}$ die Gegenkathete.

$\displaystyle tan(\sphericalangle BFM)$	$=$	$\displaystyle \frac{\overline{BM}}{\overline{FM}}$	$\displaystyle \cdot \overline{FM}$
$\displaystyle tan(\sphericalangle BFM)\cdot \overline{FM}$	$=$	$\displaystyle \overline{BM}$	$\displaystyle :tan(\sphericalangle BFM)$
$\displaystyle \overline{FM}$	$=$	$\displaystyle \frac{\overline{BM}}{tan(\sphericalangle BFM)}$
	↓	Setze die gegebenen Werte ein.
	$=$	$\displaystyle \frac{4{,}5}{\tan (77^{\circ })}$
	$=$	$\displaystyle 1{,}04\; \mathrm{cm}$

Berechne die Streckenlänge $\overline{GN}$

Verwende den Vierstreckensatz für die Strecken $\overline{FM}$ , $\overline{GN}$ , $\overline{BM}$ und $\overline{BN}$

Gegeben ist: $\overline{BM}= 4{,}5\;\mathrm{cm}$

Außerdem ist bekannt: $\overline{AN}=\overline{BN}$ wobei aufgrund der Achsensymmetrie des Axialschnitts gilt:

\displaystyle \overline{AN} =\overline{AC}:2 = 5\, \mathrm{cm}:2 = 2{,}5 \;\mathrm{cm}

Du hast gerade berechnet: $\overline{FM}= 1{,}04\;\mathrm{cm}$

Forme den Vierstreckensatz nach $\overline{GN}$ um:

$\displaystyle \frac{\overline{GN}}{\overline{FM}}$	$=$	$\displaystyle \frac{\overline{BN}}{\overline{BM}}$	$\displaystyle \cdot \overline{FM}$
$\displaystyle \overline{GN}$	$=$	$\displaystyle \frac{\overline{BN}}{\overline{BM}}\cdot \overline{FM}$
	↓	Setze die gegebenen Werte ein.
	$=$	$\displaystyle \frac{2{,}5\; }{4{,}5\;}\cdot 1{,}04$
	↓	Berechne.
	$=$	$\displaystyle 0{,}58\ \mathrm{cm}$

$\overline{GN} = 0{,}58 \ \mathrm{cm}$

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Berechnen Sie das Volumen $V$ eines solchen Spielzeugkreisels.

Lösung zu b

Das Volumen setzt sich zusammen aus:

einer halben Kugel
einem abgeschnittenen Kegel

Berechne das Volumen der Halbkugel

Wir benötigen die Hälfte des Kugelvolumens:

$\displaystyle V_{\text{Halbkugel}}$	$=$	$\displaystyle V_{\text{Kugel}}:2$
	↓	Setze die Formel für das Kugelvolumen ein.
	$=$	$\displaystyle \frac{4}{3}r^3\pi :2$
	↓	Fasse zusammen
	$=$	$\displaystyle \frac{2}{3}r^3\pi$
	↓	Der Radius r ist die Strecke $\overline{AN}= 2{,}5 \ \mathrm{cm}$
	$=$	$\displaystyle \frac{2}{3}\cdot (2{,}5\;\text{cm})^3\pi$
	↓	Berechne.
	$\approx ≈$	$\displaystyle 32{,}72\ \mathrm{cm}^3$

Berechne das Volumen des Kegelstumpfes

Das Volumen eines Kegelstumpfes erhält man, wenn man vom Volumen des großen Kegels das Volumen der abgeschnittenen Spitze, also das des kleinen Kegels abzieht.

Berechne zuerst das Volumen des großen Kegels:

Der Radius $r$ ist die Strecke $\overline{FM}= 1{,}04 \ \mathrm{cm}$ . Die Höhe $h$ ist die Strecke $\overline{BM}= 4{,}5\ \mathrm{cm}$ .

$\displaystyle V_{\text{Kegel1}}$	$=$	$\displaystyle \frac{1}{3}\ r^2\pi h$
	↓	Setze die Werte ein.
	$=$	$\displaystyle \frac{1}{3}\cdot (1{,}04\;\text{cm} )^2\cdot \pi \cdot 4{,}5\$
	↓	Berechne
	$\approx ≈$	$\displaystyle 5{,}10\ \mathrm{cm}^3$

Berechne anschließend das Volumen des kleinen Kegels, der in der Halbkugel steckt:

Der Radius $r$ ist die Strecke $\overline{GN}=0{,}58 \ \mathrm{cm}$ . Die Höhe $h$ ist die Strecke $\overline{BN}= \overline{AN}=2{,}5 \ \mathrm{cm}$ .

$\displaystyle V_{\text{Kegel2}}$	$=$	$\displaystyle \frac{1}{3}\ r^2\pi h$
	↓	Setze die Werte ein.
	$=$	$\displaystyle \frac{1}{3}\cdot (0{,}58\;\text{cm} )^2\cdot \pi \cdot 2{,}5$
	↓	Berechne
	$\approx ≈$	$\displaystyle 0{,}88\ \mathrm{cm}^3$

Ziehe das Volumen des kleinen Kegels vom großen Kegel ab:

$V_{Stumpf}=V_{Kegel1}-V_{Kegel2}= 5{,}10\ \mathrm{cm}^3 - 0{,}88 \ \mathrm{cm}^3= 4{,}22 \ \mathrm{cm}^3$

Setze die Volumina zusammen:

$V_{Kreisel} = V_{Halbkugel} + V_{Stumpf} = 32{,}72 \ \mathrm{cm}^3+4{,}22 \ \mathrm{cm}^3= 36{,}94 \ \mathrm{cm}^3$

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Teil A

Lösung zu a

Hast du eine Frage oder Feedback?

Lösung zu b

Hast du eine Frage oder Feedback?

Lösung zu c

Hast du eine Frage oder Feedback?

Lösung zu a

Hast du eine Frage oder Feedback?

Lösung zu b

Hast du eine Frage oder Feedback?

Lösung zu c

Hast du eine Frage oder Feedback?

Lösung zu d

Hast du eine Frage oder Feedback?

Lösung zu e

Hast du eine Frage oder Feedback?

Lösung zu a

Berechne die Streckenlänge FM‾\overline{FM}FM

Berechne die Streckenlänge GN‾\overline{GN}GN

Hast du eine Frage oder Feedback?

Lösung zu b

Berechne das Volumen der Halbkugel

Berechne das Volumen des Kegelstumpfes

Setze die Volumina zusammen:

Hast du eine Frage oder Feedback?

Berechne die Streckenlänge $\overline{FM}$

Berechne die Streckenlänge $\overline{GN}$