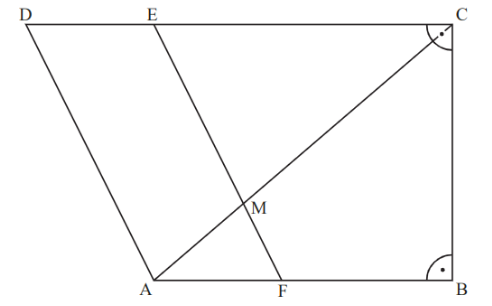
Die Zeichnung zeigt das Trapez . Der Punkt liegt auf der Strecke , der Punkt liegt auf der Strecke und die Diagonale schneidet die Strecke im Punkt .
Es gilt: ; ; ; ; =; .
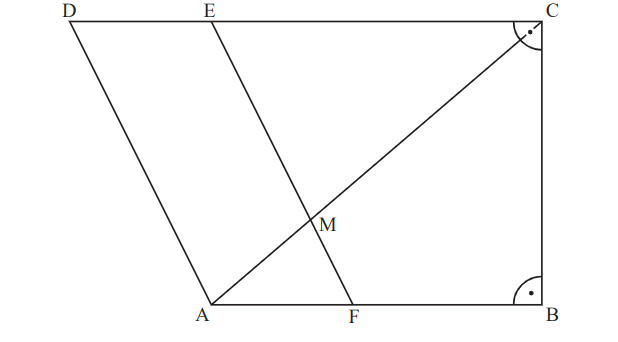
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
Berechnen Sie die Länge der Diagonalen sowie das Maß des Winkels .
Ergebnisse:
Zeigen Sie rechnerisch, dass für die Länge der Strecke gilt: .
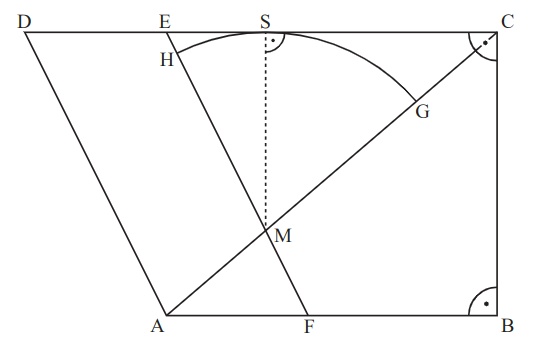
Ein Kreis um berührt die Strecke im Punkt und schneidet die Strecke im Punkt sowie die Strecke im Punkt .
Zeichnen Sie den Berührpunkt und den Kreisbogen in die Zeichnung zur Aufgabenstellung ein.
Berechnen Sie die Länge des Kreisbogens .
Teilergebnisse: