Nachtermin Teil A
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Die Aufgabenstellung findest Du hier als PDF.
- 1
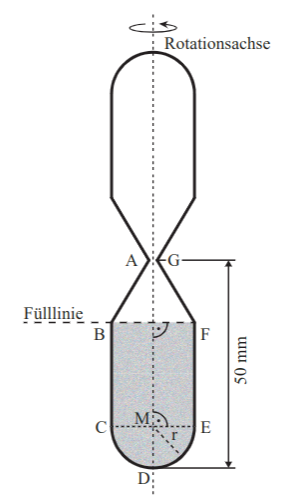
Nebenstehende Skizze zeigt den Axialschnitt eines Rotationskörpers, der das Glas einer Sanduhr darstellt.
Es gilt:
Die beiden Hälften des Glases sind jeweils hoch. Die untere Hälfte ist bis zur Fülllinie mit Sand gefüllt.
Wird die Sanduhr umgedreht, rieseln pro Sekunde durchschnittlich des Sandes von der oberen in die untere Hälfte des Glases. Berechnen Sie, nach welcher Zeit sich der Sand wieder vollständig in der unteren Hälfte des Glases befindet.
Runden Sie auf Ganze.
Teilergebnis:
- 2
In einem Wald leben derzeit Eichhörnchen. Man nimmt an, dass sich die Anzahl der Eichhörnchen nach Jahren näherungsweise durch die Funktion bestimmen lässt.
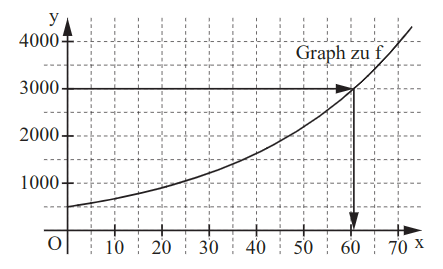
Ergänzen Sie die Wertetabelle auf Hunderter gerundet und zeichnen Sie sodann den Graphen der Funktion in das Koordinatensystem ein.
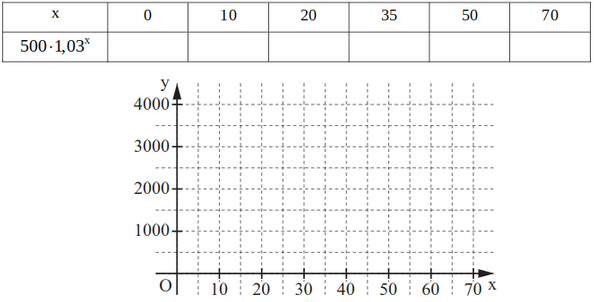
Bestimmen Sie mithilfe des Graphen der Funktion , nach wie vielen Jahren sich die ursprüngliche Anzahl der Eichhörnchen erstmals versechsfacht haben wird.
Ermitteln Sie rechnerisch, um wie viel Prozent die Anzahl der Eichhörnchen in einem Zeitraum von sieben Jahren zunehmen wird.
- 3
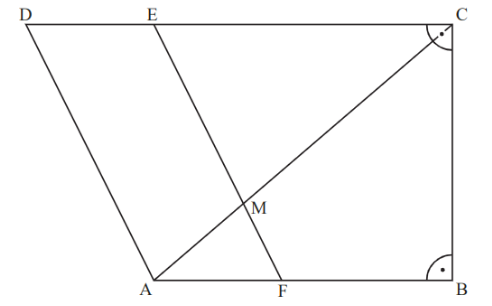
Die Zeichnung zeigt das Trapez . Der Punkt liegt auf der Strecke , der Punkt liegt auf der Strecke und die Diagonale schneidet die Strecke im Punkt .
Es gilt: ; ; ; ; =; .
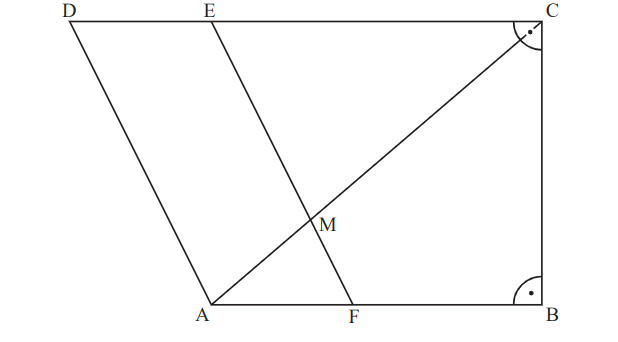
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
Berechnen Sie die Länge der Diagonalen sowie das Maß des Winkels .
Ergebnisse:
Zeigen Sie rechnerisch, dass für die Länge der Strecke gilt: .
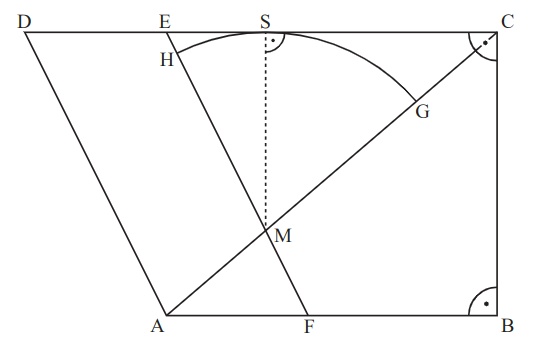
Ein Kreis um berührt die Strecke im Punkt und schneidet die Strecke im Punkt sowie die Strecke im Punkt .
Zeichnen Sie den Berührpunkt und den Kreisbogen in die Zeichnung zur Aufgabenstellung ein.
Berechnen Sie die Länge des Kreisbogens .
Teilergebnisse:
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?