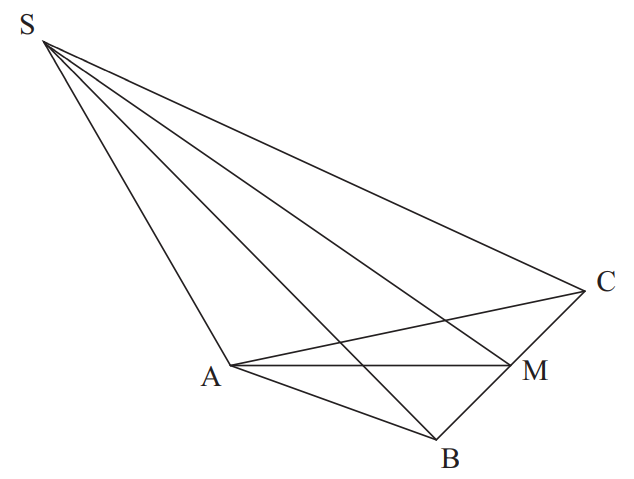
Zeichnen Sie ein Schrägbild der Pyramide ABCS, wobei $\left[AM\right]$ auf der Schrägbildachse und der Punkt A links vom Punkt M liegen soll.

Für die Zeichnung gilt: $q=\frac{1}{2}$; $\omega =45°$.

Zeichnen Sie die Höhe [SF] der Pyramide ABCS ein und berechnen Sie sodann deren Volumen.

Punkte $P_n$ auf [AS] bilden zusammen mit den Punkten B und C Dreiecke $P_{n}BC$. Die Winkel $P_{n}MA$ haben das Maß $\phi$ mit $\phi \in$ ]$0°;\mathrm{34,72}°$[ .

Zeichnen Sie das Dreieck $P_{1}BC$ für $\phi =20°$ in das Schrägbild zur Teilaufgabe (a) ein.

Zeigen Sie, dass für die Länge der Strecken $\left[M{P}_n\right]$ in Abhängigkeit von $\phi$ gilt:

$\overline{M{P}_n}\left(\phi \right)={\displaystyle \frac{\mathrm{5,20}}{\sin (120°+\phi )}}cm$ .

Unter den Dreiecken $P_{n}BC$ gibt es das gleichseitige Dreieck $P_{n}BC$ .

Bestimmen Sie rechnerisch das zugehörige Winkelmaß $\phi$.

Berechnen Sie das Volumen V der Pyramiden $ABC{P}_n$ mit der Grundfläche ABC und den Spitzen $P_n$ in Abhängigkeit von $\phi$ .

$[$Ergebnis : $V\left(\phi \right)={\displaystyle \frac{\mathrm{46,80}\cdot \sin \phi }{\sin (120°+\phi )}}c{m}^3$$]$

Die Pyramide $SBC{P}_3$ mit der Grundfläche SBC und der Spitze $P_3$ hat dasselbe Volumen wie die Pyramide $ABC{P}_3$ . Berechnen Sie das zugehörige Winkelmaß $\phi$.