🎓 Ui, fast schon Prüfungszeit? Hier geht's zur Mathe-Prüfungsvorbereitung.
Springe zum Inhalt oder Footer
SerloDie freie Lernplattform
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.

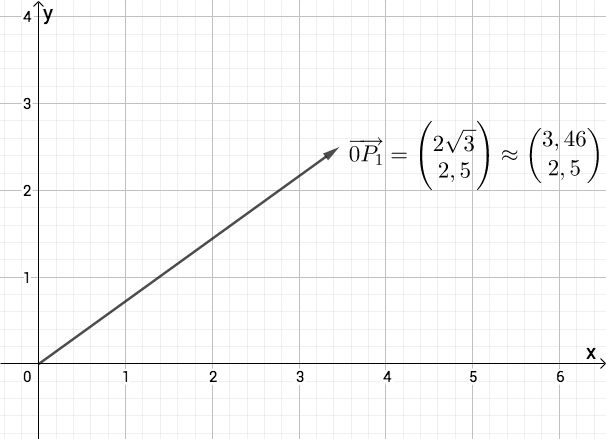
Gegeben sind der Punkt O(0∣0)O(0|0) und die Pfeile OP→n(φ)=(4⋅sin⁡(φ)5⋅cos⁡(φ))\overrightarrow{OP}_n(\varphi)=\begin{pmatrix}4\cdot\sin(\varphi)\\5\cdot\cos(\varphi)\end{pmatrix} mit φ∈[o∘;90∘[\varphi\in[o^\circ;90^\circ[.

  1. Zeichnen Sie den Pfeil OP1→\overrightarrow{OP_1} für φ=60∘\varphi=60^\circ in das Koordinatensystem ein.

    Bild

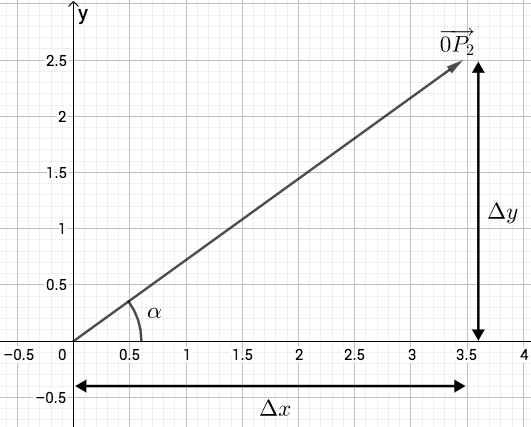
  2. Der Pfeil OP2→\overrightarrow{OP_2} schließt mit der positiven xx-Achse einen Winkel mit dem Maß α=20∘\alpha=20^\circ ein.

    Berechnen Sie die Koordinaten des Pfeils OP2→\overrightarrow{OP_2}.

  3. Der Pfeil OP3→\overrightarrow{OP_3} liegt auf der Winkelhalbierenden des 1. Quadraten.

    Berechnen Sie den zugehörigen Wert für φ\varphi und geben Sie die Koordinaten des Pfeils OP3→\overrightarrow{OP_3} auf zwei Stellen nach dem Komma an.