Nachtermin Teil A

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
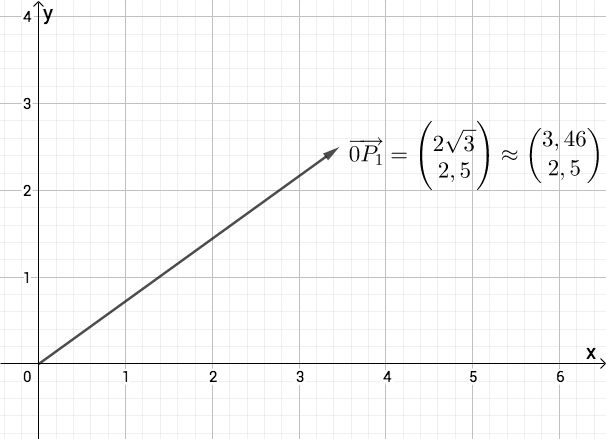
Gegeben sind der Punkt $O (0 | 0)$ und die Pfeile ${\vec{O P}}_{n} (φ) = (\begin{array}{c} 4 \cdot \sin (φ) \\ 5 \cdot \cos (φ) \end{array})$ mit $φ \in [o^{\circ}; 90^{\circ} [$ .
1. Zeichnen Sie den Pfeil $\vec{O P_{1}}$ für $φ = 60^{\circ}$ in das Koordinatensystem ein.
  
  Lösung zur Teilaufgabe a
  Für diese Aufgabe kannst du einen Blick auf die Sinus- und die Kosinusfunktion werfen.
  Mit deinem Taschenrechner berechnet du $\sin (60^{\circ}) = \frac{\sqrt{3}}{2}$ und $\cos (60^{\circ}) = 0,5$ .
  Du erhältst den Vektor:
  $\vec{0 P_{1}} = (\begin{array}{c} 4 \cdot \frac{\sqrt{3}}{2} \\ 5 \cdot 0,5 \end{array}) \approx (\begin{array}{c} 3,46 \\ 2,5 \end{array})$
  Diesen Vektor trägst du nun in ein Koordinatensystem ein und erhältst eine Zeichnung ähnlich zu der auf der linken Seite.
  Der Vektor eingetragen in ein Koordinatensystem
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
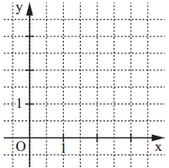
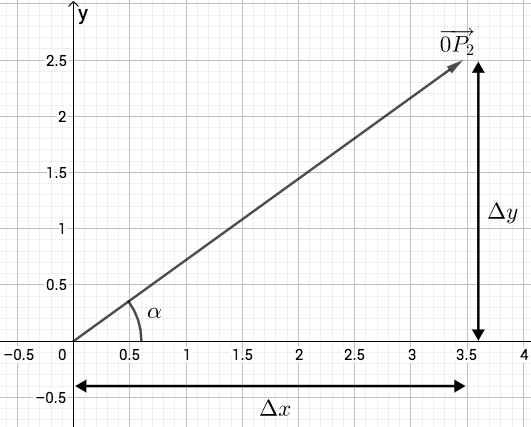
2. Der Pfeil $\vec{O P_{2}}$ schließt mit der positiven $x$ -Achse einen Winkel mit dem Maß $α = 20^{\circ}$ ein.
  Berechnen Sie die Koordinaten des Pfeils $\vec{O P_{2}}$ .
  
  Lösung zur Teilaufgabe b
  Du bestimmst den Steigungswinkel $α$ gemäß
  $\tan (α) = \frac{Δ y}{Δ x} .$
  Hier ist $Δ x = 4 \cdot \sin (φ) - 0$ und
  $Δ y = 5 \cdot \cos (φ) - 0$ . Damit erhältst du
  $\tan (α) = \frac{5}{4 \cdot \tan (φ)}$ , sodass
  $φ = \arctan (\frac{5}{4 \cdot \tan (20^{\circ})}) \approx {73,77}^{\circ} .$
  Steigungswinkel eines Vektors
  Du hast also insgesamt den Vektor
  $\vec{0 P_{2}} = (\begin{array}{c} 4 \cdot \sin ({73,77}^{\circ}) \\ 5 \cdot \cos ({73,77}^{\circ}) \end{array}) \approx (\begin{array}{c} 3,84 \\ 1,39 \end{array})$
  berechnet.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Der Pfeil $\vec{O P_{3}}$ liegt auf der Winkelhalbierenden des 1. Quadraten.
  Berechnen Sie den zugehörigen Wert für $φ$ und geben Sie die Koordinaten des Pfeils $\vec{O P_{3}}$ auf zwei Stellen nach dem Komma an.
  
  Lösung zur Teilaufgabe c
  Auch hier benötigst du lediglich Wissen zu der Sinus- und der Kosinusfunktion.
  Für die Winkelhalbierende des ersten Quadranten gilt definitionsgemäß $α = 45^{\circ}$ . Erinnere dich an die Beziehung
  $φ = \arctan (\frac{5}{4 \cdot \tan (α)})$
  aus Teilaufgabe (b). Setzt du nun $α = 45^{\circ}$ ein und verwendest deinen Taschenrechner, so erhältst du $φ \approx {51,34}^{\circ}$ .
  Insgesamt hast du also den Vektor
  $\vec{0 P_{3}} = (\begin{array}{c} 4 \cdot \sin ({51,34}^{\circ}) \\ 5 \cdot \cos ({51,34}^{\circ}) \end{array}) \approx (\begin{array}{c} 3,12 \\ 3,12 \end{array})$
  berechnet.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Gegeben sind die Funktionen $f_{1}$ mit der Gleichung $y = 2 \cdot (x + 2,5)^{\frac{1}{2}} - 4$ und $f_{2}$ mit der Gleichung $y = - 1,5 \cdot (x + 2,5)^{\frac{1}{2}} + 3 (𝔾 = ℝ \times ℝ)$ .
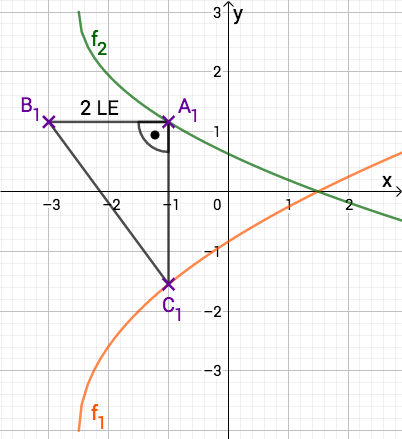
Im Koordinatensystem ist der Graph zu $f_{1}$ eingezeichnet.
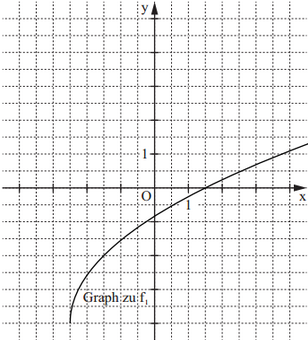
Darstellung des Graphen von $f_{1}$
1. Der Graph zu $f_{1}$ kann durch orthogonale Affinität mit der x-Achse als Affinitätsachse und $k$ als Affinitätsmaßstab ( $k \in ℝ ∖ {0}$ ) auf den Graphen zu $f_{2}$ abgebildet werden.
  Bestimmen Sie den Affinitätsmaßstab $k$ und geben Sie die Definitions- und Wertemenge der Funktion $f_{2}$ an.
  Zeichnen Sie sodann den Graphen zu $f_{2}$ in das Koordinatensystem zur Aufgabenstellung ein.
  
  Lösung zur Teilaufgabe a
  Für diese Aufgabe benötigst du ein grundlegendes Wissen über Definitions- und Wertebereich einer Funktion.
  Gesucht ist ein Faktor $k \in ℝ ∖ {0}$ , sodass $f_{2} = k \cdot f_{1}$ . Durch Vergleich der Vorfaktoren des Terms $(x + 2,5)^{\frac{1}{2}}$ erkennst du, dass
  $k = - \frac{1,5}{2} = - \frac{3}{4} = - 0,75.$
  Du kannst dir das Ganze auch nochmal in dem Applet unten anschauen:
  Die Funktion $f_{2}$ kann nur dort definiert sein, wo das Argument der Quadratwurzel nicht negativ ist. Das ist genau dann der Fall, wenn
  $x + 2,5$ $\geq$ $0$ $- 2,5$
  $x$ $\geq$ $- 2,5$
  Also ist der Definitionsbereich der Funktion $f_{2}$ gegeben durch $D_{f_{2}} = [- 2,5, \infty [$ .
  Für den Wertebereich der Funktion $f_{2}$ liest du aus dem Funktionsgraphen ab:
  $W_{f_{2}} =] - \infty, 3]$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Punkte $A_{n} (x | - 1,5 \cdot (x + 2,5)^{\frac{1}{2}} + 3)$ auf dem Graph zu $f_{2}$ und Punkte $C_{n} (x | 2 \cdot (x + 2,5)^{\frac{1}{2}} - 4)$ auf dem Graphen $f_{1}$ haben dieselbe Abszisse $x$ und sind für $x < 1,5$ zusammen mit Punkten $B_{n}$ die Eckpunkte von rechtwinkligen Dreiecken $A_{n} B_{n} C_{n}$ mit den Hypotenusen $[B_{n} C_{n}]$ .
  Es gilt: $A_{n} B_{n} = 2 LE$ .
  Zeichnen Sie das Dreieck $A_{1} B_{1} C_{1}$ für $x = - 1$ in das Koordinatensystem zur Aufgabenstellung ein.
  
  Lösung zur Teilaufgabe b
  Du startest mit den Punkten $A_{1}$ und $C_{1}$ . Beide Punkte liegen auf der Geraden $x = - 1$ und die $y$ -Koordinaten sind durch $f_{2} (- 1) \approx 1,16$ für $A_{1}$ sowie durch $f_{1} (- 1) \approx - 1,55$ für $C_{1}$ gegeben. Ferner weißt du, dass $[B_{1} C_{1}]$ die Hypotenuse des Dreiecks werden wird. Daher ist der Winkel $∢ B_{1} A_{1} C_{1}$ rechtwinklig. Da die Eckpunkte von Dreiecken stets gegen den Uhrzeigersinn bezeichnet werden, muss $B_{1}$ links von $A_{1}$ liegen. Du zeichnest also die Normale zur Strecke $[A_{1} C_{1}]$ durch den Punkt $A_{1}$ ein und trägst die gegebenen $A_{1} B_{1} = 2 LE$ nach links ab. Dort liegt $B_{1}$ .
  Dreieck in das Koordinatensystem eingezeichnet
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Zeigen Sie durch Rechnung, dass für die Längen der Strecken $[A_{n} C_{n}]$ in Abhängigkeit von der Abszisse $x$ der Punkte $A_{n}$ gilt:
  $A_{n} C_{n} (x) = [- 3,5 \cdot (x + 2,5)^{\frac{1}{2}} + 7] LE$
  
  Lösung zur Teilaufgabe c
  Da die Punkte $A_{n}$ und $C_{n}$ stets die gleiche $x$ -Koordinate besitzen, ist die Länge der Strecke $[A_{n} C_{n}]$ durch die Differenz der $y$ -Koordinaten gegeben. Du berechnest:
  $A_{n} C_{n} (x)$ $=$ $(- 1,5 \cdot (x + 2,5)^{\frac{1}{2}} + 3) - (2 \cdot (x + 2,5)^{\frac{1}{2}} - 4)$
  $=$ $- 3,5 \cdot (x + 2,5)^{\frac{1}{2}} + 7 (LE)$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
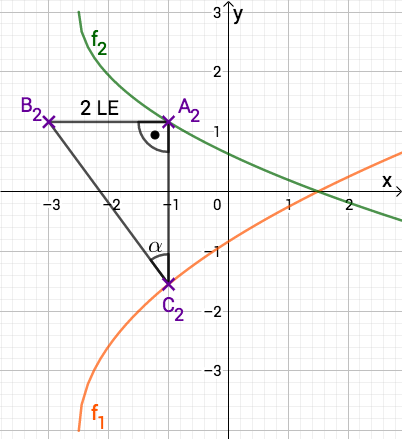
4. Im Dreieck $A_{2} B_{2} C_{2}$ gilt: $∢ A_{2} C_{2} B_{2} = 40^{\circ}$ .
  Berechnen Sie den zugehörigen Wert für $x$ auf zwei Stellen nach dem Komma gerundet.
  
  Lösung zur Teilaufgabe d
  Für diese Aufgabe lohnt sich ein Blick in den Artikel über trigonometrische Beziehungen.
  Der Winkel $∢ A_{1} C_{1} B_{1}$ wird im Folgenden mit $α$ bezeichnet. Schau dir dazu auch die nicht maßstabsgetreue Skizze auf der rechten Seite an. Wir benutzen die Tangensformel
  $\tan (α) = \frac{Gegenkathete}{Ankathete}$
  im rechtwinkligen Dreieck $A_{2} B_{2} C_{2}$ . Hier ist $[A_{2} B_{2}]$ die Gegenkathete und $[A_{2} C_{2}]$ die Ankathete. Wir lösen diese Beziehung nach der Ankathete auf und erhalten
  Skizze des Dreiecks mit dem zu bestimmenden Winkel
  $A_{2} C_{2}$ $=$ $\frac{A_{2} B_{2}}{\tan α}$
  $=$ $\frac{2}{\tan (40 °)}$
  $\approx$ $2,38 (LE)$
  Nun löst du die in Teilaufgabe (c) bestimmte Gleichung nach $x$ auf:
  $A_{2} C_{2}$ $=$ $- 3,5 \cdot (x + 2,5)^{\frac{1}{2}} + 7$ $- 7$
  $A_{2} C_{2} - 7$ $=$ $- 3,5 \cdot (x + 2,5)^{\frac{1}{2}}$ $: (- 3,5)$
  $- \frac{A_{2} C_{2} - 7}{3,5}$ $=$ $(x + 2,5)^{\frac{1}{2}}$ $()^{2}$
  ${(- \frac{A_{2} C_{2} - 7}{3,5})}^{2}$ $=$ $x + 2,5$ $- 2,5 und Seiten vertauschen$
  $x$ $=$ ${(\frac{A_{2} C_{2} - 7}{3,5})}^{2} - 2,5$
  Abschließend setzt du $A_{2} C_{2} \approx 2,38$ ein und erhältst $x \approx - 0,76$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
5. Begründen Sie, dass für den Flächeninhalt $A$ der Dreiecke $A_{n} B_{n} C_{n}$ gilt: $A \leq 7 FE$ .
  
  Lösung zur Teilaufgabe e
  Hier benutzt du Resultate über den Flächeninhalt von Dreiecken.
  Da das Dreieck $A_{n} B_{n} C_{n}$ rechtwinklig ist, kannst du dessen Flächeninhalt gemäß
  $A (x) = \frac{1}{2} \cdot A_{n} B_{n} \cdot A_{n} C_{n} (x)$
  berechnen (siehe hierzu den "Sonderfall rechtwinkliges Dreieck" im Artikel über den Flächeninhalt). Du setzt $A_{n} B_{n} = 2 LE$ und das Resultat für $A_{n} C_{n} (x)$ aus Teilaufgabe (c) ein und erhältst:
  $A (x) = \frac{1}{2} \cdot 2 \cdot (- 3,5 \cdot (x + 2,5)^{\frac{1}{2}} + 7) = (\underset{\leq 0}{\underset{⏟}{- 3,5 \cdot \underset{\geq 0}{\underset{⏟}{(x + 2,5)^{\frac{1}{2}}}}}} + 7) (F E) \leq 7 (F E)$
  Hier hast du benutzt, dass die Quadratwurzel (falls definiert) stets nicht-negativ, d.h. $\geq 0$ , ist.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
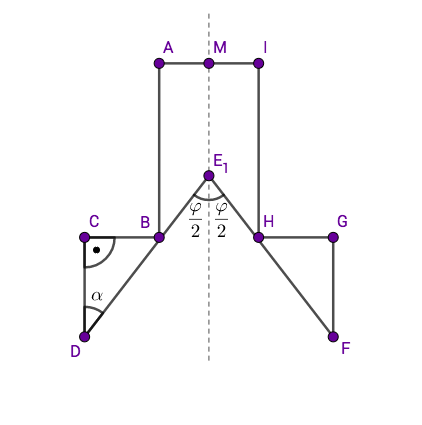
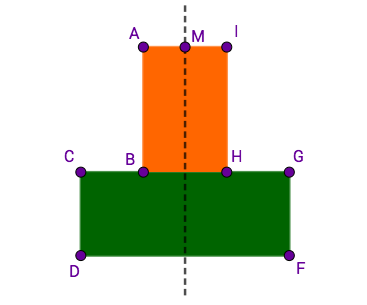
Die Axialschnitte von Rotationskörpern sind symmetrische Neunecke $A B C D E_{n} F G H I$ mit der Symmetrieachse $M P$ .
Punkte $E_{n}$ au der Symmetrieachse $M P$ legen zusammen mit den Punkten $D$ und $F$ Winkel $D E_{n} F$ fest. Die Winkel $D E_{n} F$ haben das Maß $φ \in] {55,02}^{\circ}; 180^{\circ} [$ .
Es gilt:
$\begin{array}{l} A B = 6 cm; B C = 2,5 cm, C D = 4,8 cm; A I = 4 cm \\ ∢ D C B = 90^{\circ}; ∢ A B C = 90^{\circ}, ∢ B A I = 90^{\circ} \end{array}$
Die Skizze zeigt das maßstabsgetreue Neuneck $A B C D E_{1} F G H I$ für $φ = 75^{\circ}$ .
1. Begründen Sie durch Rechnung das Maß der unteren Intervallgrenze für $φ$ .
  
  Lösung zur Teilaufgabe a
  Hier benutzt du Kenntnisse über Wechselwinkel und trigonometrische Beziehungen.
  Der kleinste mögliche Winkel $φ$ wird dann erreicht, wenn $E_{1}$ so gewählt wird, dass die Strecke $[D E_{1}]$ den Punkt $B$ berührt. In diesem Fall berührt die Strecke $[E_{1} F]$ auch den Punkt $H$ aus Symmetriegründen. Diese Situation ist in der linken Zeichnung zu sehen. Erinnere dich, dass die Winkel $α$ und $φ : 2$ als Wechselwinkel in Beziehung stehen. Daher reicht es, den Winkel $α$ im rechtwinkligen Dreieck $C D B$ zu bestimmen. Aus der Formelsammlung nimmst du die Beziehung:
  $\tan (α) = \frac{Gegenkathete}{Ankathete} .$
  In diesem Problem ist die Gegenkathete die Strecke $[B C]$ und die Ankathete die Strecke $[C D]$ . Damit berechnest du
  $\tan (α) = \frac{B C}{C D} = \frac{2,5 cm}{4,8 cm} .$
  Wende nun die Umkehrfunktion des Tangens an und du erhältst $α = {27,51}^{\circ}$ .
  Damit hast du den kleinstmöglichen Winkel $φ = 2 \cdot α = 2 \cdot {27,51}^{\circ} = {55,02}^{\circ}$ bestimmt.
  Skizze der Figur
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Zeigen Sie durch Rechnung, dass für das Volumen $V$ der Rotationskörper in Abhängigkeit von $φ$ gilt: $V (φ) = π \cdot (121,2 - \frac{30,375}{\tan \frac{φ}{2}}) {cm}^{3}$
  
  Lösung zur Teilaufgabe b
  In dieser Aufgabe verwendest du Inhalte aus den Artikeln Rotationskörper und trigonometrische Beziehungen.
  Du berechnest zunächst das größere Volumen des Rotationskörpers erzeugt von der linksstehenden Abbildung und ziehst danach die Aussparung ab. Dazu gehst du in zwei Schritten vor. Du startest mit dem Rotationskörper, erzeugt von dem orangen Rechteck. Dies ist ein Zylinder mit Höhe $A B$ und Radius $I M = A I : 2$ . Analog verfährst du mit dem grünen Rechteck. Dort ist die Höhe $C D$ und der Radius $D F : 2 = A I : 2 + B C$ .
  Skizze des gesamten Körpers
  Du wendest nun die Zylinderformel an und erhältst
  $V_{orange} = π \cdot r^{2} \cdot h = π \cdot {(\frac{A I}{2})}^{2} \cdot A B = π \cdot {(\frac{4}{2})}^{2} \cdot 6 = 24 \cdot π {cm}^{3}$
  sowie
  $V_{grün} = π \cdot r^{2} \cdot h = π \cdot {(\frac{A I}{2} + B C)}^{2} \cdot C D = π \cdot {(\frac{4}{2} + 2,5)}^{2} \cdot 4,8 = 97,2 \cdot π {cm}^{3} .$
  Nun musst du abschließend noch berechnen, wie viel Volumen der Rotationskörper, erzeugt durch das Dreieck $D E_{1} F$ , beiträgt. Das rotierende Dreieck ergibt einen Kegel mit Spitze $E_{1}$ . Der Radius der Grundfläche des Kegels ist wie zuvor $D F : 2$ . Für die Höhe betrachtest du das Dreieck $D P E_{1}$ (siehe Skizze der Aufgabenstellung) und verwendest wie in Teilaufgabe A3.1 die Tangensbeziehung:
  $\tan (\frac{φ}{2}) = \frac{Gegenkathete}{Ankathete}$
  Hier ist nun die Gegenkathete durch $[D P]$ und die Ankathete durch $[E_{1} P]$ gegeben. Letztere Strecke ist gleichzeitig die Höhe des Kegels, für dessen Volumen du dich interessierst. Du löst also nach dieser auf und erhältst
  $h = E_{1} P = \frac{D P}{\tan (\frac{φ}{2})} = \frac{r}{\tan (\frac{φ}{2})} .$
  Das setzt du jetzt in die Kegelformel ein und erhältst
  $V_{Kegel} = \frac{π}{3} \cdot r^{2} \cdot h = \frac{π}{3} \cdot \frac{r^{3}}{\tan (\frac{φ}{2})} = \frac{π}{3} \frac{{(D F : 2)}^{3}}{\tan (\frac{φ}{2})} = \frac{π}{3} \frac{{4,5}^{3}}{\tan (\frac{φ}{2})} = \frac{30,375 \cdot π}{\tan (\frac{φ}{2})} {cm}^{3}$
  Nun kannst du das Volumen $V$ des Rotationskörpers bestimmen:
  $V (φ)$ $=$ $V_{orange} + V_{grün} - V_{Zylinder}$
  $=$ $24 \cdot π {cm}^{3} + 97,2 \cdot π {cm}^{3} - \frac{30,375 \cdot π}{\tan (\frac{φ}{2})}$
  $=$ $π \cdot (24 + 97,2 - \frac{30,375}{\tan (\frac{φ}{2})})$
  $=$ $π \cdot (121,2 - \frac{30,375}{\tan (\frac{φ}{2})})$
  Das ist genau die Formel, welche die Angabe als Vergleichsergebnis nennt.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Berechnen Sie das Volumen des Rotationskörpers für $φ = 70^{\circ}$ auf zwei Stellen nach dem Komma genau.
  
  Lösung zur Teilaufgabe c
  Du setzt $70^{\circ}$ in die hergeleitete Volumenformel aus Teilaufgabe (b) ein und erhältst unter Verwendung deines Taschenrechners
  $V (70^{\circ}) \approx 244,48 {cm}^{3} .$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$A_{n} C_{n} (x)$	$=$	$(- 1,5 \cdot (x + 2,5)^{\frac{1}{2}} + 3) - (2 \cdot (x + 2,5)^{\frac{1}{2}} - 4)$
	$=$	$- 3,5 \cdot (x + 2,5)^{\frac{1}{2}} + 7 (LE)$

$A_{2} C_{2}$	$=$	$\frac{A_{2} B_{2}}{\tan α}$
	$=$	$\frac{2}{\tan (40 °)}$
	$\approx$	$2,38 (LE)$

$A_{2} C_{2}$	$=$	$- 3,5 \cdot (x + 2,5)^{\frac{1}{2}} + 7$	$- 7$
$A_{2} C_{2} - 7$	$=$	$- 3,5 \cdot (x + 2,5)^{\frac{1}{2}}$	$: (- 3,5)$
$- \frac{A_{2} C_{2} - 7}{3,5}$	$=$	$(x + 2,5)^{\frac{1}{2}}$	$()^{2}$
${(- \frac{A_{2} C_{2} - 7}{3,5})}^{2}$	$=$	$x + 2,5$	$- 2,5 und Seiten vertauschen$
$x$	$=$	${(\frac{A_{2} C_{2} - 7}{3,5})}^{2} - 2,5$

$V (φ)$	$=$	$V_{orange} + V_{grün} - V_{Zylinder}$
	$=$	$24 \cdot π {cm}^{3} + 97,2 \cdot π {cm}^{3} - \frac{30,375 \cdot π}{\tan (\frac{φ}{2})}$
	$=$	$π \cdot (24 + 97,2 - \frac{30,375}{\tan (\frac{φ}{2})})$
	$=$	$π \cdot (121,2 - \frac{30,375}{\tan (\frac{φ}{2})})$

Nachtermin Teil A

Lösung zur Teilaufgabe a

Hast du eine Frage oder Feedback?

Lösung zur Teilaufgabe b

Hast du eine Frage oder Feedback?

Lösung zur Teilaufgabe c

Hast du eine Frage oder Feedback?

Lösung zur Teilaufgabe a

Hast du eine Frage oder Feedback?

Lösung zur Teilaufgabe b

Hast du eine Frage oder Feedback?

Lösung zur Teilaufgabe c

Hast du eine Frage oder Feedback?

Lösung zur Teilaufgabe d

Hast du eine Frage oder Feedback?

Lösung zur Teilaufgabe e

Hast du eine Frage oder Feedback?

Lösung zur Teilaufgabe a

Hast du eine Frage oder Feedback?

Lösung zur Teilaufgabe b

Hast du eine Frage oder Feedback?

Lösung zur Teilaufgabe c

Hast du eine Frage oder Feedback?