Nachtermin Teil A - lernen mit Serlo!

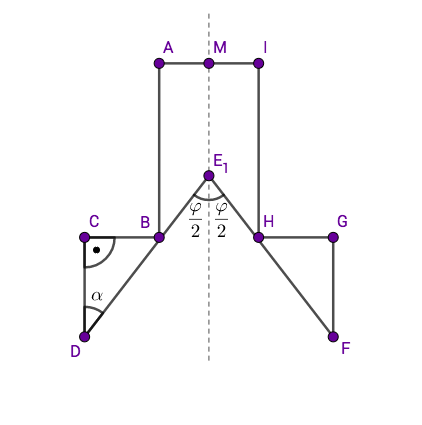
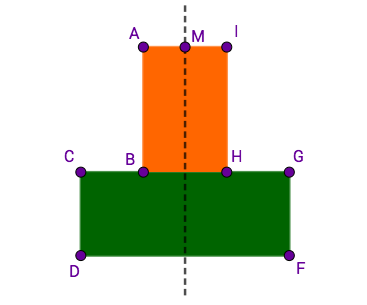
Die Axialschnitte von Rotationskörpern sind symmetrische Neunecke $ABCDE_nFGHI$ mit der Symmetrieachse $MP$ .

Punkte $E_n$ au der Symmetrieachse $MP$ legen zusammen mit den Punkten $D$ und $F$ Winkel $DE_nF$ fest. Die Winkel $DE_nF$ haben das Maß $\varphi\in]55{,}02^\circ;180^\circ[$ .

Es gilt:

$\overline{AB}=6~\text{cm};~\overline{BC}=2{,}5~\text{cm},~\overline{CD}=4{,}8~\text{cm};~\overline{AI}=4~\text{cm}\\\sphericalangle DCB=90^\circ;~\sphericalangle ABC=90^\circ,~\sphericalangle BAI=90^\circ$

Die Skizze zeigt das maßstabsgetreue Neuneck $ABCDE_1FGHI$ für $\varphi=75^\circ$ .

Begründen Sie durch Rechnung das Maß der unteren Intervallgrenze für $\varphi$ .

Lösung zur Teilaufgabe a
Hier benutzt du Kenntnisse über Wechselwinkel und trigonometrische Beziehungen.
Der kleinste mögliche Winkel $\varphi$ wird dann erreicht, wenn $E_1$ so gewählt wird, dass die Strecke $[DE_1]$ den Punkt $B$ berührt. In diesem Fall berührt die Strecke $[E_1F]$ auch den Punkt $H$ aus Symmetriegründen. Diese Situation ist in der linken Zeichnung zu sehen. Erinnere dich, dass die Winkel $\alpha$ und $\varphi:2$ als Wechselwinkel in Beziehung stehen. Daher reicht es, den Winkel $\alpha$ im rechtwinkligen Dreieck $CDB$ zu bestimmen. Aus der Formelsammlung nimmst du die Beziehung:
$\displaystyle\tan(\alpha)=\frac{\text{Gegenkathete}}{\text{Ankathete}}.$
In diesem Problem ist die Gegenkathete die Strecke $[BC]$ und die Ankathete die Strecke $[CD]$ . Damit berechnest du
Wende nun die Umkehrfunktion des Tangens an und du erhältst $\alpha=27{,}51^\circ$ .
Damit hast du den kleinstmöglichen Winkel $\varphi=2\cdot\alpha=2\cdot27{,}51^\circ=55{,}02^\circ$ bestimmt.
Skizze der Figur
Hast du eine Frage oder Feedback?
Kommentiere hier 👇

Zeigen Sie durch Rechnung, dass für das Volumen $V$ der Rotationskörper in Abhängigkeit von $\varphi$ gilt: $V(\varphi)=\pi\cdot\left(121{,}2-\dfrac{30{,}375}{\tan\frac{\varphi}{2}}\right)~\text{cm}^3$

Berechnen Sie das Volumen des Rotationskörpers für $\varphi=70^\circ$ auf zwei Stellen nach dem Komma genau.

Lösung zur Teilaufgabe c
Du setzt $70^\circ$ in die hergeleitete Volumenformel aus Teilaufgabe (b) ein und erhältst unter Verwendung deines Taschenrechners
Hast du eine Frage oder Feedback?
Kommentiere hier 👇

$\displaystyle V(\varphi )$	$=$	$\displaystyle V_{\text{orange}}+V_{\text{grün}}-V_{\text{Zylinder}}$
	$=$	$\displaystyle 24\cdot\pi\,\mathrm{cm}^3+97{,}2\cdot\pi\,\mathrm{cm}^3-\frac{30{,}375\cdot\pi}{\tan\left(\frac{\varphi}{2}\right)}$
	$=$	$\displaystyle \pi \cdot \left(24+97{,}2-\frac{30{,}375}{\tan \left(\frac{\varphi }{2}\right)}\right)$
	$=$	$\displaystyle \pi \cdot \left(121{,}2-\frac{30{,}375}{\tan \left(\frac{\varphi }{2}\right)}\right)$

Lösung zur Teilaufgabe a

Hast du eine Frage oder Feedback?

Lösung zur Teilaufgabe b

Hast du eine Frage oder Feedback?

Lösung zur Teilaufgabe c

Hast du eine Frage oder Feedback?