Trigonometrische Umkehrfunktionen

Die Funktionen Arkussinus, Arkuskosinus und Arkustangens (gebräuchlich sind die Bezeichnungen $\arcsin,\sin^{-1},\mathrm{asin}$ ) sind die Umkehrfunktionen der trigonometrischen Funktionen Sinus, Kosinus und Tangens, das heißt, sie ordnen einem Verhältnis einen Winkel zu.

Ist beispielsweise $\cos\left(\alpha\right)=x$ , so folgt $\arccos(x)=\alpha$ durch Anwendung des Arkuskosinus.

Definitions- und Wertemengen

Funktion	Definitionsmenge	Wertemenge
$\arcsin(x)$	$D = [-1;1]$	$W = \left[-\frac{\pi}{2}; \frac{\pi}{2}\right]$
$\arccos(x)$	$D = [-1;1]$	$W = [0; \pi]$
$\arctan(x)$	$D = \mathbb{R}$	$W = \left]-\frac{\pi}{2};\frac{\pi}{2} \right[$

Graphen

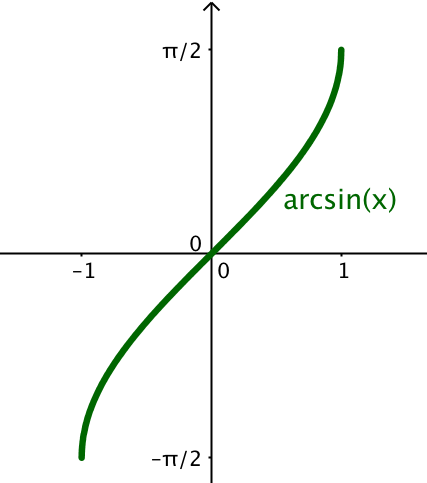
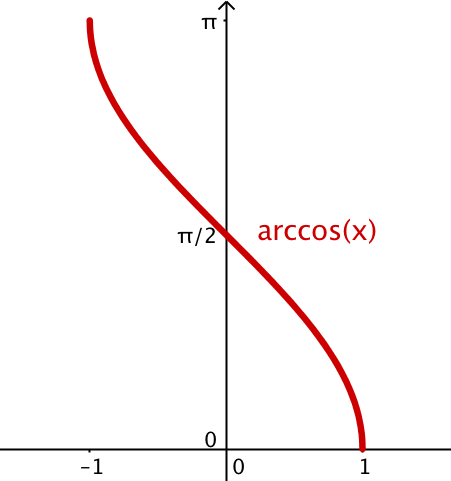
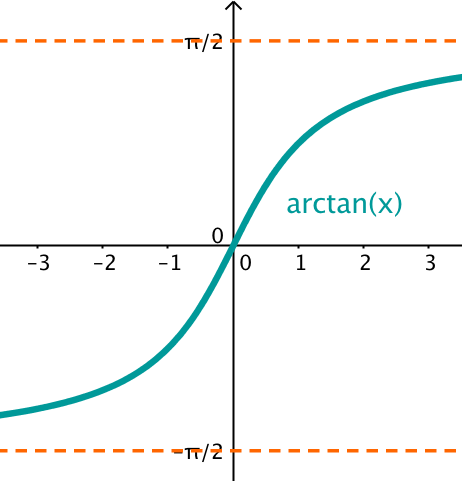
Beispiel

$\displaystyle \sin(x+\pi)$	$=$	$\displaystyle 1$
	↓	Wende auf beiden Seiten die Umkehrfunktion $\arcsin$ an.
$\displaystyle x+\pi$	$=$	$\displaystyle \arcsin(1)$
	↓	Löse nach $x$ auf.
$\displaystyle x$	$=$	$\displaystyle \arcsin(1)-\pi$
	↓	Verwende, dass $\arcsin(1)=\frac{\pi}{2}.$ Betrachte hierzu den obigen Graphen von Arkussinus.
$\displaystyle x$	$=$	$\displaystyle -\frac{\pi}{2}$

Ableitungen

Die Ableitungen der trigonometrischen Umkehrfunktionen lassen sich mithilfe der Regel für die Ableitung einer Umkehrfunktion ermiteln:

Funktion	Ableitung
$\arcsin(x)$	$\arcsin'(x) = \frac1{\sqrt{1-x^2}}$
$\arccos(x)$	$\arccos'(x) = -\frac1{\sqrt{1-x^2}}$
$\arctan(x)$	$\arctan'(x) = \frac1{1+x^2}$

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?