Tangensfunktion

Die Tangensfunktion ist definiert als:

\tan (x) = \frac{\sin (x)}{\cos (x)}

Eigenschaften der Tangensfunktion

Der Tangens hat folgende Eigenschaften:

Die Nullstellen sind die gleichen wie beim Sinus, da dieser im Zähler des Bruches steht: $\dots, - 3 π, - 2 π, - π, 0, π, 2 π, 3 π, \dots$ .
Der Definitionsbereich des Tangens sind die gesamten reellen Zahlen $(ℝ)$ bis auf die Definitionslücken: $\dots, - \frac{3 π}{2}, - \frac{π}{2}, \frac{π}{2}, \frac{3 π}{2}, \dots$ . Diese Definitionslücken des Tangens sind genau die Nullstellen des Kosinus, da man sonst durch $0$ teilen müsste. Bei den Definitionslücken befinden sich die Asymptoten der Tangensfunktion.
Der Wertebereich der Tangensfunktion geht von $- \infty$ bis $+ \infty$ . Das entspricht den gesamten reellen Zahlen $(ℝ)$ .
Der Tangens hat keine Extrema.

Beispiel zum Rechnen mit der Tangensfunktion

Zeichne die Funktion $f (x) = \tan (x) \cos (x)$ im offenen Intervall $] - \frac{π}{2}, \frac{π}{2} [$ in ein Koordinatensystem.

Verwende die Definition der Tangensfunktion, das heißt $\tan (x) = \frac{\sin (x)}{\cos (x)}$

f (x) = \frac{\sin (x)}{\cos (x)} \cdot \cos (x)

Kürze die Kosinusfunktion, da sie sowohl im Zähler, als auch im Nenner steht.

$f (x) = \sin (x)$

Bemerkung: Wie im obigen Artikel beschrieben, hat die Tangensfunktion Definitionlücken an den ungeradzahligen Vielfachen von $\frac{π}{2}$ . Bei der Funktion $f (x) = \tan (x) \cos (x)$ lassen sich diese Lücken beheben. Zur Erinnerung: Hebbare Definitionslücken

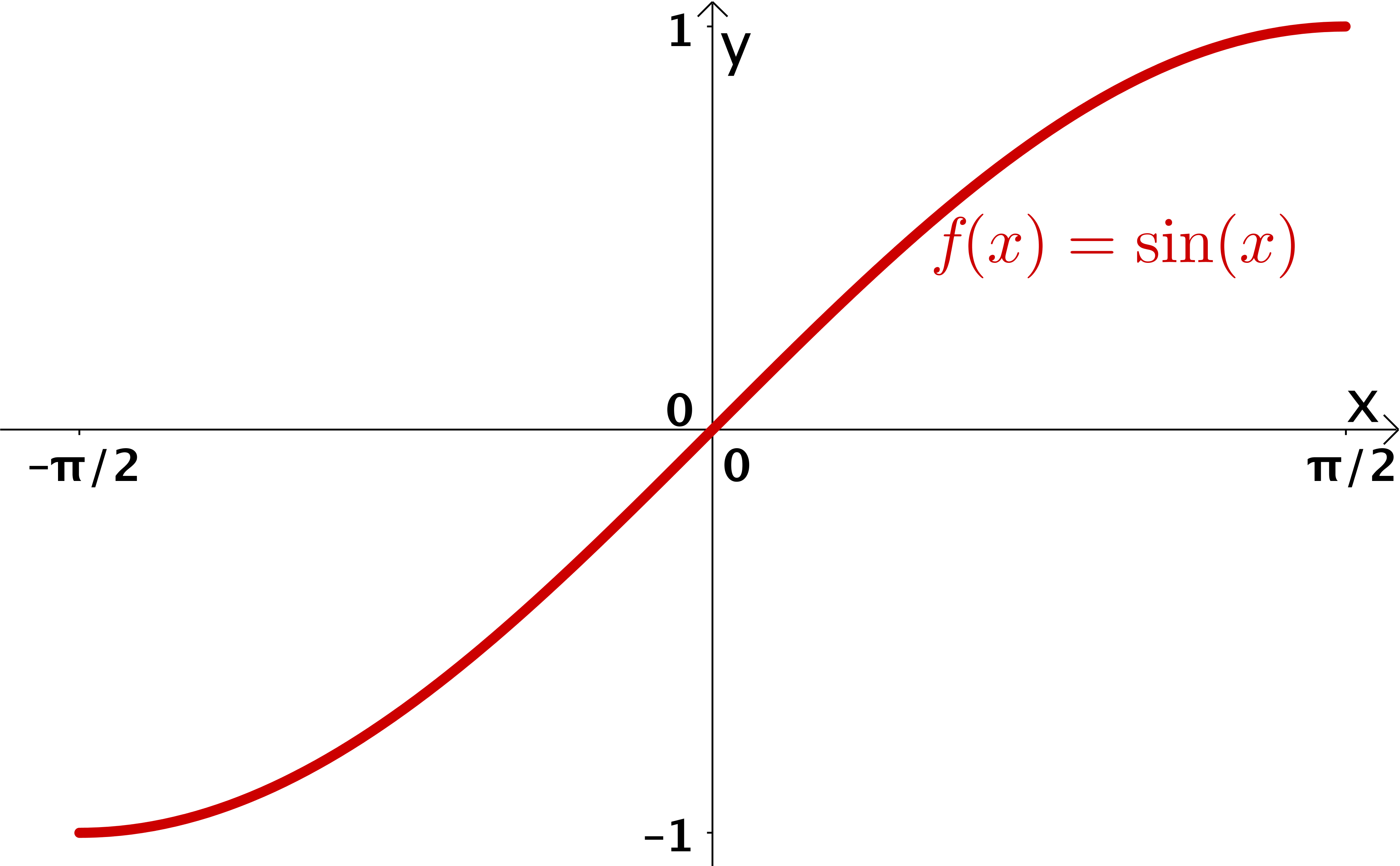
Video zu Sinus, Kosinus und Tangensfunktion

Laden

Übungsaufgaben

Laden

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?