Umkehrfunktion

Die Umkehrfunktion einer Funktion $f$ ist die Funktion $f^{-1}$ , die jedem Funktionswert sein Argument zuordnet:

$f^{-1}\left(f(x)\right)=x$ und $f\left(f^{-1}(x)\right)=x$

Achtung: Die Schreibweise $f^{-1}$ hat nichts mit dem Kehrwert zu tun.

Existenz einer Umkehrfunktion

Die Umkehrfunktion existiert nur, wenn jeder Wert in der Wertemenge höchstens einmal "getroffen" wird (wenn jede Parallele zur x-Achse den Graphen der Funktion höchstens einmal schneidet).

Für die Funktion $f\left(x\right)=x^2$ rechts im Bild gibt es zwei Punkte auf der gleichen Höhe. Welchen Wert soll die Umkehrfunktion dem Wert $1$ zuordnen? Das ist nicht eindeutig, weshalb keine Umkehrfunktion auf der ganzen Definitionsmenge existiert.

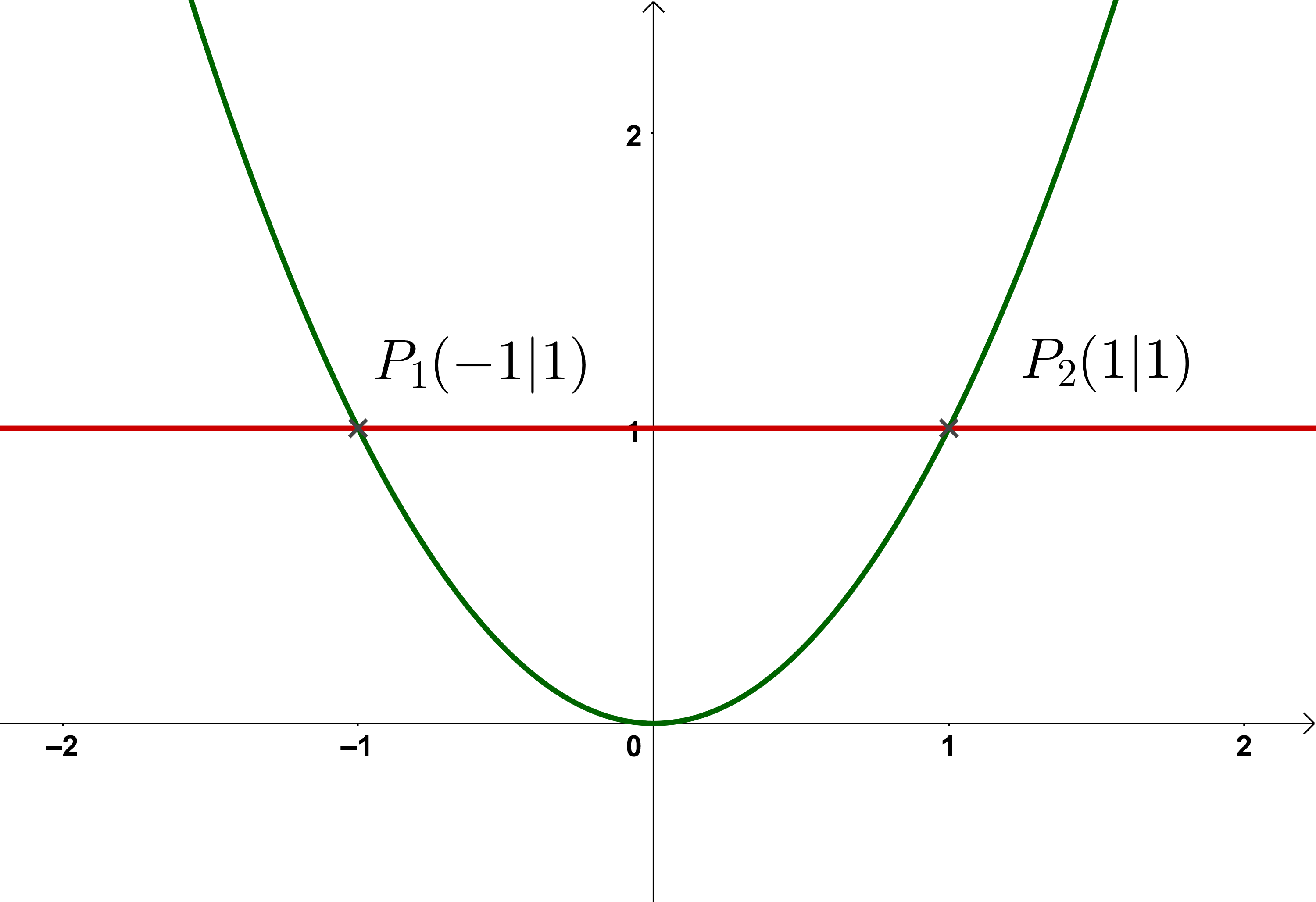
Das bedeutet: Werden bei einer Funktion die Werte aus der Wertemenge mehrmals "getroffen" (z. B. $f(x)=x^2$ , $g(x)=x^4$ , $h(x)=x^6$ ), muss man den Definitionsbereich so einschränken, dass sie jeden Wert aus der Wertemenge nur einmal "trifft". Anschließend kann man die Umkehrfunktion bilden.

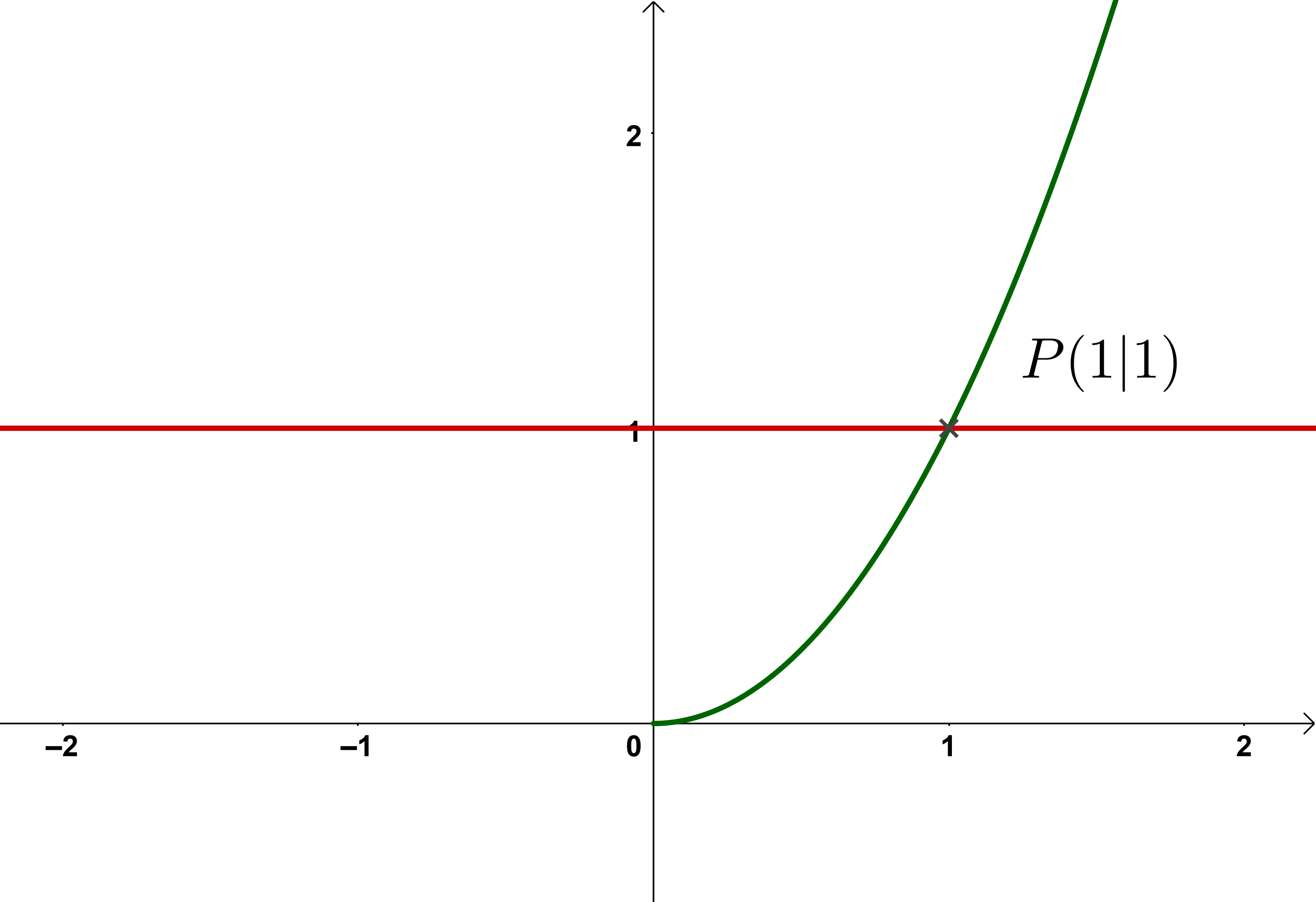
Der Definitionsbereich der Funktion wurde eingeschränkt, sodass jedem Wert der Definitionsmenge genau ein Wert der Wertemenge zugeordnet wird.

Das erkennt man daran, dass jede beliebige Parallele nur noch einen Schnittpunkt hat.

Die Umkehrfunktion von $f^{-1}$ ist wieder $f$ .

Definitions- und Wertemenge

Beim Umkehren vertauschen sich Definitions- und Wertemenge. Die Definitionsmenge von $f$ ist die Wertemenge von $f^{-1}$ und die Wertemenge von $f$ ist die Definitionsmenge von $f^{-1}$ .

Bilden der Umkehrfunktion

Im einfacheren Fall lässt sich die Gleichung $y=f(x)$ nach $x$ auflösen. Der Term auf der anderen Seite entspricht dann dem Funktionsterm der Umkehrfunktion.

Es gibt aber Fälle, in denen die Umkehrfunktion sich nicht finden lässt. Viele Funktionen werden aber auch direkt als Umkehrfunktionen definiert (siehe "Spezielle Umkehrfunktionen").

Beispiel

Bilden der Umkehrfunktion von

\displaystyle f:\;x\mapsto\frac1{x+2}-1

Bestimmen der Definitionsmenge: $D_f=ℝ\backslash\{-2\}; W_f=ℝ\backslash\{-1\}$

Nach x auflösen
	↓
$\displaystyle y$	$=$	$\displaystyle \frac{1}{x+2}-1$	$\displaystyle +1$
$\displaystyle y+1$	$=$	$\displaystyle \frac{1}{x+2}$	$\displaystyle \cdot\left(x+2\right)$
	↓	$\left\|{\cdot\left(x+2\right)}\right.$ ist erlaubt, da $-2\;\not\in\;D_f$ $\;\;\Rightarrow\;\;x+2\neq0$
$\displaystyle \left(y+1\right)\cdot\left(x+2\right)$	$=$	$\displaystyle 1$
	↓	$\left\|{:\left(y+1\right)}\right.$ Damit das erlaubt ist, muss $y+1\neq0$ $\Rightarrow-1\;\not\in\;W_f$
$\displaystyle x+2$	$=$	$\displaystyle \frac{1}{y+1}$	$\displaystyle -2$
$\displaystyle x$	$=$	$\displaystyle \frac{1}{y+1}-2$

$\;\;\Rightarrow\;\;f^{-1}(x)=\frac1{x+1}-2$

${\mathrm D}_{\mathrm f^{-1}}={\mathrm W}_\mathrm f=\mathbb{R}\backslash\{-1\};\;\;\;{\mathrm W}_{\mathrm f^{-1}}={\mathrm D}_\mathrm f=\mathbb{R}\backslash\{-2\}$

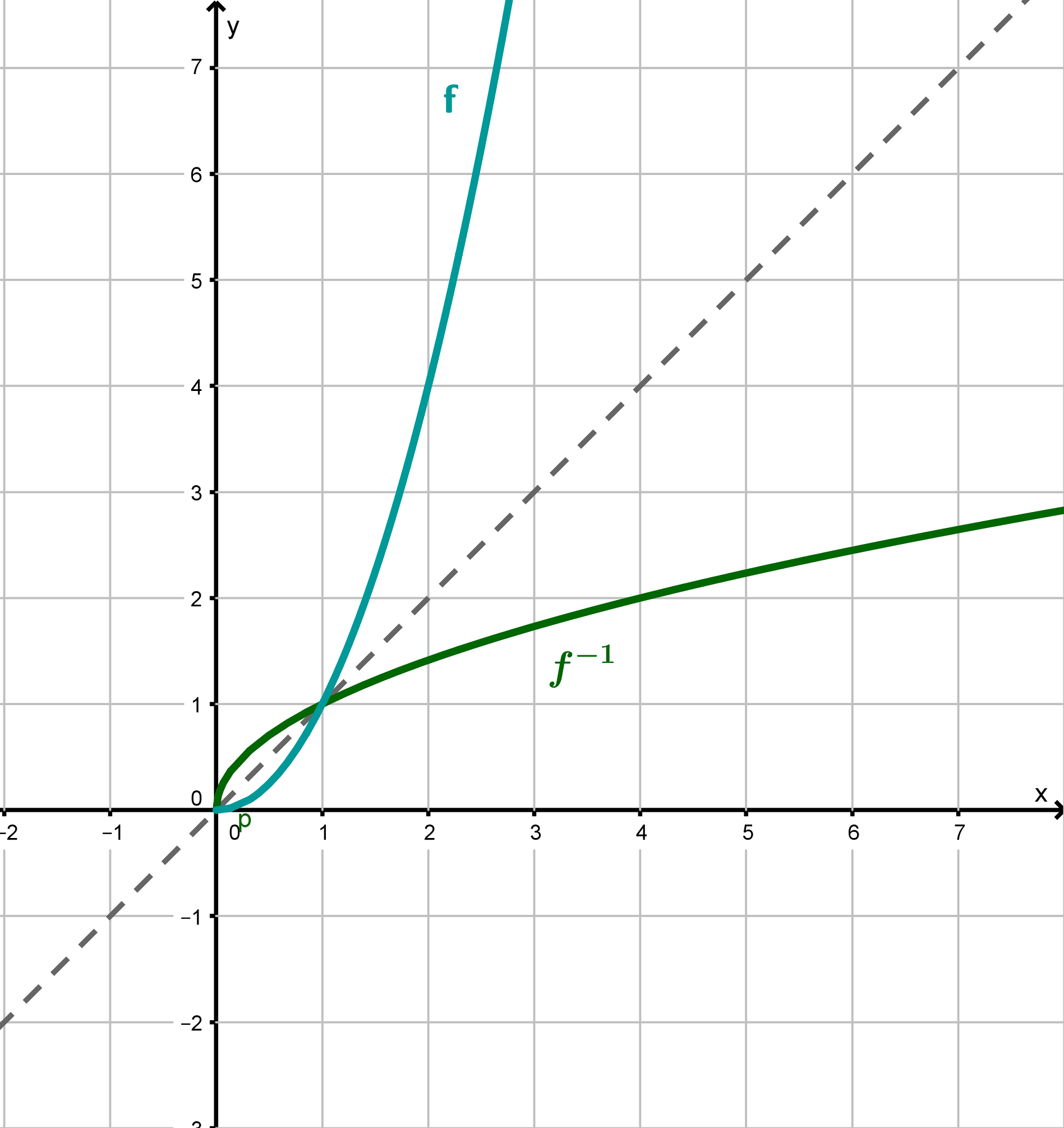
Graph der Umkehrfunktion

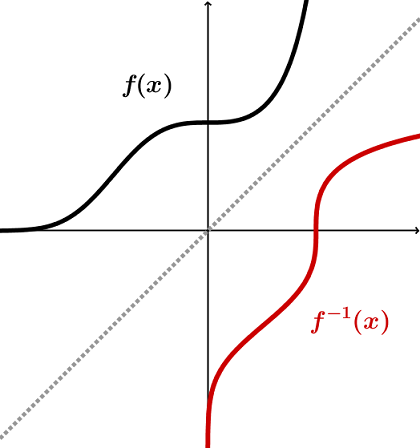
Umkehrfunktion als Spiegelung an der Winkelhalbierenden

Der Graph der Umkehrfunktion $f^{-1}$ ist der Graph von $f$ , gespiegelt an der Winkelhalbierenden des 1. und 3. Quadranten.

Spezielle Umkehrfunktionen

Die Funktion $f(x)=x$ ist ihre eigene Umkehrfunktion.
Die ln- und e-Funktion sind Umkehrfunktionen voneinander.
Die trigonometrischen Funktionen $\sin$ , $\cos$ , und $\tan$ müssen in ihrem Definitionsbereich eingeschränkt werden, um umkehrbar zu sein. Ihre Umkehrfunktionen sind der Arcus Sinus ( $\arcsin$ , oft auch $\sin^{-1}$ ), der Arcus Cosinus ( $\arccos$ bzw. $\cos^{-1}$ ) und der Arcus Tangens ( $\arctan$ bzw. $\tan^{-1}$ ).

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?