Aufgabe 4
In dieser Aufgabe geht es um Kerzen unterschiedlicher Form.
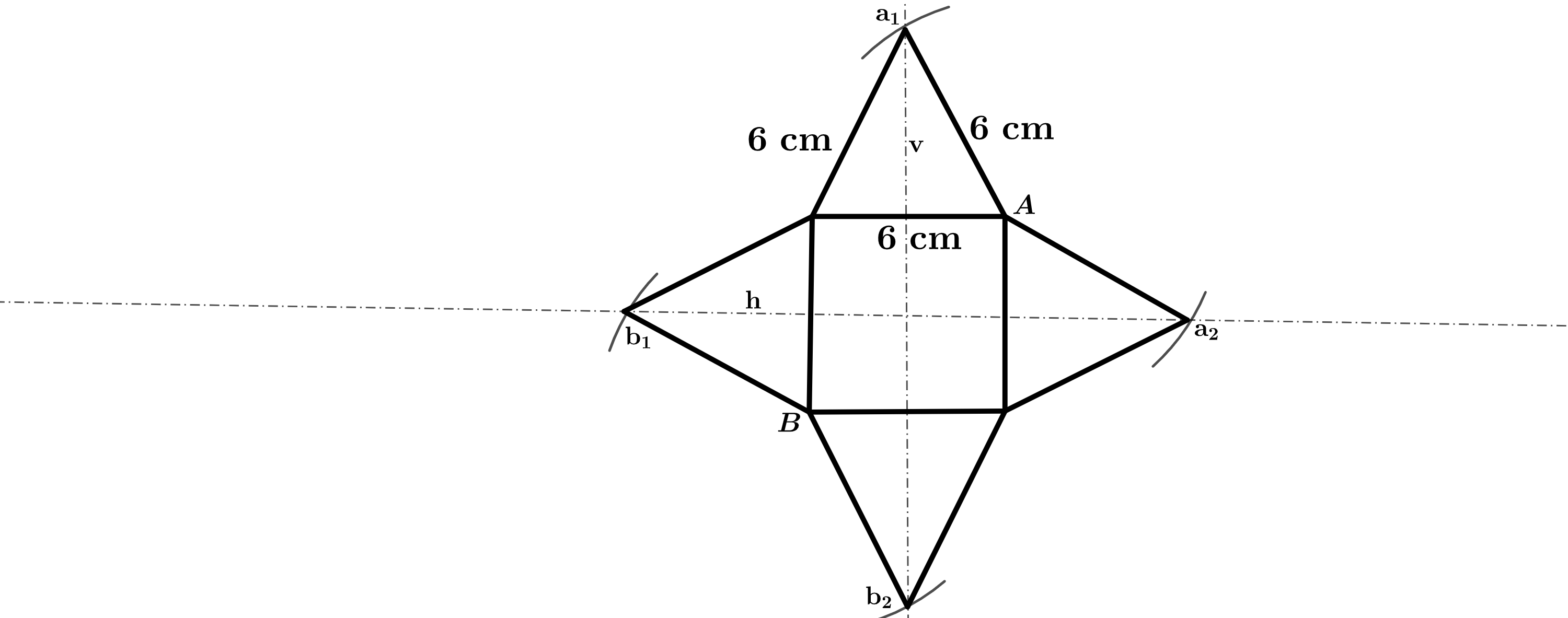
Eine Kerze hat die Form einer Pyramide, bei der alle Kanten lang sind.

Skizze nicht maßstabsgerecht
Zeichne ein Netz der Kerze im Maßstab . (3 BE)
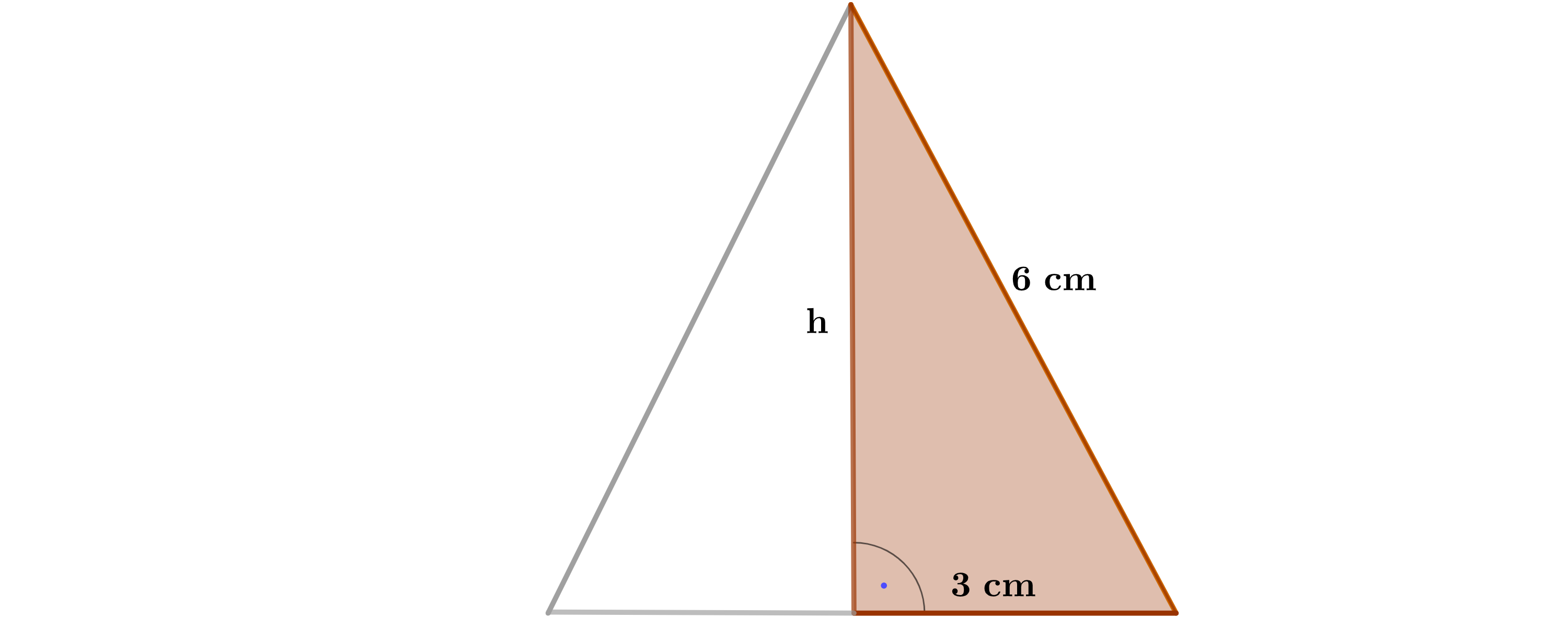
Berechne die Höhe einer Dreiecksseite der Kerze. (2 BE)
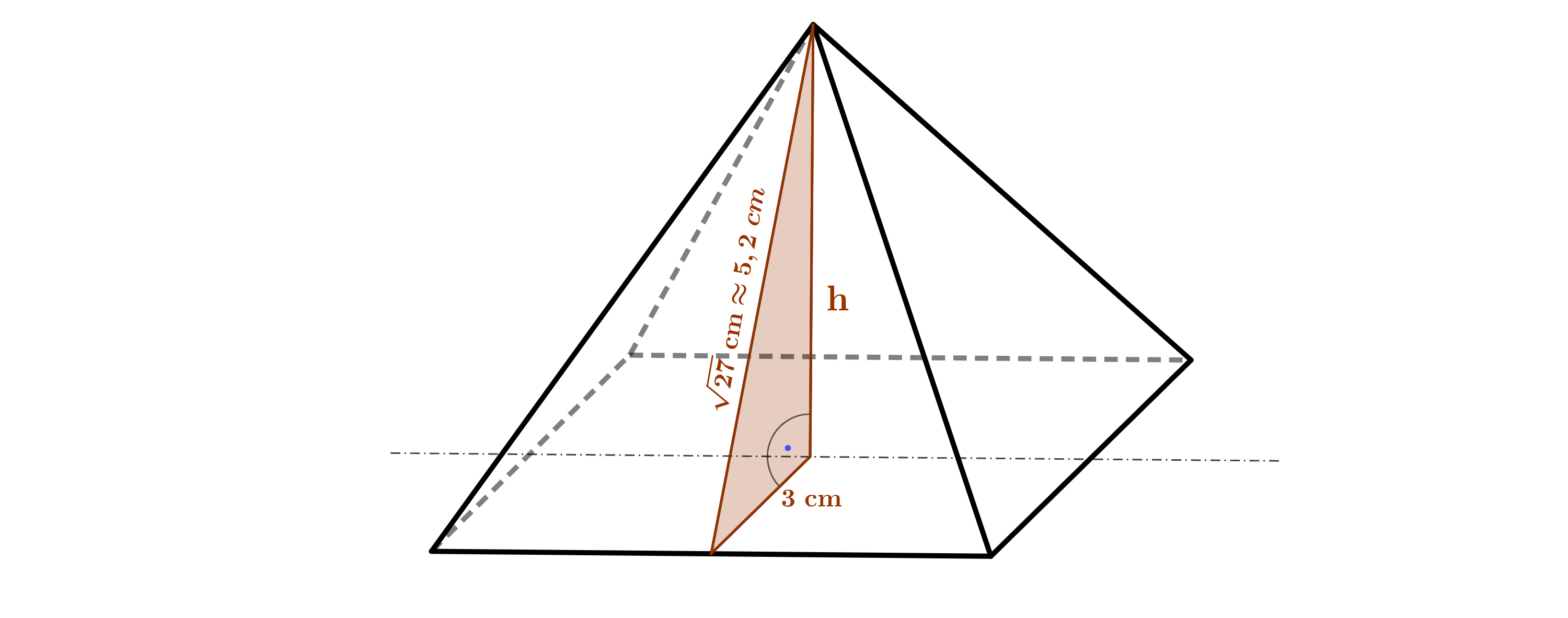
Berechne das Volumen der Kerze. (4 BE)
(Wenn du b) nicht gelöst hast, verwende .)
Skizze nicht maßstabsgerecht
Es soll eine Kerze in Form einer Kugel mit dem gleichen Volumen produziert werden.
Berechne den Radius dieser Kerze. (3 BE)
(Wenn du c) nicht gelöst hast, verwende .)
cmObwohl beide Kerzen das gleiche Volumen haben, sind die Oberflächen unterschiedlich groß. Die Oberfläche der kugelförmigen Kerze ist kleiner als die der pyramidenförmigen Kerze.
Berechne, um wie viel Prozent die Oberfläche der kugelförmigen Kerze kleiner ist. (4 BE)
(Wenn du d) nicht gelöst hast, verwende .)
In der Mitte der kugelförmigen Kerze ist ein Docht.
Aus Erfahrung weiß der Hersteller, dass die Kerze nur rund um den Docht abbrennt.
Das Kerzenwachs, das mehr als 1,6 cm vom Docht entfernt ist, bleibt stehen.
Es sollte nicht mehr als der Kerze nach dem Abbrennen übrig bleiben.
Überprüfe, ob bei der kugelförmigen Kerze die Vorgabe erfüllt wird. (4 BE)
Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen