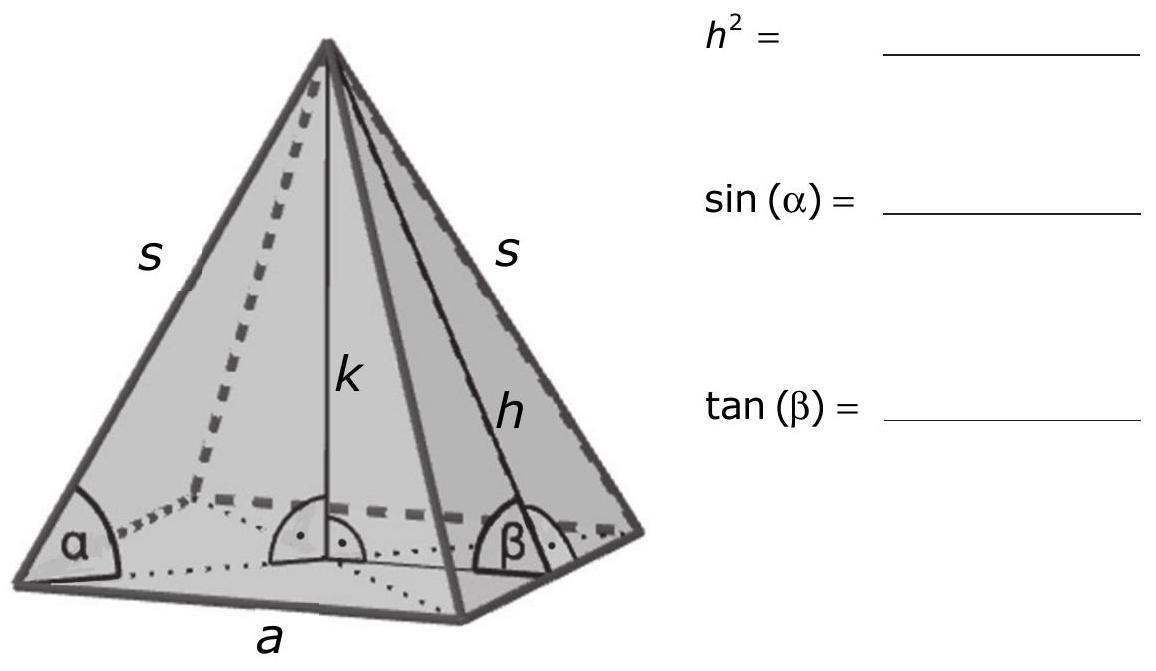
Gegeben ist eine regelmäßige Pyramide mit quadratischer Grundfläche. Ergänze die Formeln. (3 Punkte)
Dieses Werk wurde vom Ministerium für Allgemeine und Berufliche Bildung, Wissenschaft, Forschung und Kultur des Landes Schleswig-Holstein zur Verfügung gestellt.
serlo.orgDieses Werk wurde vom Ministerium für Allgemeine und Berufliche Bildung, Wissenschaft, Forschung und Kultur des Landes Schleswig-Holstein zur Verfügung gestellt.
→ Was bedeutet das?