Heft 1
🎓 Prüfungsbereich für Schleswig-Holstein
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Hier findest du die Aufgaben und Lösungen vom Prüfungsteil 1 des Mathe MSA 2023.
Ein Taschenrechner ist in diesem Prüfungsteil nicht erlaubt.
- 1
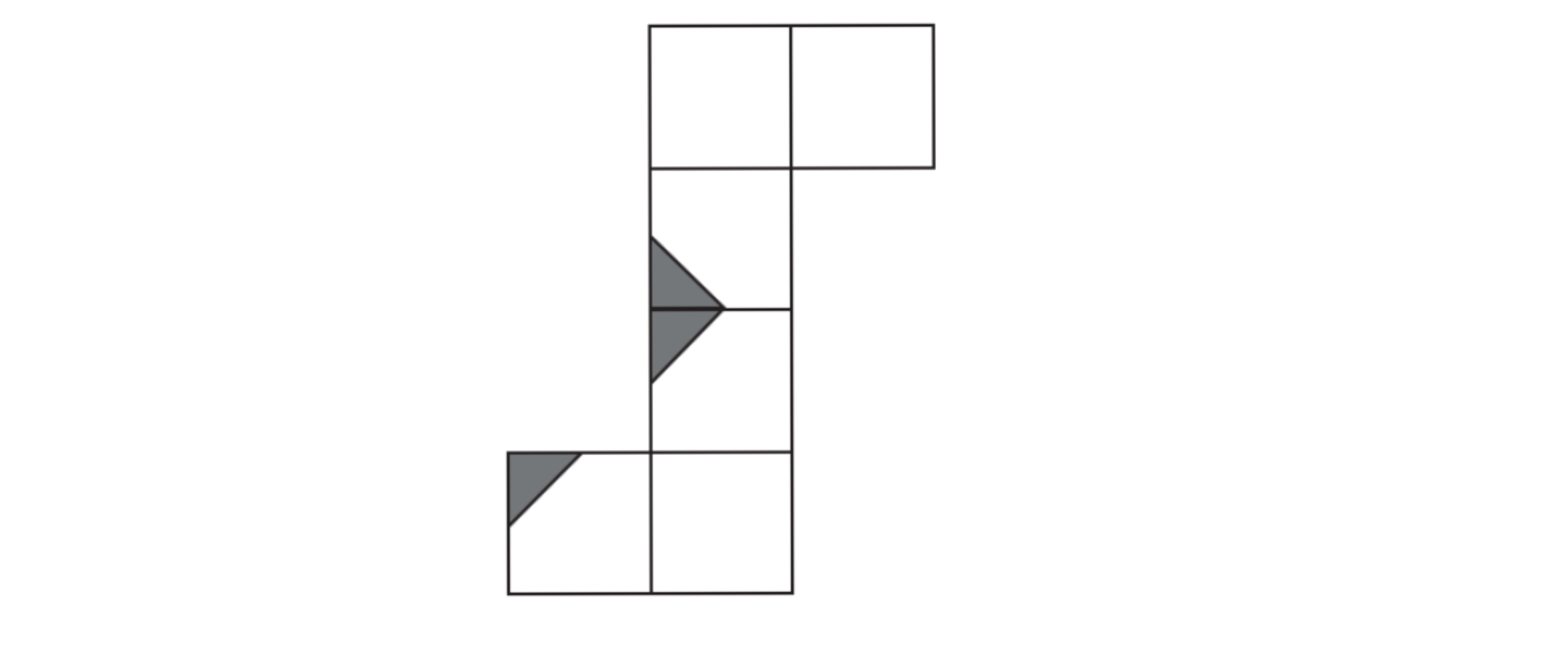
Der Würfel wurde an einer Ecke eingefärbt. Zeichne im Würfelnetz die zwei fehlenden farbigen Ecken ein. (1 Punkt)
- 2
In einem Gefäß befinden sich insgesamt 200 Lose. 20 Lose sind Gewinne, die anderen Lose sind Nieten. Die Lose werden ohne hinzusehen gezogen und nicht wieder zurückgelegt.
Wie groß ist die Wahrscheinlichkeit, dass das erste gezogene Los ein Gewinn ist? Kreuze an. (1 Punkt)
Aus den 200 Losen wurden 50 Nieten und kein Gewinn gezogen.
Welche Aussage trifft zu? Kreuze an. (1 Punkt)
- 3
- 4
Johanna hat ein Spiel für gekauft und dieses für an einen Freund verkauft.
Zeige, dass ihr Verlust beträgt. (1 Punkt)
- 5
Die Geraden und sind parallel. Gleiche Buchstaben bezeichnen gleich große Winkel. Gib die Größe der bezeichneten Winkel an. Die Abbildung ist nicht maßstabsgerecht. (2 Punkte)
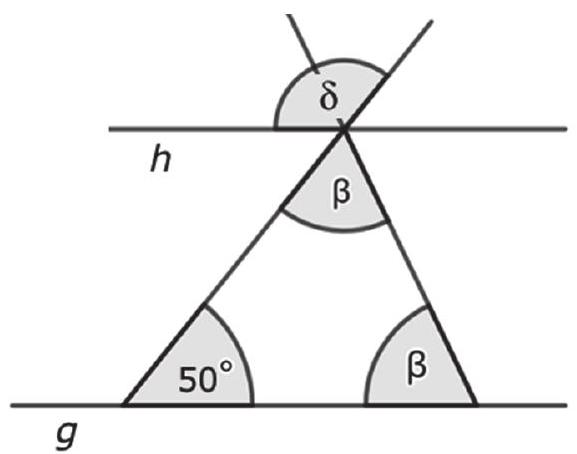
- 6
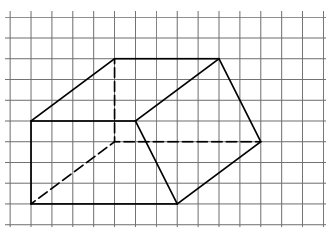
Ergänze das unvollständige Schrägbild des Trapezprismas. (1 Punkt)
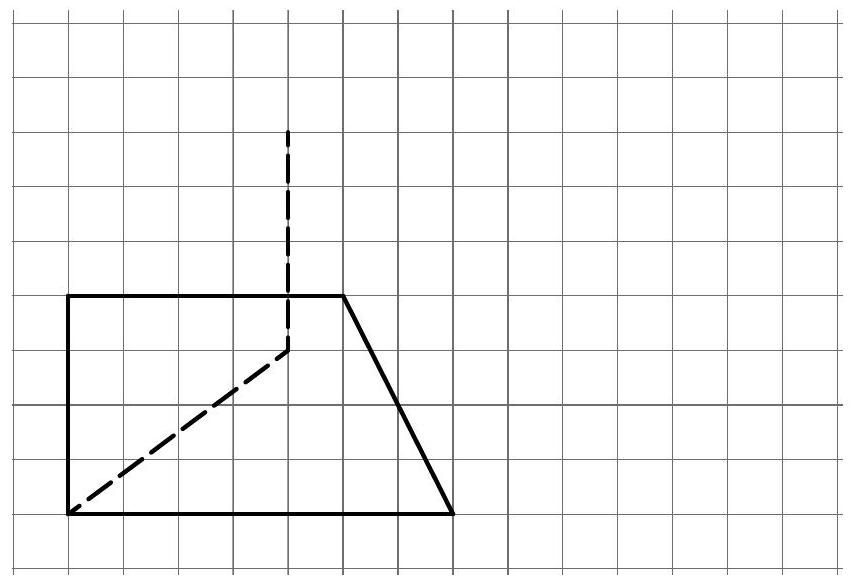
- 7
Widerlege jede Aussage, z.B. indem du ein Gegenbeispiel angibst.
Aussage: „Je größer eine natürliche Zahl ist, desto größer ist ihre Quersumme." (1 Punkt)
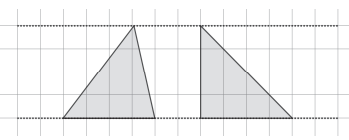
Aussage: "Wenn bei zwei Dreiecken die Längen der Grundseiten und die Längen der Höhen auf dieser Grundseite gleich sind, dann sind die Dreiecke kongruent." (1 Punkt)
- 8
In der ersten Reihe eines Theaters befinden sich 8 Plätze, in der zweiten Reihe befinden sich 10 Plätze, in der dritten Reihe 12 Plätze. Die Zunahme der Sitzplätze setzt sich in den weiteren Reihen genauso fort.
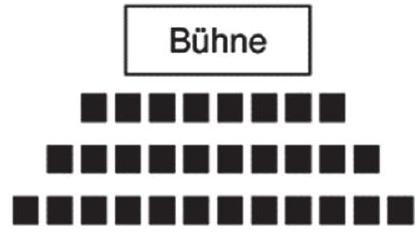
Wie viele Plätze befinden sich in Reihe 5? (1 Punkt)
Welcher Term gibt die Anzahl der Plätze in der -ten Reihe an? Kreuze den zutreffenden Term an. (1 Punkt)
- 9
Gegeben ist eine regelmäßige Pyramide mit quadratischer Grundfläche. Ergänze die Formeln. (3 Punkte)
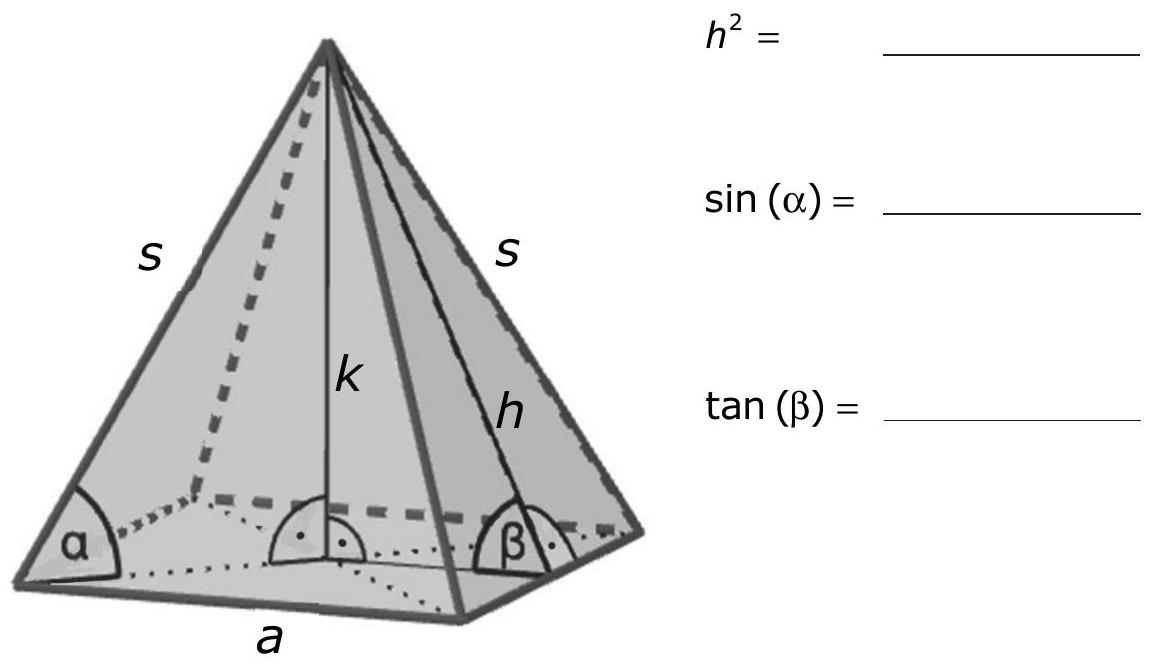
- 10
Bei beiden Divisoren fehlt ein Komma. Setze das Komma jeweils so, dass die Gleichung stimmt. (2 Punkte)
- 11
Gib den kleinsten und den größten Wert an: (2 Punkte)
- 12
Forme mithilfe einer binomischen Formel in ein Produkt um. (1 Punkt)
- 13
Ergänze jeweils so, dass die Gleichungen stimmen. (2 Punkte)
- 14
Gegeben ist die folgende quadratische Funktion in Normalform:
Welche der folgenden Funktionsgleichungen stellt diese Funktion in der Scheitelpunktform dar? Kreuze an. (1 Punkt)
- 15
Verbinde jedes der drei Beispiele links mit dem passenden Begriff rechts. (3 Punkte)
Du kannst die Worte rechts mit der Maus ziehen.
- 16
Wahr oder falsch? Kreuze jeweils an. (3 Punkte)
- 17
Soraya hat auf die Seitenflächen eines Würfels die Zahlen -5, - 3, - 1, 2, 4, 6 geschrieben. Sie würfelt mit diesem Würfel zweimal hintereinander und addiert die beiden gewürfelten Zahlen. Welche Summe kann sie nicht erhalten? (1 Punkt)
- 18
In einem Beutel befinden sich fünf Kugeln: 2 grüne und 3 blaue
Es werden zwei grüne Kugeln gezogen, die nicht wieder zurückgelegt werden. Wie groß ist die Wahrscheinlichkeit beim nächsten Zug eine blaue Kugel zu ziehen? Kreuze an. (1 Punkt)
Es wird dreimal gezogen und die Kugeln werden nicht wieder zurückgelegt. Mit welchem Term lässt sich die Wahrscheinlichkeit berechnen alle blauen Kugeln zu ziehen? Kreuze an. (1 Punkt)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?