Teil 2, Stochastik 2 - lernen mit Serlo!

In einer Gärtnerei werden drei Blumenarten gezüchtet und verkauft. Es handelt sich dabei um Tulpen ( $\mathrm{T}$ ), Osterglocken (O) und Krokusse (K). Während Krokusse ausschließlich aus Blumenzwiebeln (B) und Osterglocken ausschließlich aus Samen (S) gezüchtet werden, werden Tulpen sowohl aus Blumenzwiebeln als auch aus Samen erzeugt. Von allen drei Blumenarten werden gelbe ( $\mathrm{g}$ ) und weiße (w) zum Verkauf angeboten.

Die Hälfte aller verkauften Blumen sind Tulpen. Die beiden anderen Blumensorten werden jeweils zu gleichen Anteilen verkauft. Die aus Samen wachsenden Tulpen haben unter dieser Blumenart einen Verkaufsanteil von $40 %$ . Unabhängig von Blumensorte und Züchtungsform werden $75 %$ aller verkauften Blumen mit der Farbe Gelb gewählt.

Der Kauf einer Blume hinsichtlich ihrer Eigenschaften Blumenart, Züchtungsform und Farbe wird im Folgenden als Zufallsexperiment mit entsprechenden Wahrscheinlichkeiten betrachtet.

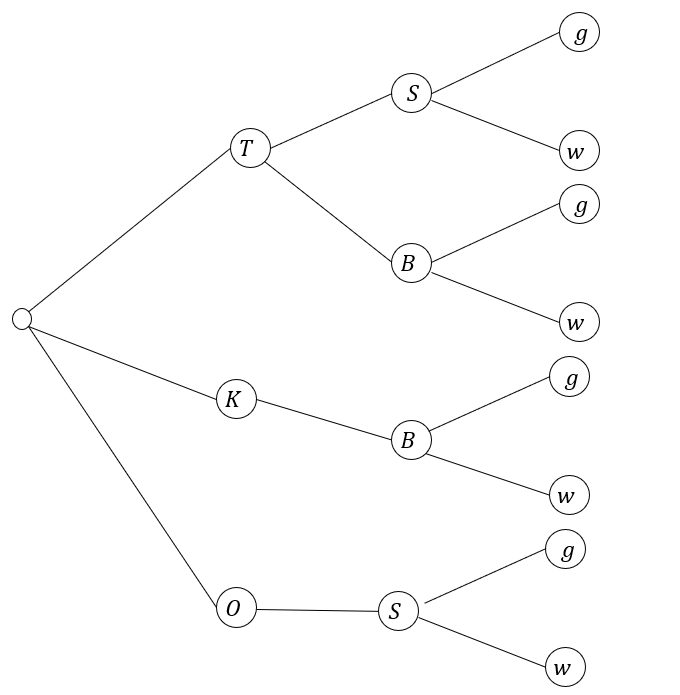
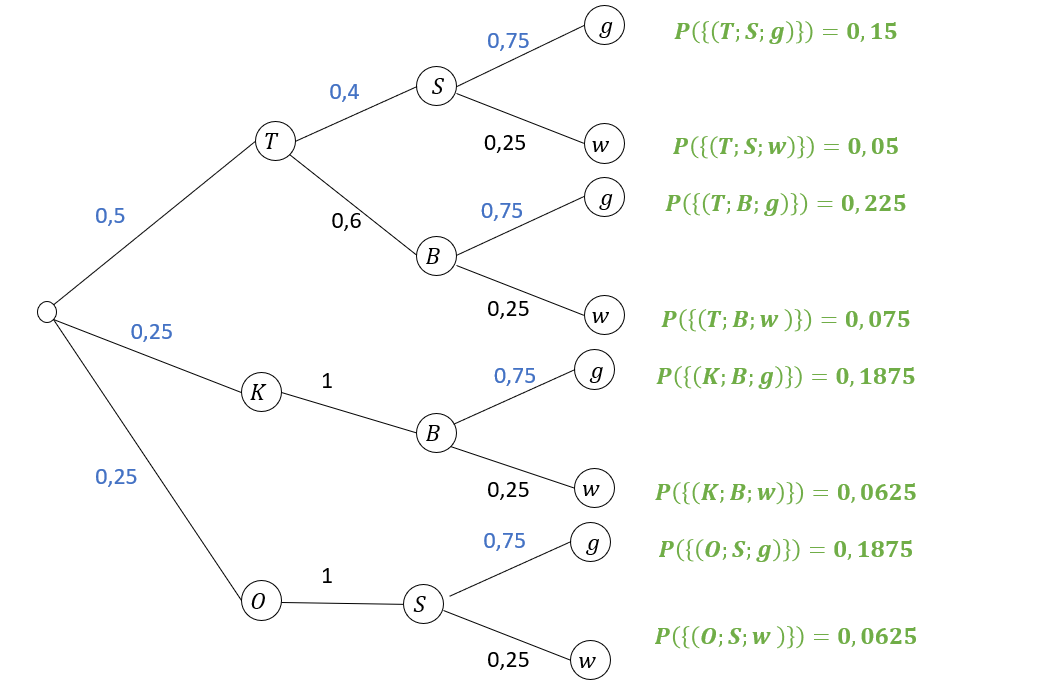
Erstellen Sie für das vorliegende Zufallsexperiment ein Baumdiagramm und ermitteln Sie alle acht Elementarereignisse mit ihren Wahrscheinlichkeiten.
[ Teilergebnis: $\mathrm{P}(\{(\mathrm{T} ; \mathrm{B} ; \mathrm{g})\})=0{,}225$ ]
(5 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm und Pfadregeln
Struktur des Baums
Da nicht jede Blumenart aus jeder Züchtungsform hervorgeht, ist der Baum nicht ganz gleichmäßig:
Wahrscheinlichkeiten
Ergänze zuerst alle Wahrscheinlichkeiten aus der Aufgabenstellung (blau im Baum) und berechne dann die anderen Wahrscheinlichkeiten im Baum (schwarz) sowie die Wahrscheinlichkeiten der Elementarereignisse (grün).
Hinweise zum Baumdiagramm:
"restliche Blumen zu gleichen Teilen": Krokusse und Osterglocken jeweils 25%
"Unabhängig von Blumensorte und Züchtungsform": Alle Pfade zu g haben 75% Wahrscheinlichkeit
Gibt es nur einen Pfad, ist die Wahrscheinlichkeit für diesen 100%=1
Berechne die Wahrscheinlichkeiten der Elementarereignisse mit der 1. Pfadregel, z.B. $P(\{(T;S;g)\})=0{,}5\cdot0{,}4\cdot0{,}75=0{,}15$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Überlege dir die Struktur des Baumdiagramms, zum Beispiel mithife des Elementarereignis (T;B;g) aus dem Teilergebnis
Lese möglichst viele Wahrscheinlichkeiten aus der Aufgabenstellung
Berechne die übrigen Wahrscheinlichkeiten, zum Beispiel mit den Pfadregeln
Nun werden folgende Ereignisse betrachtet:
$E_{1} :$ „Die verkaufte Blume ist gelb und ist keine Tulpe.“
$\mathrm{E}_{2}=\{(\mathrm{T} ; \mathrm{S} ; \mathrm{g}) ;(\mathrm{T} ; \mathrm{S} ; \mathrm{w}) ;(\mathrm{O} ; \mathrm{S} ; \mathrm{g}) ;(\mathrm{O} ; \mathrm{S} ; \mathrm{w})\}$
Geben Sie $E_{1}$ in aufzählender Mengenschreibweise an und formulieren Sie $E_{2}$ möglichst einfach im Sachzusammenhang. Berechnen Sie anschließend $P\left(E_{2}\right)$ .
(3 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Mengenlehre
$E_{1}$ in aufzählender Mengenschreibweise
Entnehme dem Baum alle Pfade, bei denen die Blume gelb ist, aber keine Tulpe:
$E_1=\{(K;B;g);(O;S;g)\}$
$E_{2}$ in Worten und $P (E_{2})$
Das mittlere Element in den Elementarereignissen ist immer ein S:
Die Blume wurde aus Samen gezüchtet.
Addiere nun alle benötigten grünen Wahrscheinlichkeiten aus der letzten Teilaufgabe:
$P(E_2)=P(\{(T;S;g\})+P(\{(T;S;w\})+P(\{(O;S;g\})+P(\{(O;S;w\})=0{,}15+0{,}05+0{,}1875+0{,}0625=0{,}45$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Für die Mengenschreibweise: Wähle aus dem Baum alle Elementarereignisse aus, die der Beschreibung von $E_{1}$ genügen und gib sie in der Form wie $E_{2}$ an.
Für die Formulierung von $E_{2} :$ Suche nach Gemeinsamkeiten und Unterschieden bei den enthaltenen Elementen
Für die Wahrscheinlichkeit: Verwende die 2. Pfadregel, um alle Wahrscheinlichkeiten der gesuchten Elementarereignisse aus dem letzten Schritt zu verrechnen.

Struktur des Baums

Wahrscheinlichkeiten

Hast du eine Frage oder Feedback?

E1E_1E1​ in aufzählender Mengenschreibweise

E2E_2E2​ in Worten und P(E2)P(E_2)P(E2​)

Hast du eine Frage oder Feedback?

$E_{1}$ in aufzählender Mengenschreibweise

$E_{2}$ in Worten und $P (E_{2})$