Teil 2, Stochastik 2

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellungen zum Ausdrucken findest du hier als PDF.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
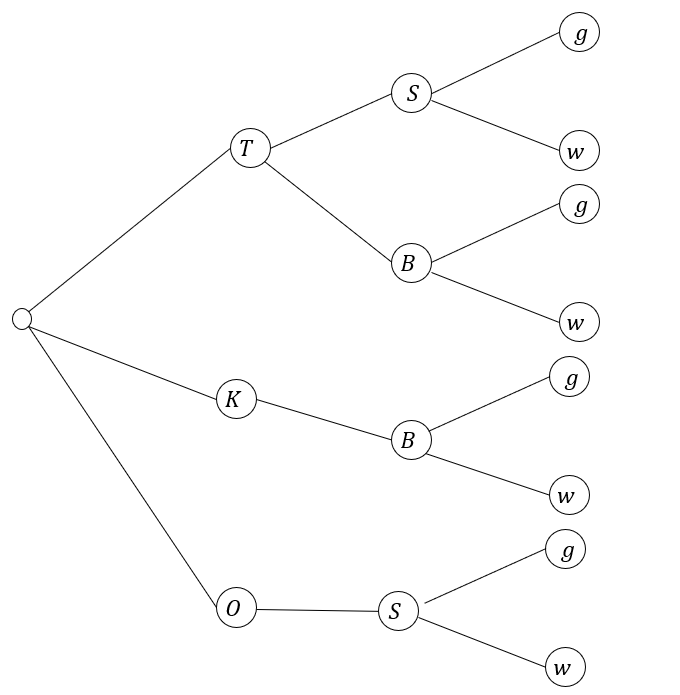
In einer Gärtnerei werden drei Blumenarten gezüchtet und verkauft. Es handelt sich dabei um Tulpen ( $\mathrm{T}$ ), Osterglocken (O) und Krokusse (K). Während Krokusse ausschließlich aus Blumenzwiebeln (B) und Osterglocken ausschließlich aus Samen (S) gezüchtet werden, werden Tulpen sowohl aus Blumenzwiebeln als auch aus Samen erzeugt. Von allen drei Blumenarten werden gelbe ( $\mathrm{g}$ ) und weiße (w) zum Verkauf angeboten.
Die Hälfte aller verkauften Blumen sind Tulpen. Die beiden anderen Blumensorten werden jeweils zu gleichen Anteilen verkauft. Die aus Samen wachsenden Tulpen haben unter dieser Blumenart einen Verkaufsanteil von $40 \%$ . Unabhängig von Blumensorte und Züchtungsform werden $75 \%$ aller verkauften Blumen mit der Farbe Gelb gewählt.
Der Kauf einer Blume hinsichtlich ihrer Eigenschaften Blumenart, Züchtungsform und Farbe wird im Folgenden als Zufallsexperiment mit entsprechenden Wahrscheinlichkeiten betrachtet.
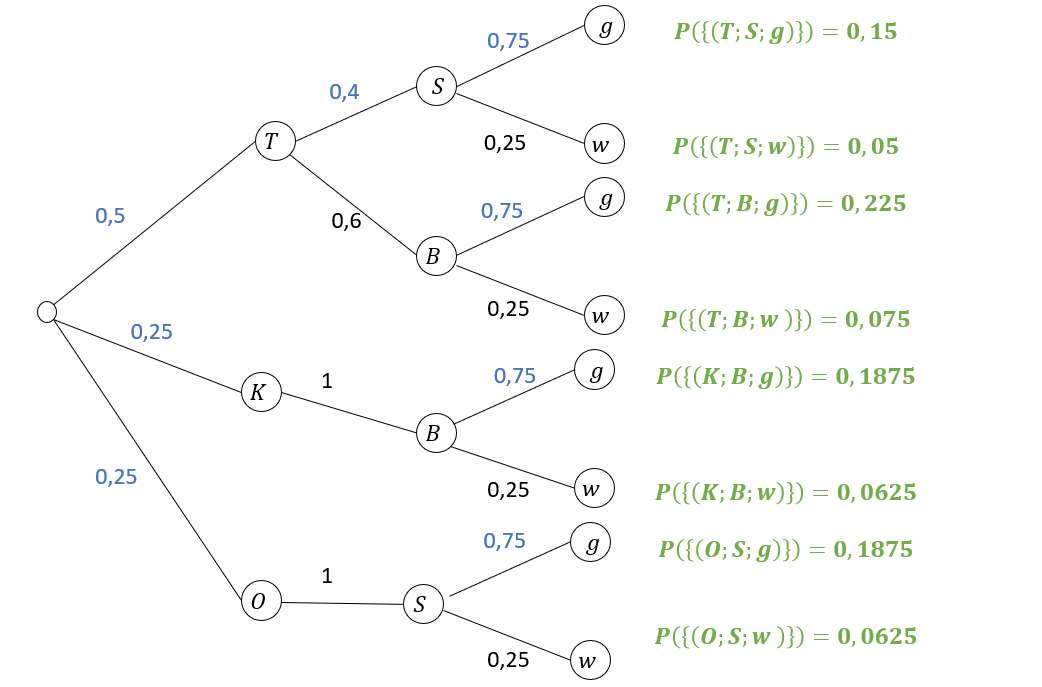
1. Erstellen Sie für das vorliegende Zufallsexperiment ein Baumdiagramm und ermitteln Sie alle acht Elementarereignisse mit ihren Wahrscheinlichkeiten.
  [ Teilergebnis: $\mathrm{P}(\{(\mathrm{T} ; \mathrm{B} ; \mathrm{g})\})=0{,}225$ ]
  (5 BE)
2. Nun werden folgende Ereignisse betrachtet:
  $E_{1}:$ „Die verkaufte Blume ist gelb und ist keine Tulpe.“
  $\mathrm{E}_{2}=\{(\mathrm{T} ; \mathrm{S} ; \mathrm{g}) ;(\mathrm{T} ; \mathrm{S} ; \mathrm{w}) ;(\mathrm{O} ; \mathrm{S} ; \mathrm{g}) ;(\mathrm{O} ; \mathrm{S} ; \mathrm{w})\}$
  Geben Sie $E_{1}$ in aufzählender Mengenschreibweise an und formulieren Sie $E_{2}$ möglichst einfach im Sachzusammenhang. Berechnen Sie anschließend $P\left(E_{2}\right)$ .
  (3 BE)
2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Im Gewächshaus der Gärtnerei werden in einem neu angelegten Beet 30 Tulpenzwiebeln nebeneinander eingesetzt. Mit einer Wahrscheinlichkeit von $p=0{,}85$ geht eine eingesetzte Tulpenzwiebel tatsächlich auf und es wächst daraus eine Tulpe.
1. Bestimmen Sie die Wahrscheinlichkeit, dass aus genau 25 der eingesetzten Zwiebeln Tulpen entstehen. (2 BE)
2. Ermitteln Sie die Wahrscheinlichkeit des Ereignisses $\mathrm{E}_{3}:$ "Genau zwei der Zwiebeln gehen nicht auf und diese wurden direkt nebeneinander eingesetzt.“ (2 BE)
3. Berechnen Sie die Wahrscheinlichkeit, dass aus mindestens 29 der eingesetzten Zwiebeln Tulpen entstehen. Entscheiden Sie begründet, ob die folgende Aussage für alle Werte von k mit $1 \leq k \leq 29$ wahr ist:
  „Die Wahrscheinlichkeit, dass aus 30 eingesetzten Tulpenzwiebeln mindestens k Tulpen entstehen, liegt nicht unter $4 \%$ ." (4 BE)
3
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Für eine Zufallsgröße $X$ ist die Wahrscheinlichkeitsverteilung mit $a, b \in \mathbb{R}$ durch folgende Tabelle vollständig gegeben:
x
0
1
2
3
4
5
P(X=x)
a
2b
b
0,1
0,1
0,04
1. Bestimmen Sie die Werte der Parameter $a$ und $b$ , wenn der Erwartungswert von $X$ gleich 1,7 ist.
  [ Teilergebnis: $b=0{,}2$ ]
  (3 BE)
2. Die Blumensorte Tulpe erzeugt während ihres Wachstums sogenannte Tochterzwiebeln, die ihrerseits wieder zur Entstehung weiterer Tulpen führen. Die unter 3.0 aufgeführte Wahrscheinlichkeitsverteilung mit den unter Aufgabe 3.1 bestimmten Werten für a und b gibt an, welche Anzahl von Tochterzwiebeln mit welcher Wahrscheinlichkeit auftritt.
  Berechnen Sie, mit welcher Wahrscheinlichkeit die Zufallswerte von $X$ innerhalb der einfachen Standardabweichung um den Erwartungswert liegen. (4 BE)

x	0	1	2	3	4	5
P(X=x)	a	2b	b	0,1	0,1	0,04

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?