Berechnest du eine kumulierte Wahrscheinlichkeit, so summierst du die Wahrscheinlichkeit mehrerer Ereignisse auf.
Meist wird die kumulierte Wahrscheinlichkeit bei binomialverteilten Zufallsgrößen und den zugehörigen Bernoulli-Ketten verwendet, um statt auch Wahrscheinlichkeiten der Form und alle Variationen von zu bestimmen.
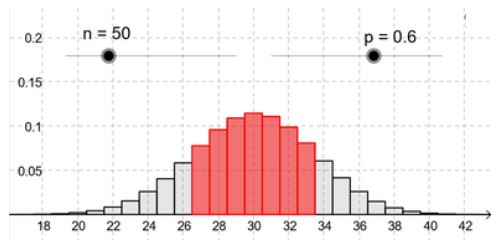
Die Binomialverteilung bei und . Der rot markierte Bereich ist die kumulierte Wahrscheinlichkeit .
Berechnung der kumulierten Wahrscheinlichkeit ohne besondere Hilfsmittel
Um eine kumulierte Wahrscheinlichkeit zu bestimmen, addierst du die Wahrscheinlichkeiten aller Teilereignisse im vorgegebenen Bereich.
bedeutet zum Beispiel, dass die Zufallsgröße die Werte , und annehmen kann. Die zugehörige Wahrscheinlichkeit ergibt sich also aus:
Das Unternehmen Nesla stellt Elektrofahrzeuge her. Leider ist der Hersteller noch sehr unerfahren und produziert ab und zu fehlerhafte Produkte. Die Wahrscheinlichkeit beträgt , dass ein Auto Fehler aufweist.
Wir berechnen die kumulierte Wahrscheinlichkeit, dass in einer Lieferung von Fahrzeugen, höchstens defekt sind.
Kumulierte Wahrscheinlichkeit besteht aus einzelnen Wahrscheinlichkeiten | |||
| ↓ | |||
| ↓ | Die Wahrscheinlichkeit hier ist binomialverteilt zu , | ||
| ↓ | Das liefert uns der Taschenrechner | ||
Die Wahrscheinlichkeit ist ungefähr , dass höchstens 4 defekte Fahrzeuge dabei sind.
Aufwändigere kumulierte Wahrscheinlichkeiten
Während du beim ersten Beispiel die drei Teilwahrscheinlichkeiten vielleicht noch schnell mit der Bernoulli-Formel berechnest, hast du bei eher weniger Spaß, denn du müsstest alle Teilwahrscheinlichkeiten aufsummieren. Oder kurz geschrieben mit dem Summenzeichen: .
Hier helfen dir stochastische Tabellen, wie zum Beispiel das Tafelwerk oder der Geogebra Wahrscheinlichkeitsrechner. Auch manche Taschenrechner können das berechnen, schau in der Bedienungsanleitung nach.
Gedruckte Tabellen (die du meistens in der Schule verwenden musst) haben dabei eine Einschränkung: lediglich Wahrscheinlichkeiten der Form können nachgeschaut werden. Im Tafelwerk ist dies zum Beispiel die rechte Spalte der Tabelle. Alle anderen Fälle musst du umschreiben:
zu bestimmende Wahrscheinlichkeit | in Worten | so muss sie umgeschrieben werden | gefragter Bereich am Zahlenstrahl (orange ist jeweils der gefragte Bereich) |
|---|---|---|---|
höchstens k Treffer | (kann direkt nachgeschaut werden) |  | |
weniger als k Treffer |
(einen Wert davor nachschauen) |  | |
mindestens k Treffer | (Gegenereignis betrachten) |  | |
mehr als k Treffer | (Gegenereignis betrachten) |  | |
mehr als aber höchstens Treffer | (Bereich bis zu muss wieder weggenommen werden |  | |
Alle anderen Fälle mit und | (Kombination aus den obigen) | Auf zurückführen | (analog zum oberen Bild mit anderen Grenzen) |
Berechnung mit dem Taschenrechner
Die Berechnung einer kumulierten Wahrscheinlichkeit, gerade bei der Binomialverteilung, ist von Hand sehr mühsam. Die meisten Taschenrechner oder Online-Rechner haben eine Funktion BinomialCDF oder PoissonCDF etc. Wo diese zu finden ist, steht in der Betriebsanleitung. Damit lassen sich kumulierte Wahrscheinlichkeiten von der Form in einem Schritt berechnen.
Im Beispiel unseres Automobilherstellers können wir berechnen:
BinomialCDF mit | |||
| ↓ | |||
Ein weiterer Kunde gibt Fahrzeuge in Auftrag, droht aber den Vertrag zu kündigen, sobald mehr als 3 Fahrzeuge defekt sind.
Berechne .
Das ist das Gegenereignis, siehe unten. | |||
| ↓ | |||
| ↓ | BinomialCDF mit | ||
Die Wahrscheinlichkeit, dass mehr als 3 Fahrzeug kaputt sind, liegt bei ungefähr . Damit springt der Kunde recht sicher vom Vertrag ab.
