Standardabweichung

Die Standardabweichung $\sigma$ (Sigma) einer Zufallsgröße ist in der Stochastik ein Maß dafür, wie stark im Mittel die Zufallsgröße um ihrem Erwartungswert streut. Sie ist eng mit der Varianz verknüpft.

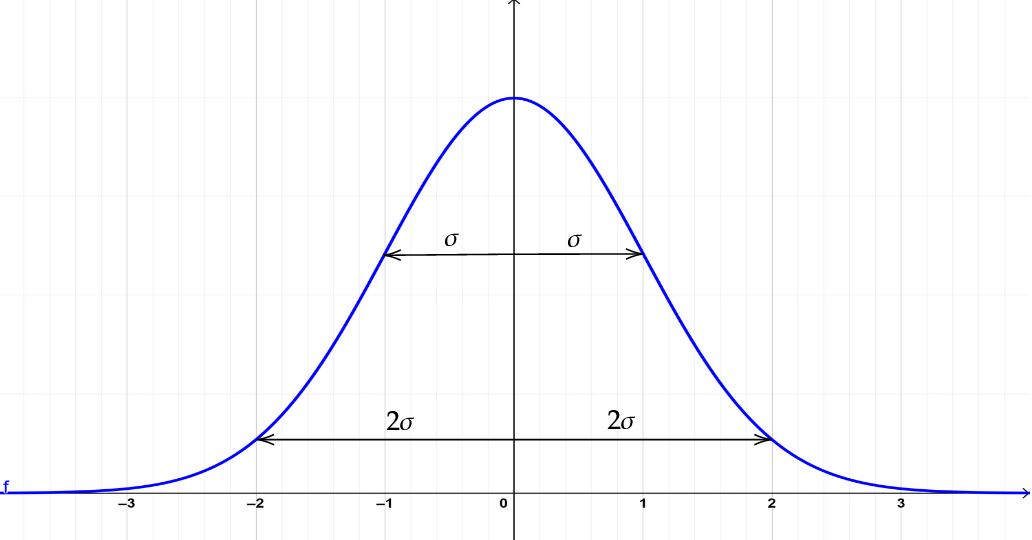
Darstellung der Standardabweichung für die Standardnormalverteilung.

Berechnung

Die Standardabweichung $\sigma(X)$ einer Zufallsvariablen X ist definiert als die Quadratwurzel der Varianz $Var(X)$ :

$\sigma(X)=\sqrt{V(X)}$

Wichtige Standardabweichungen

Verteilungen	Varianz	Standardabweichung
Bernoulli-Verteilung	$p\;\cdot\;(1- p)$	$\sqrt{p\cdot (1-p)}$
Binomialverteilung	$\; n\;\cdot\; p\;\cdot\;(1- p)$	$\sqrt{\; n\;\cdot\; p\;\cdot\;(1- p)}$
Normalverteilung	$X\sim N\left(\mu\;,\;\sigma^2\right)\;\Rightarrow\;\sigma^2$	$\sigma$

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel

Zufallsgröße
Verteilungsfunktion
Varianz
Erwartungswert

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?