Teil 1 Lineare Algebra - lernen mit Serlo!

In einem kartesischen Koordinatensystem des $ℝ^{2}$ ist je ein Repräsentant der Vektoren $\vec{a}$ und $\vec{b}$ gegeben.

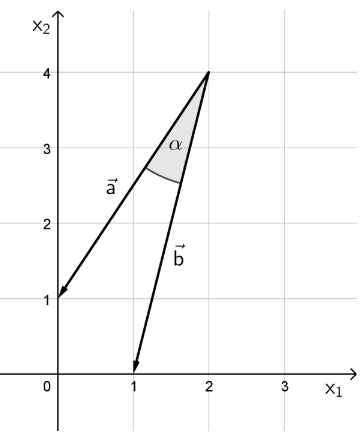
Der Winkel $α$ zwischen den beiden Vektoren $\vec{a}$ und $\vec{b}$ kann mit der Gleichung
$c o s (α) = \frac{\vec{a} \circ \vec{b}}{| \vec{a} | \cdot | \vec{b} |}$ berechnet werden. In einer der drei nachfolgenden Gleichungen ist der Term $\frac{\vec{a} \circ \vec{b}}{| \vec{a} | \cdot | \vec{b} |}$ richtig berechnet. Entscheiden Sie begründet, welche der untenstehenden Gleichungen die richtige ist.
- $c o s (α) = \frac{12}{\sqrt{13} \cdot \sqrt{18}}$
- $c o s (α) = \frac{14}{\sqrt{13} \cdot \sqrt{17}}$
- $c o s (α) = \frac{14}{\sqrt{3} \cdot \sqrt{5}}$
Zeichnen Sie einen Repräsentanten des Vektors $\vec{c} = \vec{a} - \vec{b}$ in das Koordinatensystem der Aufgabenstellung ein.
Zeigen Sie rechnerisch, dass die Vektoren $\vec{a}$ und $\vec{b}$ linear unabhängig sind.