Teil 1 Lineare Algebra

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgaben zum Ausdrucken als PDF findest du hier

Die Aufgaben in diesem Ordner sollen ohne Hilfsmittel wie Taschenrechner oder Formelsammlung bearbeitet werden.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
In einem kartesischen Koordinatensystem des $ℝ^{2}$ ist je ein Repräsentant der Vektoren $\vec{a}$ und $\vec{b}$ gegeben.
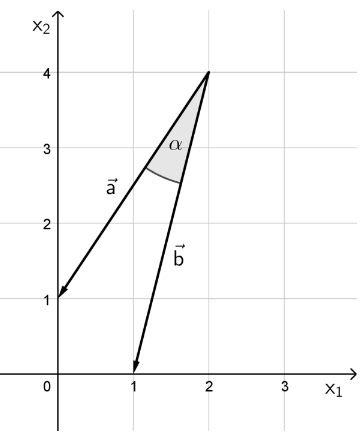
1. Der Winkel $α$ zwischen den beiden Vektoren $\vec{a}$ und $\vec{b}$ kann mit der Gleichung
  $c o s (α) = \frac{\vec{a} \circ \vec{b}}{| \vec{a} | \cdot | \vec{b} |}$ berechnet werden. In einer der drei nachfolgenden Gleichungen ist der Term $\frac{\vec{a} \circ \vec{b}}{| \vec{a} | \cdot | \vec{b} |}$ richtig berechnet. Entscheiden Sie begründet, welche der untenstehenden Gleichungen die richtige ist.
  $c o s (α) = \frac{12}{\sqrt{13} \cdot \sqrt{18}}$
  $c o s (α) = \frac{14}{\sqrt{13} \cdot \sqrt{17}}$
  $c o s (α) = \frac{14}{\sqrt{3} \cdot \sqrt{5}}$
2. Zeichnen Sie einen Repräsentanten des Vektors $\vec{c} = \vec{a} - \vec{b}$ in das Koordinatensystem der Aufgabenstellung ein.
3. Zeigen Sie rechnerisch, dass die Vektoren $\vec{a}$ und $\vec{b}$ linear unabhängig sind.
2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
In einem kartesischen Koordinatensystem des $ℝ^{3}$ sind die drei Punkte $A (2 | 0 | 0)$ , $B (5 | 0 | 0)$ und $C (4 | 1 | - 1)$ gegeben.
1. Zeigen Sie, dass der Winkel an der Ecke $C$ im Dreieck $A B C$ ein rechter Winkel ist.
2. Berechnen Sie die Maßzahl des Flächeninhalts des Dreiecks $A B C .$

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?