Teil 1 Analysis - lernen mit Serlo!

Gegeben ist die Funktion $p$ durch $p (x) = \frac{x^{2} - 1}{4 - x^{2}}$ mit ihrer maximalen Definitionsmenge $D_{p} = ℝ$ $∖ {- 2; 2}$ . Der Graph der Funktion $p$ wird mit $G_{p}$ bezeichnet.

Untersuchen Sie, ob $G_{p}$ eine Symmetrie zum Koordinatensystem besitzt und geben Sie diese gegebenenfalls an.
Bestimmen Sie die Art der Definitionslücken von $p$ sowie die Koordinaten der Schnittpunkte von $G_{p}$ mit den Koordinatenachsen. Geben Sie auch für jede Asymptote des Graphen $G_{p}$ die Art und die Gleichung an.
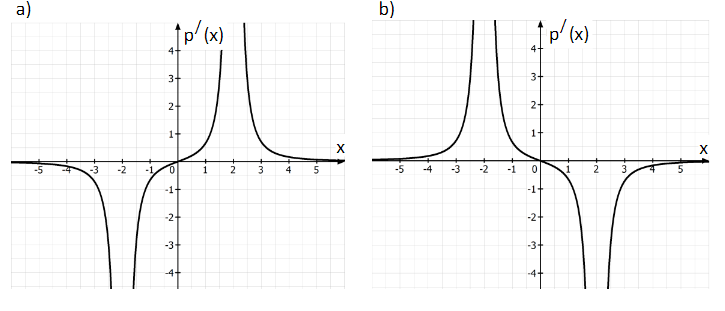
Eine der folgenden zwei Abbildungen zeigt den Graphen der ersten Ableitungsfunktion $p^{'}$ der Funktion $p$ . Nennen Sie den Buchstaben des richtigen Graphen und begründen Sie Ihre Wahl durch ein Argument.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?