Teil 1 Analysis

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgaben zum Ausdrucken als PDF findest du hier.

Die Aufgaben in diesem Ordner sollen ohne Hilfsmittel wie Taschenrechner oder Formelsammlung bearbeitet werden.

1
Gegeben ist die Funktion $p$ durch $p (x) = \frac{x^{2} - 1}{4 - x^{2}}$ mit ihrer maximalen Definitionsmenge $D_{p} = ℝ \ {- 2; 2}$ . Der Graph der Funktion $p$ wird mit $G_{p}$ bezeichnet.
1. Untersuchen Sie, ob $G_{p}$ eine Symmetrie zum Koordinatensystem besitzt und geben Sie diese gegebenenfalls an. (2 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Symmetrie von Graphen
  Untersuche, ob $G_{p}$ eine Symmetrie zum Koordinatensystem besitzt und gib diese gegebenenfalls an
  Prüfe $p (- x) = p (x)$ bzw. $p (- x) = - p (x)$ :
  $p (- x) = \frac{(- x)^{2} - 1}{4 - (- x)^{2}} = \frac{x^{2} - 1}{4 - x^{2}} = p (x) \Rightarrow$ $G_{p}$ ist symmetrisch zur y-Achse.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Prüfe $p (- x) = p (x)$ bzw. $p (- x) = - p (x)$ .
2. Bestimmen Sie die Art der Definitionslücken von $p$ sowie die Koordinaten der Schnittpunkte von $G_{p}$ mit den Koordinatenachsen. Geben Sie auch für jede Asymptote des Graphen $G_{p}$ die Art und die Gleichung an. (7 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Definitionsbereich bestimmen
  Bestimme die Art der Definitionslücken von $p$
  Gegeben ist $p (x) = \frac{x^{2} - 1}{4 - x^{2}} = \frac{x^{2} - 1}{(2 - x) \cdot (2 + x)}$ mit $D_{p} = ℝ \ {- 2; 2}$ .
  Die Definitionslücken sind $x = - 2$ und $x = 2$ . Es handelt sich um Polstellen ungerader Ordnung mit Vorzeichenwechsel.
  Bestimme die Koordinaten der Schnittpunkte von $G_{p}$ mit den Koordinatenachsen
  1. Schnittpunkte von $G_{p}$ mit der x-Achse:
  Berechne $p (x = 0) \Rightarrow 0 = x^{2} - 1 \Rightarrow x_{1,2} = \pm 1$
  $N_{1} (- 1 | 0)$ und $N_{2} (1 | 0)$ sind die Koordinaten der Schnittpunkte von $G_{p}$ mit der x-Achsen.
  2. Schnittpunkte von $G_{p}$ mit der y-Achse:
  Berechne $p (0) = \frac{0^{2} - 1}{4 - 0^{2}} = - \frac{1}{4} \Rightarrow S_{y} (0 | - \frac{1}{4})$
  Der Schnittpunkt von $G_{p}$ mit der y-Achse ist $S_{y} (0 | - \frac{1}{4})$ .
  Gib auch für jede Asymptote des Graphen $G_{p}$ die Art und die Gleichung an
  Senkrechte Asymptoten bei $x = - 2$ und bei $x = 2$ .
  Waagrechte Asymptote bei $y = - 1$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Teil 1
  Der Definitionsbereich zeigt Dir die Definitionslücken.
  Teil 2
  Für die Schnittpunkte von $G_{p}$ mit der x-Achse berechne $p (x) = 0$ .
  Für die Schnittpunkte von $G_{p}$ mit der y-Achse berechne $p (0)$ .
  Teil 3
  Wo gibt es senkrechte Asymptoten?
  Bestimme auch die Gleichung einer waagrechten Asymptote.
3. Eine der folgenden zwei Abbildungen zeigt den Graphen der ersten Ableitungsfunktion $p^{'}$ der Funktion $p$ . Nennen Sie den Buchstaben des richtigen Graphen und begründen Sie Ihre Wahl durch ein Argument. (3 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Graph einer Funktion
  Nenne den Buchstaben des richtigen Graphen
  Der Graph der ersten Ableitungsfunktion $p^{'}$ der Funktion $p$ gehört zu a).
  Begründe Deine Wahl durch ein Argument
  Berechne z.B. $p^{'} (x)$ mit der Quotientenregel und prüfe für einen x-Wert den Ableitungswert der Abbildung.
  $p^{'} (x) = \frac{(4 - x^{2}) \cdot 2 x - (x^{2} - 1) \cdot (- 2 x)}{(4 - x^{2})^{2}} = \frac{8 x - 2 x^{3} + 2 x^{3} - 2 x}{(4 - x^{2})^{2}} = \frac{6 x}{(4 - x^{2})^{2}}$
  Berechne z.B. die Ableitung an der Stelle $x = 1$ :
  $p^{'} (1) = \frac{6 \cdot 1}{(4 - 1^{2})^{2}} = \frac{6}{9} > 0$
  Betrachte die beiden Graphen, dann findest Du $p^{'} (1) = \frac{6}{9} > 0$ bei der Abbildung a).
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
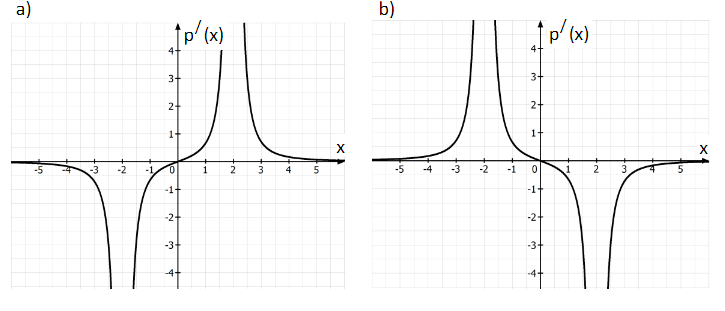
2
Gegeben ist die Funktion $f : x \to 2 x \cdot \ln (x + 3)$ mit ihrer maximalen Definitionsmenge $D_{f} =] - 3; \infty [$ .
1. Untersuchen Sie das Verhalten der Funktionswerte von $f$ an den Rändern der Definitionsmenge $D_{f}$ . (3 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Definitionsmenge
  Untersuche das Verhalten der Funktionswerte von $f$ an den Rändern der Definitionsmenge $D_{f}$
  Linker Rand:
  $\lim_{x \to - 3^{+}} \underset{\to - 6}{\underset{⏟}{2 x}} \cdot \underset{\to - \infty}{\underset{⏟}{\ln (x + 3)}} = + \infty$
  Rechter Rand:
  $\lim_{x \to \infty} \underset{\to \infty}{\underset{⏟}{2 x}} \cdot \underset{\to \infty}{\underset{⏟}{\ln (x + 3)}} = + \infty$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Betrachte das Verhalten von $f$ am linken Rand und am rechten Rand.
2. Ermitteln Sie die Nullstellen der Funktion $f$ . (3 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellen
  Ermittle die Nullstellen der Funktion $f$
  Berechne $f (x) = 0$ .
  $0 = 2 x \cdot \ln (x + 3)$
  Mit dem Satz vom Nullprodukt folgt:
  $2 x = 0 \Rightarrow x_{1} = 0$
  $\ln (x + 3) = 0 \Rightarrow x + 3 = 1 \Rightarrow x_{2} = - 2$
  Die Nullstellen der Funktion $f$ sind $x = 0$ und $x = - 2$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne $f (x) = 0$ .
3
Die Abbildung zeigt einen Ausschnitt des Graphen der Funktion $g : x \mapsto - e^{- 0,5 x} + e$ mit der Definitionsmenge $D_{g} = ℝ$ .
Die Funktion $G : x \to 2 e^{- 0,5 x} + e x$ mit der Definitionsmenge $D_{G} = ℝ$ ist eine Stammfunktion von $g$ (Nachweis nicht erforderlich). Berechnen Sie die Maßzahl des Inhalts des endlichen Flächenstücks, das der Graph von $g$ mit den Koordinatenachsen im zweiten Quadranten einschließt. (4 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
Berechne die Maßzahl des Inhalts des endlichen Flächenstücks, das der Graph von $g$ mit den Koordinatenachsen im zweiten Quadranten einschließt
Berechne zunächst die Nullstelle von $g$ :
$0$ $=$ $- e^{- 0,5 x} + e$ $+ e^{- 0,5 x}$
↓
Löse nach $x$ auf.
$e^{- 0,5 x}$ $=$ $e$ $\ln ()$
↓
$\ln e = 1$
$- 0,5 x$ $=$ $1$ $: (- 0,5)$
$x$ $=$ $- 2$
$x = - 2$ ist die untere Integrationsgrenze und $x = 0$ ist die obere Integrationsgrenze.
Dann folgt mit der gegebenen Stammfunktion:
$A = \int_{- 2}^{0} (- e^{- 0,5 x} + e) d x = {[2 e^{- 0,5 x} + e x]}_{- 2}^{0} = (2 e^{0} + 0) - (2 e^{1} - 2 e) = 2$
Die Maßzahl des Inhalts des endlichen Flächenstücks, das der Graph von $g$ mit den Koordinatenachsen im zweiten Quadranten einschließt, beträgt $2 FE$ .
Berechne die Nullstelle von $g$ $\Rightarrow x_{1}$ .
$x_{1}$ ist die untere Integrationsgrenze und $x = 0$ ist die obere Integrationsgrenze.
Berechne mit der gegebenen Stammfunktion $A = \int_{x_{1}}^{0} (- e^{- 0,5 x} + e) d x$ .

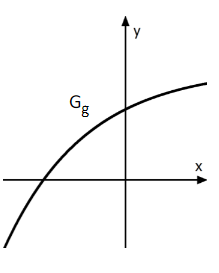
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$0$	$=$	$- e^{- 0,5 x} + e$	$+ e^{- 0,5 x}$
	↓	Löse nach $x$ auf.
$e^{- 0,5 x}$	$=$	$e$	$\ln ()$
	↓	$\ln e = 1$
$- 0,5 x$	$=$	$1$	$: (- 0,5)$
$x$	$=$	$- 2$

Teil 1 Analysis

Untersuche, ob Gp eine Symmetrie zum Koordinatensystem besitzt und gib diese gegebenenfalls an

Hast du eine Frage oder Feedback?

Bestimme die Art der Definitionslücken von p

Bestimme die Koordinaten der Schnittpunkte von Gp mit den Koordinatenachsen

Gib auch für jede Asymptote des Graphen Gp die Art und die Gleichung an

Hast du eine Frage oder Feedback?

Nenne den Buchstaben des richtigen Graphen

Begründe Deine Wahl durch ein Argument

Hast du eine Frage oder Feedback?

Untersuche das Verhalten der Funktionswerte von f an den Rändern der Definitionsmenge Df

Hast du eine Frage oder Feedback?

Ermittle die Nullstellen der Funktion f

Hast du eine Frage oder Feedback?

Berechne die Maßzahl des Inhalts des endlichen Flächenstücks, das der Graph von g mit den Koordinatenachsen im zweiten Quadranten einschließt

Untersuche, ob $G_{p}$ eine Symmetrie zum Koordinatensystem besitzt und gib diese gegebenenfalls an

Bestimme die Art der Definitionslücken von $p$

Bestimme die Koordinaten der Schnittpunkte von $G_{p}$ mit den Koordinatenachsen

Gib auch für jede Asymptote des Graphen $G_{p}$ die Art und die Gleichung an

Untersuche das Verhalten der Funktionswerte von $f$ an den Rändern der Definitionsmenge $D_{f}$

Ermittle die Nullstellen der Funktion $f$

Berechne die Maßzahl des Inhalts des endlichen Flächenstücks, das der Graph von $g$ mit den Koordinatenachsen im zweiten Quadranten einschließt