Teil 2 Lineare Algebra und analytische Geometrie I

Das Zelt eines Jugendzirkus weist die Form eines regelmäßigen Prismas mit aufgesetzter Pyramide auf und wird modellhaft in einem kartesischen Koordinatensystem des $\mathbb{R^3}$ betrachtet. Die Grundfläche des Zeltes liegt in der $x_{1}$ - $x_{2}$ -Koordinatenebene und ist ein regelmäßiges Sechseck $O A B C D E$ mit dem Mittelpunkt $M(3| 3\sqrt{ 3}| 0)$ . Die Seiten des Sechsecks sind jeweils $6 m$ lang. Der Punkt $O$ liegt im Koordinatenursprung, $A$ hat die Koordinaten $(6 ∣ 0 ∣ 0)$ und $A_{1}$ die Koordinaten $(6 ∣ 0 ∣ 4)$ . Das Dach des Zeltes wird durch eine regelmäßige sechseckige Pyramide gebildet. Die Spitze S des Zeltes liegt senkrecht über $M$ in einer Höhe von $6 m$ . Die Koordinaten sind Längenangaben in der Einheit Meter. Auf die Mitführung von Einheiten während der Rechnungen kann verzichtet werden. Die Ergebnisse sind sinnvoll zu runden.

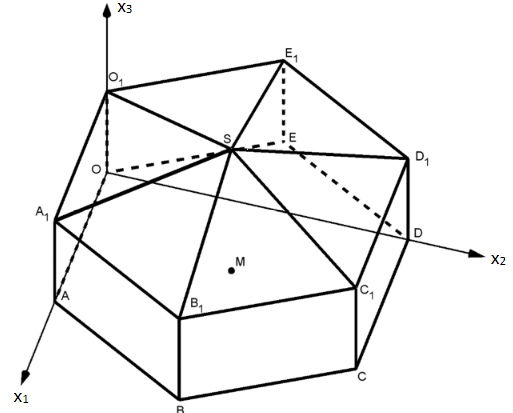
Zusätzlich zeigt die folgende Zeichnung den Grundriss des Zeltes in der $x_{1}$ - $x_{2}$ -Ebene.

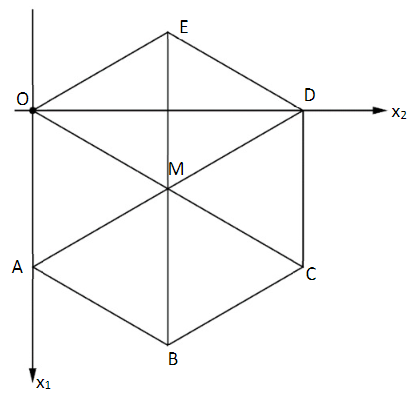
Ermitteln Sie die Koordinaten der Eckpunkte $B$ , $C$ und $C_{1} .$
Für das Zelt und die Zirkuswagen wird eine Stellfläche benötigt, die $2,5$ -mal so groß ist wie die Grundfläche des Zirkuszeltes. Ein Landwirt stellt dem Zirkus eine Wiese mit einer Fläche von $240\ m²$ zur Verfügung. Prüfen Sie, ob diese Fläche groß genug ist.
[ Teilergebnis: $A_{Zelt}\approx 93{,}5\m^2$ ]
Bestimmen Sie eine Gleichung der Ebene $F$ in Koordinatenform, welche durch die Punkte $O_{1} (0 ∣ 0 ∣ 4)$ , $E_1(-3| 3\sqrt{ 3}| 4)$ und $S(3| 3\sqrt{ 3}| 6)$ festgelegt wird.
[ Mögliches Ergebnis: $F:x_1+\dfrac{\sqrt{3}}{3}x_2+3x_3=-12$ ]
Berechnen Sie den Neigungswinkel der Ebene $F$ aus Teilaufgabe 1.c gegenüber der Grundfläche des Zeltes.
Vom Schwerpunkt $S P$ des Dreiecks $O_{1} S E_{1}$ soll senkrecht zur Ebene $F$ ein Drahtseil bis zum Boden gespannt werden. Berechnen Sie die Länge dieses Seils.
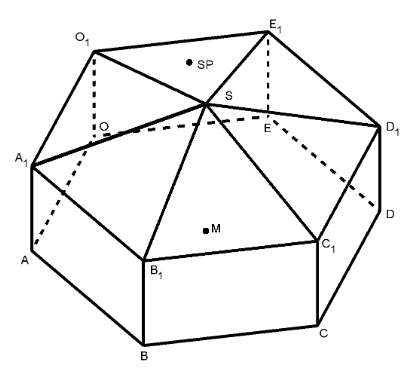
Zur Abendvorstellung soll ein Lichtstrahl auf die Seitenfläche $O A A_{1} O_{1}$ , in der sich auch der Eingang befindet, treffen. Dazu wird auf einem Mast ein Spotlight installiert, dessen Lichtstrahl durch $h:\overrightarrow x=\begin{pmatrix} 2 \\ -4\\ 10 \end{pmatrix}+s\cdot \begin{pmatrix} 3 \\ 4 \\ -5 \end{pmatrix}$ mit $s\in \mathbb{R^+}$ beschrieben wird. Prüfen Sie, ob der Lichtstrahl des Spotlights die Seitenfläche $O A A_{1} O_{1}$ trifft. Geben Sie gegebenenfalls an, wie die Position des Spotlights am Mast verändert werden muss, damit die gewünschte Beleuchtung erzielt wird, wenn der Lichtstrahl nach wie vor parallel zu $h$ verlaufen soll.