Springe zum Inhalt oder Footer
SerloDie freie Lernplattform

Apfelbauer AP\text{AP}, Birnenbauer BI\text{BI}, Kirschenbauer KI\text{KI} und Erdbeerbauer ER\text{ER} sind vier Obstbauern vom Bodensee, die untereinander die Obstsorten tauschen, um jeweils in ihrem Hofladen den Kunden verschiedene, gemischte Obstkisten anbieten zu können.

  1. Die vier Bauern sind untereinander und mit dem Markt nach dem Leontief-Modell verbunden. Die Inputmatrix ist

    A=(0,60,10,050,050,070,700,030,10,10,30,10,20,050,150,5)A = \begin{pmatrix} 0{,}6 & 0{,}1 & 0{,}05 & 0{,}05 \\ 0{,}07 & 0{,}7 & 0 & 0{,}03 \\ 0{,}1 & 0{,}1 & 0{,}3 & 0{,}1 \\ 0{,}2 & 0{,}05 & 0{,}15 & 0{,}5\end{pmatrix}

    Die Gesamtproduktion von KI\text{KI} beträgt 200200 ME (Mengeneinheiten), diejenige von ER\text{ER} 600600 ME. Übertragen Sie das Verflechtungsdiagramm (siehe unten) auf Ihren Bearbeitungsbogen, berechnen Sie alle fehlenden Zahlenwerte und tragen Sie diese in Ihr Diagramm ein.

    Bild

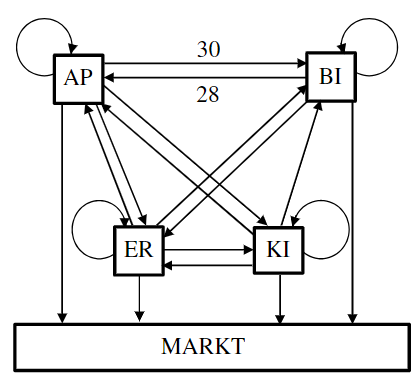
  2. Nach der Erdbeer-Saison steigt Bauer ER\text{ER} aus dem gemeinsamen Tausch aus, während APAP, BIBI und KIKI weiter zusammenarbeiten. Für die neue, veränderte Inputmatrix AA* gilt: AA*= (0,60,10,050,070,7000,10,3)\begin{pmatrix} 0{,}6 & 0{,}1 & 0{,}05 \\ 0{,}07 & 0{,}7 & 0 \\ 0 & 0{,}1 & 0{,}3 \end{pmatrix}

    (1) Die Produktionszahlen ändern sich zum Saisonende und werden durch den Produktionsvektor x⃗=(700+2k600150−k)\vec{x} = \begin{pmatrix} 700+2k \\ 600 \\ 150-k \end{pmatrix} mit k∈R0+k\in \mathbb{R}_0^+ dargestellt. Berechnen Sie die Produktionsmengen der Bauern, wenn BI\text{BI} 124124 ME an den Markt abgibt.

    (2) Nach strukturellen Veränderungen in den Betrieben kalkulieren die Bauern AP\text{AP}, BI\text{BI} und KI\text{KI} für die kommende Saison eine Marktabgabe von 351351 ME an Äpfeln, 157157 ME Birnen und 7676 ME Kirschen. Bestimmen Sie die Mengen an Obst, die die Bauern bei gleichbleibender Verflechtung jeweils produzieren müssten, um die Konsummengen zu erreichen.