Geben Sie die besondere Lage der Geraden $g_a$ im Koordinatensystem in Abhängigkeit von $a$ an.

Untersuchen Sie die gegenseitige Lage der Geraden $g_a$ und $h$ in Abhängigkeit von $a$ und geben Sie gegebenenfalls die Koordinaten des Schnittpunktes $P$ an.

Für $a=-2$ wird die Ebene $E$ durch die Gerade $g_{-2}$ und den Punkt $B$ festgelegt, welcher nicht auf $g_{-2}$ liegt (Nachweis nicht erforderlich!).

1. Bestimmen Sie je eine Parameter- und eine Koordinatengleichung der Ebene $E$.

[ Mögliches Ergebnis: $E:x_1+2x_2+2x_3\text{–}3=0$ ]

2. Zeigen Sie, dass die Gerade $h$ in der Ebene $E$ liegt.

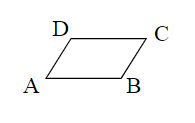
3. Fertigen Sie eine Skizze an, aus der die gegenseitige Lage der Ebene $E$, der Geraden

$g_{-2}$ und $h$ sowie der Punkte $A,B$ und $P$ erkennbar ist. Verwenden Sie kein

Koordinatensystem.

4. Die Punkte $A,B,C(3|0|0)$ und $D(d_1|d_2|d_3)$ bilden ein Parallelogramm (siehe Skizze).

Bestimmen Sie die Koordinaten von $D$ und überprüfen Sie, ob das Parallelogramm

$ABCD$ in der Ebene $E$ liegt.